Công thức tính parabol và hướng dẫn xác định đặc điểm và ứng dụng trong toán học

Công thức tính parabol là công cụ quan trọng giúp học sinh xác định đặc điểm và hình dạng của parabol trong toán học. Bài viết này sẽ cung cấp kiến thức cơ bản, phương pháp xác định đỉnh, trục đối xứng và cách vẽ đồ thị parabol một cách chính xác.

Công thức tính parabol và các thành phần cơ bản

Công thức tính công thức tính parabol chuẩn có dạng y = ax² + bx + c, trong đó a, b, c là các hệ số và a ≠ 0. Hệ số a quyết định hướng mở của parabol – nếu a > 0 thì parabol mở lên trên, nếu a < 0 thì parabol mở xuống dưới. Đây là dạng tổng quát được sử dụng phổ biến nhất trong toán học.

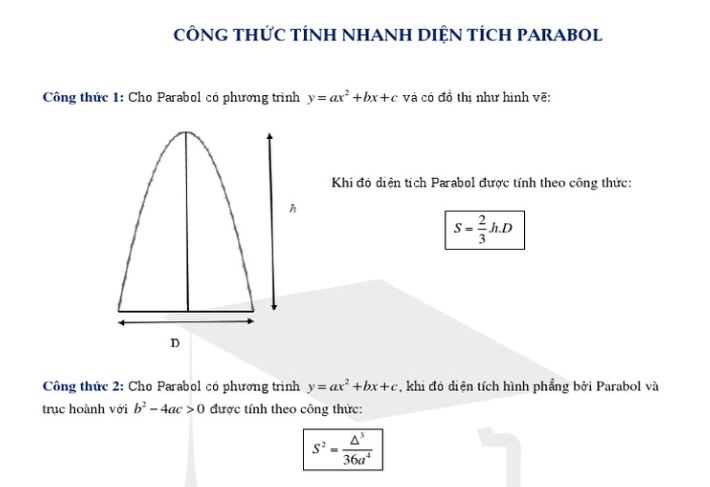
Để xác định các thành phần quan trọng của parabol, ta cần chú ý đến tọa độ đỉnh và trục đối xứng. Tọa độ đỉnh được tính theo công thức: x = -b/(2a) và y = -Δ/(4a), trong đó Δ = b² – 4ac là định thức của phương trình parabol. Trục đối xứng của parabol là đường thẳng song song với trục Oy và đi qua đỉnh của parabol.

Khi áp dụng phương trình parabol vào thực tế, ta thường gặp các bài toán liên quan đến chuyển động của vật thể, quỹ đạo của các hành tinh, hay thiết kế các công trình kiến trúc. Ví dụ như cầu vòm, đèn pha ô tô hay ăng-ten parabol đều được thiết kế dựa trên nguyên lý của đường parabol để tối ưu hóa hiệu suất sử dụng.

Đặc điểm và tính chất quan trọng của đường parabol trong toán học

Đường parabol là một trong những đối tượng hình học cơ bản và quan trọng trong toán hình học phẳng. Các đặc điểm parabol thể hiện qua hình dạng đặc trưng và những tính chất độc đáo của nó trong không gian hai chiều.

Đường cong này có vai trò quan trọng không chỉ trong toán học thuần túy mà còn trong nhiều ứng dụng thực tiễn như thiết kế kiến trúc, quang học và vật lý. Tính chất parabol đặc biệt giúp nó trở thành công cụ hữu ích trong việc mô tả các hiện tượng tự nhiên và giải quyết các bài toán thực tế.

Định nghĩa và đặc điểm hình học của parabol

Parabol là tập hợp các điểm trong mặt phẳng có khoảng cách đến một điểm cố định (tiêu điểm) bằng khoảng cách đến một đường thẳng cố định (đường chuẩn). Đặc điểm này tạo nên hình dạng đối xứng đặc trưng của parabol.

Trục đối xứng của parabol đi qua tiêu điểm và vuông góc với đường chuẩn. Đỉnh của parabol là điểm nằm trên trục đối xứng và có khoảng cách đến tiêu điểm bằng khoảng cách đến đường chuẩn.

Parabol trong toán học còn được đặc trưng bởi tham số p gọi là thông số của parabol, là khoảng cách từ tiêu điểm đến đường chuẩn. Giá trị này quyết định độ mở của parabol.

Các tính chất đặc trưng của đường parabol

Tính chất phản xạ là một trong những đặc điểm nổi bật nhất của parabol. Các tia sáng song song với trục đối xứng khi chiếu vào parabol sẽ phản xạ qua tiêu điểm. Nguyên lý này được ứng dụng rộng rãi trong thiết kế đèn pha ô tô và ăng-ten parabol.

Theo nghiên cứu của Viện Khoa học và Công nghệ Việt Nam, tính chất này được ứng dụng hiệu quả trong việc thu và phát sóng vô tuyến, giúp tăng cường độ tín hiệu đáng kể so với các dạng ăng-ten thông thường.

Parabol còn có tính chất đối xứng qua trục chính, điều này giúp đơn giản hóa việc tính toán và phân tích trong nhiều bài toán thực tế.

Mối quan hệ giữa parabol và hàm bậc hai

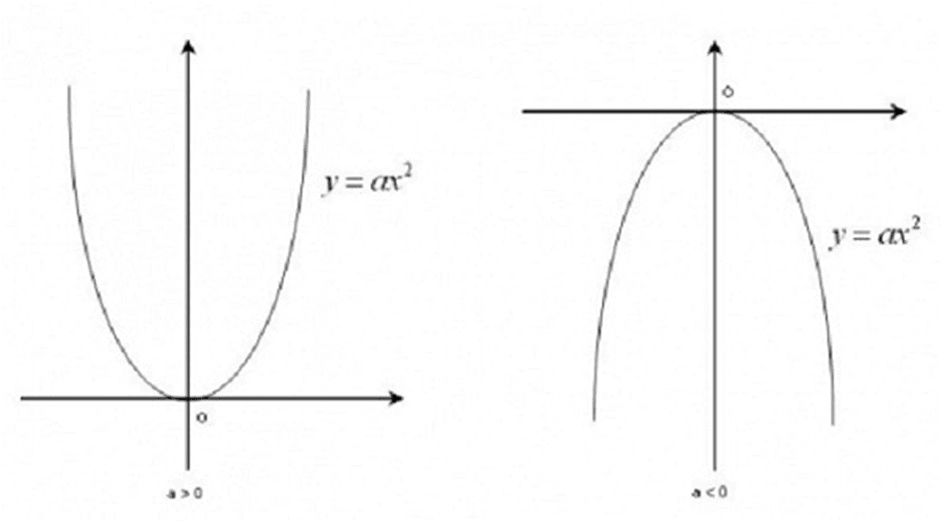
Mối liên hệ giữa parabol và hàm bậc hai thể hiện qua đồ thị của hàm số y = ax² + bx + c. Khi a ≠ 0, đồ thị của hàm số luôn là một parabol với trục đối xứng song song với trục tung.

Dấu của hệ số a quyết định chiều mở của parabol. Khi a > 0, parabol mở lên trên và khi a < 0, parabol mở xuống dưới. Giá trị tuyệt đối của a ảnh hưởng đến độ “béo” hay “gầy” của parabol.

Các hệ số b và c có vai trò quan trọng trong việc xác định vị trí của parabol trên mặt phẳng tọa độ. Hệ số b ảnh hưởng đến sự dịch chuyển ngang, trong khi c quyết định điểm cắt của parabol với trục tung.

Hướng dẫn xác định đỉnh và trục đối xứng của parabol

Để xác định chính xác vị trí đỉnh và trục đối xứng của parabol, cần nắm vững các công thức và phương pháp phân tích hình học. Việc xác định các yếu tố này giúp phân tích được đặc điểm và hình dạng của đồ thị hàm số bậc hai một cách toàn diện.

Công thức tính toạ độ đỉnh parabol

Công thức tính đỉnh parabol được xác định thông qua hệ số của phương trình bậc hai y = ax² + bx + c. Với hoành độ đỉnh x = -b/2a và tung độ đỉnh y = -Δ/4a (trong đó Δ = b² – 4ac là định thức của phương trình). Công thức này áp dụng cho mọi parabol, bất kể hướng mở lên hay mở xuống.

Việc áp dụng công thức cần chú ý đến dấu của các hệ số, đặc biệt là hệ số a quyết định chiều mở của parabol. Khi a > 0, parabol mở lên và đỉnh là điểm thấp nhất. Ngược lại khi a < 0, parabol mở xuống và đỉnh là điểm cao nhất.

Phương pháp xác định trục đối xứng

Trục đối xứng của parabol là đường thẳng đi qua đỉnh và vuông góc với trục hoành. Phương trình trục đối xứng có dạng x = -b/2a, trùng với hoành độ của đỉnh. Để xác định trục đối xứng, có thể sử dụng công thức tính đường sinh kết hợp với tính chất đối xứng.

Một cách thực tế để kiểm tra trục đối xứng là lấy hai điểm bất kỳ cách đều trục và có cùng tung độ. Điều này giúp xác minh tính đối xứng của parabol qua trục đã tìm được.

Ý nghĩa hình học của đỉnh parabol

Đỉnh parabol là điểm đặc biệt thể hiện giá trị cực trị của hàm số bậc hai. Về mặt hình học, đây là điểm mà tại đó tiếp tuyến của parabol song song với trục hoành. Điểm này cũng là giao điểm duy nhất của parabol với trục đối xứng.

Trong ứng dụng thực tế, đỉnh parabol có vai trò quan trọng trong việc tối ưu hóa các bài toán thực tế như tính toán quỹ đạo chuyển động của vật, thiết kế các công trình kiến trúc hay xác định điểm cao nhất/thấp nhất trong các bài toán tối ưu.

Ngoài ra, đỉnh parabol còn được sử dụng để phân tích tính chất đối xứng và dự đoán hình dạng của đồ thị, giúp việc khảo sát hàm số trở nên thuận tiện và chính xác hơn.

Phương pháp vẽ đồ thị parabol chính xác

Để vẽ được đồ thị parabol một cách chính xác, việc nắm vững các phương pháp và kỹ thuật vẽ là vô cùng quan trọng. Cách vẽ parabol chuẩn xác đòi hỏi sự tỉ mỉ trong từng bước thực hiện, từ việc xác định các điểm đặc trưng đến kỹ thuật nối các điểm với nhau.

Việc vẽ đồ thị hình parabola không chỉ đơn thuần là nối các điểm một cách máy móc mà cần tuân theo các nguyên tắc toán học nhất định. Tương tự như công thức bán kính mặt cầu, việc áp dụng đúng công thức và quy tắc sẽ giúp đồ thị được vẽ chính xác.

Các bước vẽ parabol cơ bản

Bước đầu tiên là xác định hệ trục tọa độ Oxy và đơn vị đo trên mỗi trục. Việc chọn tỷ lệ phù hợp giúp đồ thị được vẽ cân đối và dễ quan sát.

Tiếp theo, cần xác định dạng phương trình của parabol để biết được hướng mở của đồ thị. Nếu hệ số của x² dương, parabol mở lên trên. Ngược lại, nếu hệ số âm, parabol mở xuống dưới.

Sau khi có phương trình, ta thay các giá trị x vào để tính toán các điểm tương ứng trên đồ thị. Nên chọn các giá trị x đối xứng qua trục đối xứng của parabol để việc vẽ được cân đối.

Xác định điểm đặc biệt trên đồ thị

Đỉnh của parabol là điểm quan trọng nhất cần xác định chính xác. Đây là điểm cao nhất (với parabol mở xuống) hoặc thấp nhất (với parabol mở lên) của đồ thị.

Giao điểm với trục hoành được tìm bằng cách giải phương trình bậc hai khi y = 0. Các điểm này giúp xác định vị trí cắt trục x của parabol.

Giao điểm với trục tung được xác định bằng cách thế x = 0 vào phương trình. Điểm này cho biết vị trí parabol cắt trục y.

Kỹ thuật vẽ parabol nâng cao

Để vẽ parabol mượt mà, ta nên chia nhỏ khoảng cách giữa các điểm đã tính được. Việc này giúp đường cong được vẽ liền mạch và tự nhiên hơn.

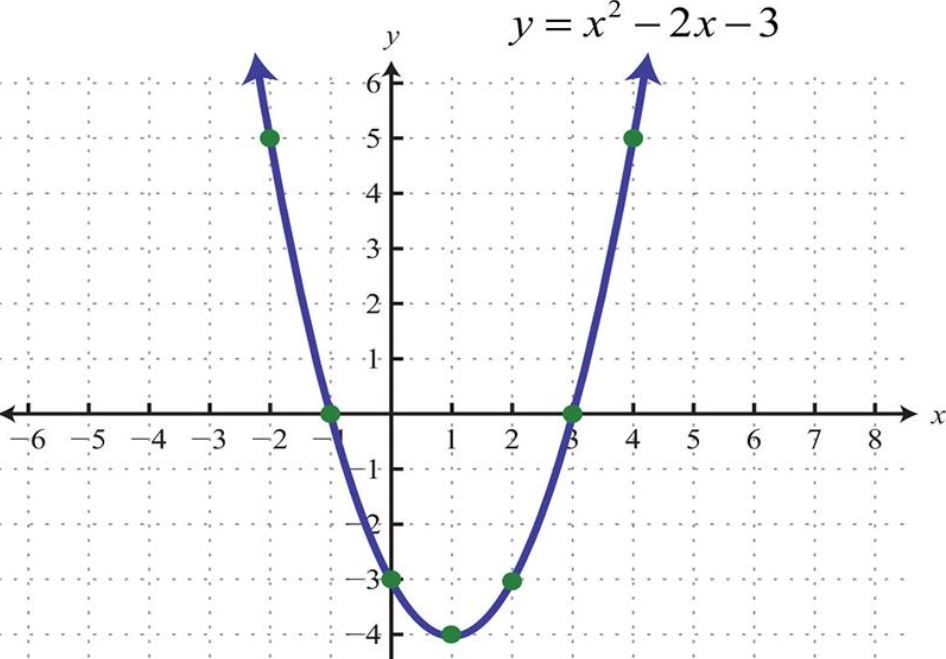
Sử dụng tính chất đối xứng của parabol qua trục đối xứng giúp việc vẽ nhanh và chính xác hơn. Khi vẽ xong một nửa parabol, ta có thể lấy đối xứng để hoàn thành nửa còn lại.

Khi nối các điểm, cần chú ý đến độ cong của đường vẽ. Độ cong phải thay đổi từ từ và đều đặn, không được gấp khúc hoặc thay đổi đột ngột. Việc sử dụng thước cong chuyên dụng sẽ giúp đường vẽ mượt mà và chuyên nghiệp hơn.

Ứng dụng thực tiễn của parabol và cách tìm nghiệm

Parabol có nhiều ứng dụng quan trọng trong thực tế, từ thiết kế kiến trúc đến tính toán quỹ đạo chuyển động. Việc hiểu rõ cách tìm nghiệm và ứng dụng công thức tính parabol giúp giải quyết nhiều bài toán thực tiễn một cách hiệu quả.

Trong lĩnh vực tài chính, parabol được áp dụng để mô phỏng sự tăng trưởng của các khoản đầu tư theo công thức tính lãi xuất. Các chuyên gia tại Hocthenao.vn đã chỉ ra rằng đường cong parabol thể hiện chính xác mối quan hệ giữa lợi nhuận và thời gian trong nhiều trường hợp.

Các bài toán thực tế liên quan đến parabol

Trong xây dựng, ứng dụng parabol được thể hiện rõ nét qua thiết kế cầu treo, mái vòm và các công trình kiến trúc. Ví dụ điển hình là cầu cảng Sydney với thiết kế dây cáp theo đường parabol, tạo nên sự cân bằng và độ bền vững cho công trình.

Ngành thể thao cũng áp dụng parabol để phân tích quỹ đạo chuyển động của bóng. Các huấn luyện viên bóng đá chuyên nghiệp sử dụng phần mềm mô phỏng dựa trên phương trình parabol để tối ưu góc sút và lực đá cho cầu thủ.

Phương pháp tìm nghiệm của phương trình bậc hai

Việc tìm nghiệm của parabol có thể thực hiện qua nhiều phương pháp khác nhau. Phương pháp phổ biến nhất là sử dụng công thức nghiệm tổng quát, áp dụng cho mọi phương trình bậc hai dạng ax² + bx + c = 0.

Phương pháp đồ thị cũng được sử dụng rộng rãi, đặc biệt khi cần trực quan hóa vị trí nghiệm. Điểm cắt của đường parabol với trục hoành chính là nghiệm của phương trình.

Ngoài ra, phương pháp phân tích thành nhân tử thường được áp dụng khi hệ số của phương trình là số nguyên, giúp đơn giản hóa quá trình tính toán và kiểm tra kết quả.

Ứng dụng parabol trong khoa học và kỹ thuật

Trong vật lý học, parabol đóng vai trò quan trọng trong nghiên cứu chuyển động của vật trong trường trọng lực. NASA sử dụng các tính toán dựa trên quỹ đạo parabol để thiết kế tên lửa và dự đoán đường bay của các vật thể không gian.

Ngành quang học ứng dụng parabol trong thiết kế gương phản xạ và ăng-ten vệ tinh. Các kỹ sư tại Đài thiên văn Arecibo đã thiết kế bề mặt phản xạ parabol khổng lồ để thu nhận tín hiệu vô tuyến từ vũ trụ.

Lĩnh vực công nghệ năng lượng mặt trời cũng tận dụng đặc tính phản xạ của parabol. Các tấm pin mặt trời được thiết kế theo dạng parabol để tập trung ánh sáng mặt trời, nâng cao hiệu suất thu năng lượng lên đến 40%.

Khi nghiên cứu về công thức tính parabol, bạn sẽ khám phá nhiều khía cạnh quan trọng như đặc điểm, tính chất và ứng dụng của loại hình toán học này. Việc hiểu rõ về đỉnh, trục đối xứng và phương pháp vẽ đồ thị parabol sẽ hỗ trợ bạn giải quyết các bài toán phức tạp hơn. Với các kiến thức này, bạn hoàn toàn có thể tự tin áp dụng vào thực tiễn và nâng cao khả năng tư duy toán học của mình.