Phương trình parabol và cách viết, áp dụng hiệu quả trong toán học

Phương trình parabol là một trong những khái niệm quan trọng trong toán học. Bài viết sẽ hướng dẫn bạn các đặc điểm cơ bản, cách viết phương trình parabol và ứng dụng của nó trong giải bài tập. Tìm hiểu những nguyên tắc và công thức cụ thể để vận dụng hiệu quả trong mọi tình huống học tập.

Phương trình parabol và các đặc điểm cơ bản trong toán học

Phương trình parabol là một dạng phương trình bậc hai có dạng y = ax² + bx + c, trong đó a ≠ 0. Đây là một trong những phương trình quan trọng trong toán học, thường được sử dụng để mô tả các hiện tượng vật lý như chuyển động của vật trong trường hấp dẫn hoặc quỹ đạo của các vật thể trong không gian.

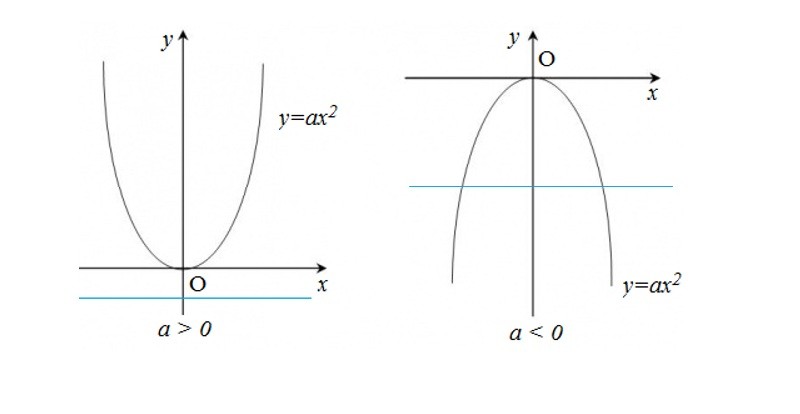
Khi vẽ đồ thị, phương trình parabol có dạng đường cong đối xứng qua một trục thẳng đứng. Tùy thuộc vào giá trị của hệ số a, parabol có thể mở rộng lên trên (a > 0) hoặc mở rộng xuống dưới (a < 0). Điều này được ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, kỹ thuật và thiết kế. Theo Hocthenao.vn, việc hiểu rõ các tính chất của parabol giúp học sinh nắm vững kiến thức toán học và áp dụng hiệu quả vào thực tế.

Đặc điểm nổi bật của parabol là sự tồn tại của đỉnh – điểm cao nhất hoặc thấp nhất của đường cong. Đỉnh này có tọa độ x = -b/(2a) và y = -Δ/(4a), trong đó Δ là định thức của phương trình. Ngoài ra, parabol còn có trục đối xứng đi qua đỉnh và song song với trục tung, tạo nên tính đối xứng hoàn hảo cho đường cong.

Dạng tổng quát và phương trình chính tắc của đường parabol

Phương trình chính tắc của parabol là dạng phương trình đơn giản nhất mô tả đường parabol, được biểu diễn dưới dạng chuẩn hóa sau khi đã chuyển hệ trục tọa độ. Phương trình tổng quát có dạng ax² + bxy + cy² + dx + ey + f = 0, trong đó b² – 4ac = 0.

Để thuận tiện trong việc khảo sát tính chất và vẽ đồ thị, ta thường chuyển từ phương trình tổng quát sang công thức tính parabol. Việc này giúp xác định rõ các yếu tố hình học quan trọng như tiêu điểm, đỉnh và trục đối xứng.

Các dạng phương trình chính tắc parabol thường gặp

Phương trình chính tắc parabol có 4 dạng cơ bản tùy thuộc vào hướng mở của parabol. Khi parabol mở lên trên hoặc xuống dưới, phương trình có dạng x = ±ay². Với parabol mở sang trái hoặc phải, phương trình có dạng y = ±ax².

Các dạng này được xây dựng dựa trên định nghĩa hình học của parabol – tập hợp các điểm cách đều một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn). Mỗi dạng thể hiện một hướng mở khác nhau của đường cong.

Cách chuyển từ phương trình tổng quát sang phương trình chính tắc

Quá trình chuyển đổi từ phương trình tổng quát sang phương trình chính tắc thực hiện qua các bước: hoàn chỉnh bình phương, tách nhóm các số hạng chứa x và y, đưa về dạng tổng/hiệu các bình phương hoàn chỉnh.

Việc chuyển đổi này đòi hỏi kỹ năng tính toán và biến đổi đại số thành thạo. Kết quả cuối cùng sẽ cho ta một phương trình ở dạng chuẩn, từ đó dễ dàng xác định các yếu tố hình học của parabol.

Ý nghĩa hình học của các tham số trong phương trình

Các tham số trong phương trình chính tắc mang những ý nghĩa hình học quan trọng. Hệ số a quyết định độ mở rộng của parabol – |a| càng nhỏ thì parabol càng mở rộng, dấu của a xác định hướng mở.

Tọa độ đỉnh (h,k) cho biết vị trí của điểm đỉnh parabol trong mặt phẳng tọa độ. Trục đối xứng của parabol song song với trục tọa độ và đi qua đỉnh. Khoảng cách từ tiêu điểm đến đường chuẩn bằng 2p, với p là tham số của parabol.

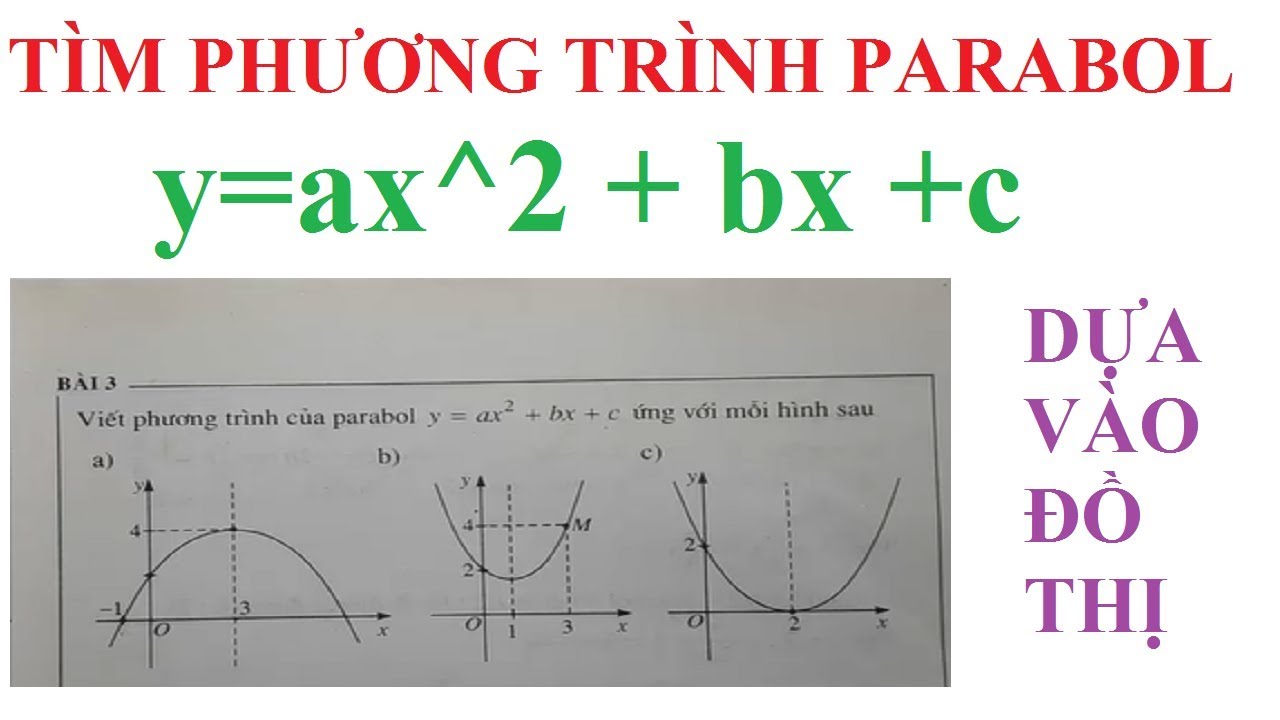
Hiểu rõ ý nghĩa của các tham số giúp ta dễ dàng vẽ đồ thị và phân tích các tính chất hình học của parabol một cách trực quan.

Hướng dẫn viết phương trình parabol từ các yếu tố cho trước

Để viết phương trình parabol chính xác, việc nắm vững các yếu tố cơ bản và quy trình thực hiện là rất quan trọng. Phương trình parabol có dạng tổng quát y = ax² + bx + c, trong đó các hệ số a, b, c quyết định hình dạng và vị trí của đường cong.

Khi xác định phương trình của parabol, cần phân tích kỹ các thông tin đã cho về đường cong. Các yếu tố quan trọng bao gồm tọa độ đỉnh, hướng mở và điểm đi qua. Việc phân tích này giúp xác định chính xác dạng phương trình cần sử dụng.

Xác định tọa độ đỉnh và trục đối xứng

Tọa độ đỉnh (h,k) là yếu tố then chốt để viết phương trình parabol dạng đỉnh y = a(x-h)² + k. Đỉnh là điểm cao nhất hoặc thấp nhất của parabol, tùy thuộc vào hướng mở.

Trục đối xứng của parabol là đường thẳng đi qua đỉnh và vuông góc với trục hoành. Với parabol có đỉnh (h,k), trục đối xứng có phương trình x = h. Việc xác định chính xác trục đối xứng giúp kiểm tra tính đúng đắn của phương trình.

Trong nhiều trường hợp phức tạp, có thể áp dụng giải hệ phương trình bằng phương pháp gauss để tìm tọa độ đỉnh từ các điểm đã biết.

Xác định hệ số và hướng mở của parabol

Hệ số a trong phương trình parabol quyết định độ mở rộng và hướng mở của đường cong. Khi |a| lớn, parabol có độ mở hẹp và ngược lại. Dấu của a xác định hướng mở: a > 0 mở lên trên, a < 0 mở xuống dưới.

Để xác định giá trị của a, cần sử dụng một điểm đã biết nằm trên parabol. Thay tọa độ điểm này vào phương trình dạng đỉnh sẽ cho phương trình xác định a.

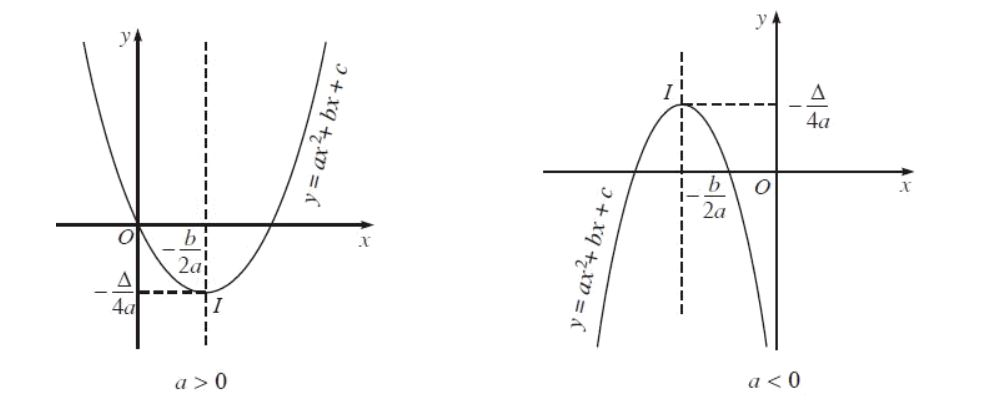
Việc xác định chính xác hệ số a rất quan trọng vì nó ảnh hưởng trực tiếp đến hình dạng của parabol. Một sai số nhỏ trong tính toán có thể dẫn đến sự khác biệt lớn về hình dạng đường cong.

Các bước viết phương trình parabol chuẩn

Bước 1: Xác định tọa độ đỉnh (h,k) từ các thông tin cho trước.
Bước 2: Viết phương trình dạng đỉnh y = a(x-h)² + k.
Bước 3: Sử dụng điểm đã biết để tìm hệ số a.
Bước 4: Thay a vào phương trình để có dạng hoàn chỉnh.

Quá trình này đảm bảo phương trình thu được chính xác và phản ánh đúng các đặc điểm của parabol. Sau khi hoàn thành, nên kiểm tra lại bằng cách thế các điểm đã biết vào phương trình.

Việc thực hiện theo trình tự các bước giúp tránh sai sót và đảm bảo kết quả chính xác. Mỗi bước đều quan trọng và không thể bỏ qua hoặc thực hiện không đúng thứ tự.

Phương trình đường chuẩn của parabol và ứng dụng trong giải toán

Đường parabol là một đường cong bậc hai có dạng chuẩn tắc được xác định bởi tập hợp các điểm có khoảng cách đến một điểm cố định (tiêu điểm) bằng khoảng cách đến một đường thẳng cố định (đường chuẩn). Phương trình đường chuẩn của parabol thường được biểu diễn dưới dạng y = ax² hoặc x = ay², trong đó a là một hằng số khác 0.

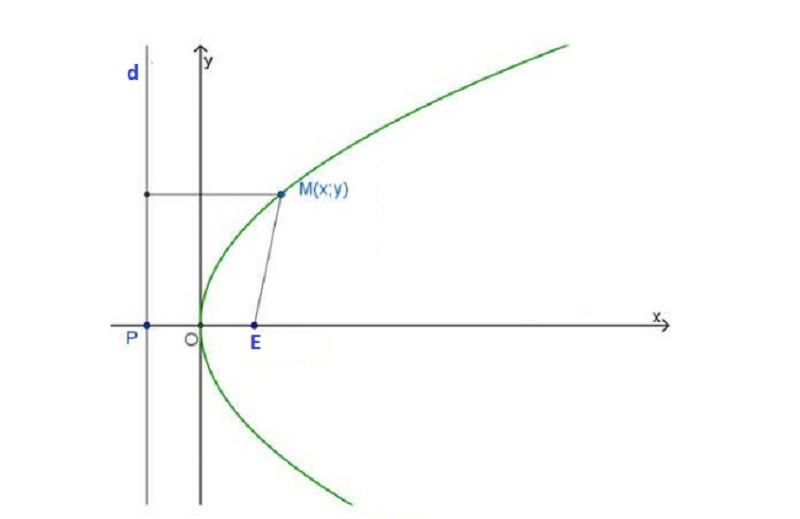
Việc nắm vững các dạng phương trình này giúp giải quyết nhiều bài toán trong hình học giải tích và ứng dụng thực tế như thiết kế đèn pha ô tô, ăng-ten parabol hay các công trình kiến trúc. Đặc biệt, parabol có mối liên hệ chặt chẽ với các phương trình đường tròn và phương trình đường elip trong họ đường conic.

Các dạng đường chuẩn của parabol

Đường chuẩn của parabol có thể được biểu diễn theo nhiều dạng khác nhau tùy thuộc vào vị trí của trục đối xứng và hướng mở của parabol. Dạng cơ bản nhất là parabol có trục đối xứng song song với trục tọa độ, với phương trình y = ax² + bx + c hoặc x = ay² + by + c.

Khi parabol có trục đối xứng không song song với các trục tọa độ, phương trình của nó sẽ phức tạp hơn và thường được viết dưới dạng tổng quát Ax² + Bxy + Cy² + Dx + Ey + F = 0. Việc chuyển từ dạng tổng quát sang dạng chuẩn tắc thường đòi hỏi phép biến đổi tọa độ phù hợp.

Phương pháp giải bài tập về parabol

Để giải các bài tập về parabol, cần xác định rõ các yếu tố đặc trưng như đỉnh, trục đối xứng và hướng mở của parabol. Phương pháp giải thường bắt đầu bằng việc đưa phương trình về dạng chuẩn tắc thông qua các phép biến đổi đại số.

Trong nhiều trường hợp, việc vẽ đồ thị parabol sẽ giúp hình dung rõ hơn về bài toán. Các tính chất đối xứng và khoảng cách từ điểm đến tiêu điểm cũng là công cụ quan trọng để giải quyết các bài toán phức tạp về parabol.

Mối liên hệ với các đường conic khác

Parabol là một trường hợp đặc biệt của đường conic, có mối liên hệ mật thiết với ellip và hyperbola. Khi độ lệch tâm của một đường conic bằng 1, ta được một parabol. Điều này giải thích tại sao parabol có thể được xem như một ellip với một tiêu điểm ở vô cực.

Trong thực tế, sự chuyển đổi giữa các đường conic thường được ứng dụng trong thiết kế quang học và kiến trúc. Ví dụ, khi cắt một mặt nón tròn xoay bởi một mặt phẳng song song với một đường sinh của nón, mặt cắt thu được chính là một parabol.

Kiến thức về phương trình parabol trong chương trình lớp 10

Phương trình parabol lớp 10 là một dạng phương trình bậc hai có dạng y = ax² + bx + c (với a ≠ 0), biểu diễn một đường cong trên mặt phẳng tọa độ. Đây là kiến thức quan trọng giúp học sinh hiểu về mối quan hệ giữa đại số và hình học, đồng thời ứng dụng trong nhiều bài toán thực tế.

Để nắm vững kiến thức này, học sinh cần hiểu rõ các thành phần cơ bản và phương pháp giải các dạng bài tập thường gặp. Việc thực hành qua các ví dụ minh họa sẽ giúp củng cố kiến thức và phát triển kỹ năng giải toán.

Nội dung cơ bản cần nắm vững

Công thức tính parabol bao gồm các yếu tố quan trọng như hệ số a, b, c và các đặc trưng của đường cong. Hệ số a quyết định chiều mở của parabol, khi a > 0 parabol mở lên trên và khi a < 0 parabol mở xuống dưới.

Đỉnh của parabol có tọa độ (-b/2a, -Δ/4a) với Δ = b² – 4ac là điểm quan trọng xác định vị trí cao nhất hoặc thấp nhất của đường cong. Trục đối xứng của parabol có phương trình x = -b/2a.

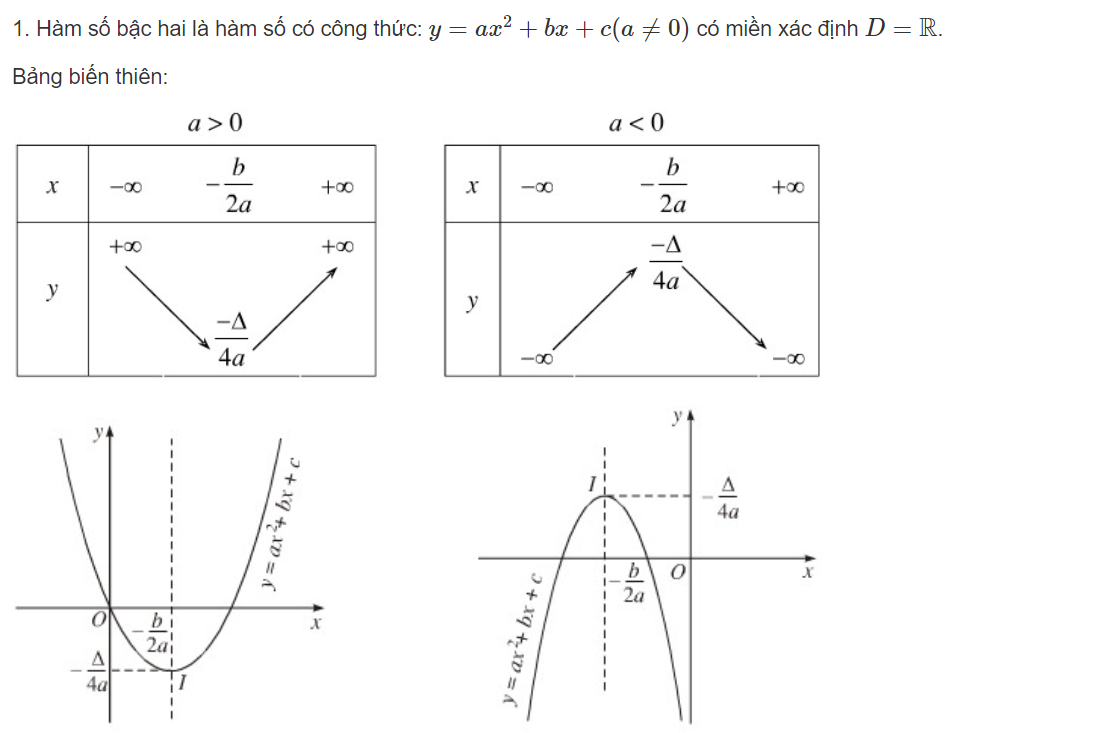
Giao điểm của parabol với trục Ox được xác định bằng cách giải phương trình ax² + bx + c = 0. Số nghiệm của phương trình phụ thuộc vào giá trị của Δ.

Phương pháp giải các dạng bài tập điển hình

Phương trình đường parabol thường xuất hiện trong các dạng bài tập như: xác định tọa độ đỉnh, tìm trục đối xứng, tìm giao điểm với trục tọa độ và vẽ đồ thị.

Khi giải bài tập về parabol, cần tuân theo các bước cơ bản:

• Xác định các hệ số a, b, c từ phương trình đã cho
• Tính định thức Δ = b² – 4ac
• Xác định tọa độ đỉnh và trục đối xứng
• Tìm giao điểm với trục tọa độ nếu cần
• Vẽ đồ thị dựa trên các yếu tố đã tìm được

Một số bài tập minh họa và hướng dẫn giải

Ví dụ 1: Cho phương trình y = x² – 2x – 3

• Bước 1: Xác định a = 1, b = -2, c = -3
• Bước 2: Tính Δ = (-2)² – 4(1)(-3) = 16
• Bước 3: Tọa độ đỉnh (1, -4)
• Bước 4: Giao điểm với Ox tại x = -1 và x = 3

Ví dụ 2: Cho phương trình y = -2x² + 4x + 1

• Bước 1: Xác định a = -2, b = 4, c = 1
• Bước 2: Tính Δ = 4² – 4(-2)(1) = 24
• Bước 3: Tọa độ đỉnh (1, 3)
• Bước 4: Giao điểm với Ox tại x ≈ -0.45 và x ≈ 2.45

Việc thực hành giải nhiều bài tập với độ khó tăng dần sẽ giúp học sinh nắm vững kiến thức và phát triển kỹ năng giải toán hiệu quả.

Phương trình parabol là một trong những khái niệm quan trọng trong toán học, cung cấp nền tảng cho nhiều kiến thức liên quan đến hình học và đại số. Việc hiểu rõ về phương trình parabol giúp học sinh có thể ứng dụng hiệu quả trong các bài tập, đồng thời phát triển tư duy giải toán một cách logic. Qua bài viết, các đặc điểm, dạng phương trình và cách viết cụ thể đã được đề cập, giúp người học dễ dàng tiếp cận và áp dụng trong thực tế học tập.