Cộng/trừ 2 ma trận là một trong những nội dung cơ bản nhất trong bộ môn toán cao cấp. Đây là dạng kiến thức phức tạp, dễ gây nhầm lẫn với không ít sinh viên. Bài viết dưới đây, chúng tôi sẽ cung cấp đầy đủ cho các bạn cách thực hiện cộng/trừ 2 ma trận và ví dụ minh họa.
Ma trận là gì?
Ma trận (matrix) là một tập hợp các phần tử được sắp xếp thành một dạng bảng gồm nhiều hàng và nhiều cột. Mỗi phần tử trong ma trận được xác định bởi vị trí của nó trong bảng, được biểu diễn bằng chỉ số hàng và chỉ số cột.

Một ma trận thường được ký hiệu bằng một ký tự in đậm, chẳng hạn như A, B, C, … và các phần tử của ma trận được biểu diễn bằng cùng ký tự nhưng có chỉ số hàng và cột đi kèm, ví dụ: aij là phần tử ở hàng thứ i và cột thứ j của ma trận A.
Ví dụ, ma trận A có kích thước 3×4 (3 hàng và 4 cột) có thể được biểu diễn như sau:
A = [ a11 a12 a13 a14 ]
[ a21 a22 a23 a24 ]
[ a31 a32 a33 a34 ]
Ma trận là một khái niệm quan trọng trong đại số tuyến tính và được sử dụng rộng rãi trong nhiều lĩnh vực của toán học, vật lý, kỹ thuật, khoa học máy tính và nhiều lĩnh vực khác. Chúng cho phép biểu diễn và thao tác trên các tập hợp số liệu một cách hiệu quả và mạnh mẽ.
Tính chất của phép cộng/trừ hai ma trận
Phép cộng và trừ ma trận có một số tính chất quan trọng như sau:
Tính giao hoán
Trong phép cộng ma trận, tính chất giao hoán được thỏa mãn, tức là: A + B = B + A. Tuy nhiên, trong phép trừ ma trận, tính chất giao hoán không được thỏa mãn, vì: A – B ≠ B – A
Tính kết hợp
Cả phép cộng và trừ ma trận đều thỏa mãn tính kết hợp, có nghĩa là: (A + B) + C = A + (B + C), (A – B) – C = A – (B – C) = A – B + C
Tính phân phối
Phép nhân một ma trận với một số vô hướng có thể được phân phối qua phép cộng hoặc trừ, tức là: k(A + B) = kA + kB, k(A – B) = kA – kB
Phần tử đơn vị
Trong phép cộng ma trận, ma trận không (ma trận có tất cả các phần tử bằng 0) đóng vai trò là phần tử đơn vị, tức là: A + 0 = 0 + A = A. Tuy nhiên, trong phép trừ ma trận, không có phần tử đơn vị tương ứng.
Phần tử nghịch đảo
Đối với phép cộng ma trận, mỗi ma trận A có phần tử nghịch đảo là -A, sao cho: A + (-A) = 0. Tuy nhiên, trong phép trừ ma trận, không có khái niệm phần tử nghịch đảo tương tự.
Những tính chất này giúp ta hiểu sâu hơn về cách thức hoạt động của phép trừ và cộng hai ma trận, cũng như mối liên hệ của chúng với các phép toán khác trong đại số tuyến tính.
Hướng dẫn cộng/trừ 2 ma trận
Để thực hiện cộng/trừ 2 ma trận, bạn cần thực hiện đầy đủ các bước sau:
Xác định kích thước 2 ma trận
Cộng trừ 2 ma trận là một phép toán cơ bản và quan trọng trong đại số tuyến tính. Để thực hiện được phép cộng hoặc trừ hai ma trận, điều kiện tiên quyết là hai ma trận đó phải có cùng kích thước, tức là cùng số hàng và số cột. Nếu không thỏa mãn điều kiện này, thì phép cộng trừ sẽ không thể thực hiện được.
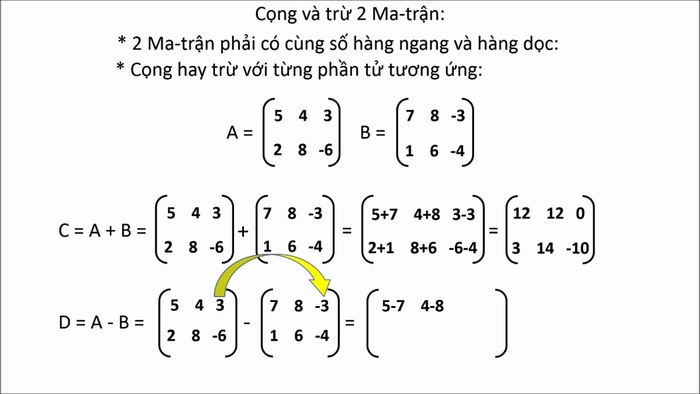
Thực hiện tính toán trên từng phần tử
Khi hai ma trận đã có cùng kích thước, chúng ta có thể tiến hành cộng hoặc trừ hai ma trận bằng cách thực hiện phép toán tương ứng trên từng phần tử của hai ma trận. Cụ thể, để cộng hai ma trận, ta cộng từng phần tử tương ứng của chúng lại với nhau. Để thực hiện phép trừ hai ma trận, ta đảo dấu của ma trận thứ hai rồi cộng nó với ma trận thứ nhất.
Ghi kết quả từng phần tử vào ma trận kết quả
Trong quá trình cộng hoặc trừ, chúng ta di chuyển từ trái sang phải, từ trên xuống dưới, thực hiện phép toán trên từng phần tử tương ứng của hai ma trận. Kết quả của phép trừ hoặc cộng 2 ma trận sẽ là một ma trận mới có cùng kích thước với hai ma trận ban đầu, trong đó mỗi phần tử là tổng hoặc hiệu của hai phần tử tương ứng trong hai ma trận gốc.
Phép cộng trừ hai ma trận là nền tảng cho nhiều phép toán khác trong đại số tuyến tính, như nhân ma trận, tính định thức, tìm ma trận nghịch đảo, và giải hệ phương trình tuyến tính. Nó giúp đơn giản hóa các phép toán phức tạp hơn và có ứng dụng rộng rãi trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật, khoa học máy tính, và nhiều lĩnh vực khác nữa.
Ví dụ minh họa cộng/trừ hai ma trận
Để bạn nắm rõ hơn về cách thực hiện phép cộng và trừ với 2 ma trận, chúng tôi có ví dụ như sau:
Ví dụ cộng 2 ma trận
Ta có 2 ma trận A và B như sau: A=|3;5] và B=[4;7] với A+B = C[c1;c2]
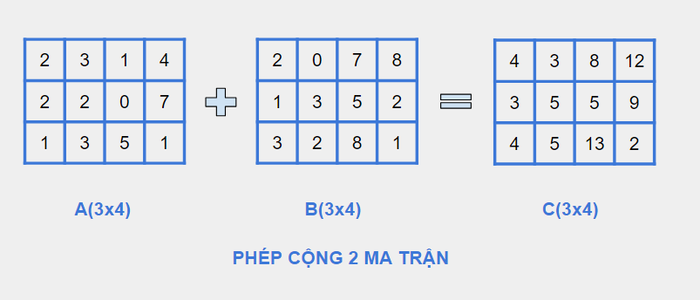
- Bước 1: Xác định kích thước 2 ma trận: Ma trận A kích thước 1×2, ma trận B kích thước 1×2.
- Bước 2: Xác định phần tử: a1=3, a2=5, b1=4, b2=7.
- Bước 3: Tính kết quả của ma trận phần từ: a1+b1=c1 => c1=7, a2+b2=c2 => c2=12. Vậy ma trận C=[7:12]
Ví dụ trừ 2 ma trận
Ta có 2 ma trận A và B như sau: A=|4;6] và B=[3;1] với A+B = C[c1;c2]
- Bước 1: Xác định kích thước 2 ma trận: Ma trận A kích thước 1×2, ma trận B kích thước 1×2.
- Bước 2: Xác định phần tử: a1=4, a2=6, b1=3, b2=1.
- Bước 3: Tính kết quả của ma trận phần từ: a1-b1=c1 => c1=1, a2-b2=c2 => c2=5. Vậy ma trận C=[1:5]
Lời kết
Phép cộng/trừ ma trận là hai phép toán cơ bản và quan trọng trong đại số tuyến tính. Việc hiểu rõ khái niệm, tính chất và ứng dụng của phép cộng và trừ ma trận sẽ giúp ích cho học sinh, sinh viên và những người làm việc trong các lĩnh vực liên quan đến toán học và khoa học máy tính.




