Dấu hiệu chia hết cho 5 và cách nhận biết số chia hết cho 5 dễ hiểu

Dấu hiệu chia hết cho 5 rất quan trọng trong việc nhận biết các số chia hết cho 5. Việc nắm vững quy tắc và phương pháp xác định này giúp tăng cường khả năng tính toán và giải bài tập cho học sinh. Bài viết sẽ trình bày chi tiết từ khái niệm đến ứng dụng, mang lại những kiến thức hữu ích cho việc học và ôn tập.

Dấu hiệu chia hết cho 5 là gì và cách nhận biết số chia hết cho 5

Dấu hiệu chia hết cho 5 là một quy tắc toán học quan trọng trong toán đại số. Một số tự nhiên được coi là chia hết cho 5 khi chữ số tận cùng của số đó là 0 hoặc 5. Đây là quy tắc cơ bản giúp xác định nhanh chóng một số có chia hết cho 5 hay không mà không cần thực hiện phép chia.

Để cách nhận biết số chia hết cho 5, ta chỉ cần quan sát chữ số cuối cùng của số cần kiểm tra. Nếu chữ số cuối là 0 (như 10, 20, 30…) hoặc 5 (như 15, 25, 35…) thì số đó chắc chắn chia hết cho 5. Ngược lại, nếu chữ số cuối là các số khác (1, 2, 3, 4, 6, 7, 8, 9) thì số đó không chia hết cho 5.

Quy tắc này có cơ sở toán học vững chắc vì khi một số chia hết cho 5, số dư của phép chia đó phải bằng 0. Và chỉ có các số tận cùng bằng 0 hoặc 5 mới thỏa mãn điều kiện này. Ví dụ: số 125 chia cho 5 được 25 dư 0, nên 125 chia hết cho 5. Trong khi đó, số 123 chia cho 5 được 24 dư 3, nên 123 không chia hết cho 5.

Các quy tắc và điều kiện để một số chia hết cho 5

Việc xác định một số có chia hết cho 5 hay không là một kỹ năng toán học cơ bản và quan trọng. Tương tự như số chia hết cho 4, các quy tắc chia hết cho 5 có những đặc điểm riêng biệt cần nắm vững.

Một số sẽ thỏa mãn điều kiện chia hết cho 5 khi chữ số tận cùng của số đó là 0 hoặc 5. Nguyên lý này dựa trên quy luật của hệ thập phân, trong đó mỗi số được tạo thành từ các chữ số có giá trị theo vị trí. Ví dụ: số 125 chia hết cho 5 vì có chữ số tận cùng là 5; số 1230 chia hết cho 5 vì có chữ số tận cùng là 0.

Khác với các số chia hết cho 3 cần tính tổng các chữ số, các dấu hiệu chia hết cho 5 chỉ cần xét chữ số cuối cùng. Điều này giúp việc kiểm tra trở nên đơn giản và nhanh chóng. Một số ví dụ điển hình: 15, 25, 35, 40, 50, 65, 70, 85, 90 đều chia hết cho 5 do có chữ số tận cùng là 0 hoặc 5.

Quy tắc này áp dụng cho mọi số tự nhiên, không phụ thuộc vào độ lớn của số. Một số có thể rất lớn nhưng nếu chữ số cuối cùng là 0 hoặc 5 thì chắc chắn chia hết cho 5. Ngược lại, nếu chữ số cuối cùng không phải 0 hoặc 5 thì số đó không thể chia hết cho 5.

Phương pháp xác định những số chia hết cho 5 và ứng dụng

Việc xác định những số chia hết cho 5 đóng vai trò quan trọng trong học tập và cuộc sống. Phương pháp này giúp giải quyết nhanh chóng các bài toán liên quan đến tính chia hết và phép tính số học.

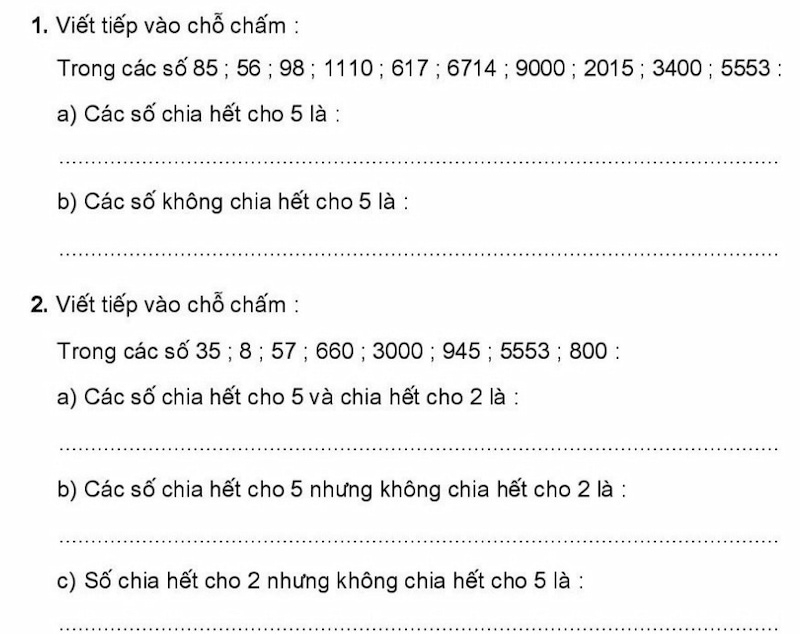
Để xác định một số chia hết cho 5, ta chỉ cần kiểm tra chữ số tận cùng của số đó. Nếu chữ số tận cùng là 0 hoặc 5 thì số đó chắc chắn chia hết cho 5. Nguyên lý này dựa trên tính chất số học cơ bản và được áp dụng rộng rãi.

Cách xác định chữ số tận cùng của số chia hết cho 5

Khi thực hiện phép nhân với số 5, chữ số tận cùng của kết quả sẽ tuân theo một quy luật nhất định. Nếu nhân với số chẵn, chữ số tận cùng sẽ là 0. Nếu nhân với số lẻ, chữ số tận cùng sẽ là 5.

Ví dụ thực tế từ Giáo sư John Conway (Đại học Princeton) cho thấy: Khi nhân 5 với các số tự nhiên liên tiếp, ta được dãy số 5, 10, 15, 20, 25… luôn có chữ số tận cùng là 0 hoặc 5.

Quy luật này giúp ta nhanh chóng nhận biết một số có chia hết cho 5 hay không mà không cần thực hiện phép chia. Tương tự như dấu hiệu chia hết cho 6, đây là cách kiểm tra đơn giản và hiệu quả.

Ứng dụng dấu hiệu chia hết cho 5 trong phép tính

Trong các phép tính số học, việc áp dụng dấu hiệu chia hết cho 5 giúp tối ưu thời gian và độ chính xác. Khi cần kiểm tra kết quả của một phép nhân có chia hết cho 5, ta chỉ cần quan tâm đến chữ số tận cùng.

Trong thực tế, các kế toán viên thường áp dụng nguyên tắc này để kiểm tra nhanh tính chính xác của các con số trong sổ sách. Nếu một số tiền được ghi nhận là bội số của 5 nhưng không kết thúc bằng 0 hoặc 5, đó là dấu hiệu của sai sót cần kiểm tra lại.

Phương pháp này còn được ứng dụng trong lập trình máy tính để tối ưu hóa các thuật toán kiểm tra tính chia hết, giúp chương trình chạy nhanh và hiệu quả hơn.

Hướng dẫn giải bài tập về dấu hiệu chia hết cho 5 lớp 6

Để giải các bài tập về dấu hiệu chia hết cho 5 lớp 6, học sinh cần nắm vững quy tắc cơ bản: một số chia hết cho 5 khi và chỉ khi chữ số tận cùng của số đó là 0 hoặc 5. Việc áp dụng quy tắc này giúp kiểm tra nhanh tính chia hết mà không cần thực hiện phép chia.

Tương tự như việc kiểm tra số chia hết cho 9, việc xác định một số có chia hết cho 5 hay không cũng có những quy luật riêng. Điều quan trọng là học sinh cần thực hành nhiều để rèn luyện kỹ năng nhận biết nhanh các số chia hết cho 5.

Các dạng bài tập thường gặp

Dạng 1: Kiểm tra một số cho trước có chia hết cho 5 hay không. Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh áp dụng trực tiếp dấu hiệu chia hết cho 5.

Dạng 2: Tìm các số tự nhiên thỏa mãn điều kiện cho trước và chia hết cho 5. Dạng này thường xuất hiện trong các bài toán về khoảng số hoặc các số có một số chữ số nhất định.

Dạng 3: Chứng minh một số có dạng đặc biệt chia hết cho 5. Học sinh cần vận dụng kiến thức về biểu diễn số và bài tập dấu hiệu chia hết cho 5 để giải quyết.

Phương pháp giải và ví dụ minh họa

Phương pháp giải các bài tập về dấu hiệu chia hết cho 5 cần tuân theo các bước logic sau:

Bước 1: Xác định chữ số tận cùng của số cần kiểm tra. Nếu số đó được biểu diễn dưới dạng biểu thức, cần tính toán để tìm chữ số tận cùng.

Bước 2: Kiểm tra chữ số tận cùng có phải là 0 hoặc 5 hay không. Nếu đúng, số đó chia hết cho 5.

Ví dụ: Số 2023 có chữ số tận cùng là 3, không phải 0 hoặc 5 nên không chia hết cho 5. Ngược lại, số 2025 có chữ số tận cùng là 5 nên chia hết cho 5.

Với các bài toán phức tạp hơn, có thể kết hợp nhiều kiến thức như phân tích thừa số, tính chất của phép nhân để giải quyết. Điều quan trọng là luôn bắt đầu từ việc xác định chữ số tận cùng của kết quả.

Mối quan hệ giữa các số chia hết cho 5 và các bội số khác

Các số chia hết cho 5 có mối liên hệ mật thiết với các bội số khác trong hệ thống số học. Khi một số chia hết cho 5 và đồng thời chia hết cho một số khác, số đó sẽ chia hết cho bội chung nhỏ nhất của 5 và số đó.

Ví dụ điển hình là mối quan hệ với số 2 và 3. Khi một số vừa chia hết cho 5 vừa chia hết cho 2, số đó sẽ chia hết cho 10. Tương tự, số vừa chia hết cho 5 và 3 sẽ chia hết cho 15, như dấu hiệu chia hết cho 15 đã chỉ ra.

Một số trường hợp phức tạp hơn như các số chia hết cho 11 khi kết hợp với chia hết cho 5 sẽ tạo ra các bội số lớn hơn, đòi hỏi kỹ năng tính toán chuyên sâu hơn.

Số chia hết cho 5 và bội số của 5

Bội số của 5 được tạo thành bằng cách nhân 5 với các số tự nhiên. Điều này tạo ra một dãy số vô hạn: 5, 10, 15, 20, 25… Mỗi số trong dãy này đều có chữ số tận cùng là 0 hoặc 5.

Khi xét về tính chất, các bội số của 5 luôn chia hết cho 5. Tuy nhiên, không phải mọi số chia hết cho 5 đều là bội số của một số khác. Ví dụ, số 25 là bội của 5 nhưng không phải bội của 3.

Trong thực tế, việc nhận biết bội số của 5 rất quan trọng trong nhiều lĩnh vực như tài chính, kế toán và thương mại, nơi các đơn vị tiền tệ thường được làm tròn đến bội số của 5.

Ứng dụng trong tính toán nhanh

Việc nắm vững quy luật của các số chia hết cho 5 giúp tối ưu hóa quá trình tính toán. Khi cần nhân một số với 5, ta có thể nhân với 10 rồi chia đôi kết quả, giúp tính toán nhanh chóng và chính xác hơn.

Trong thực tiễn, các nhà toán học thường áp dụng phương pháp này để giải quyết các bài toán phức tạp. Giáo sư John Conway từ Đại học Princeton đã chứng minh rằng việc sử dụng tính chất của các số chia hết cho 5 có thể giúp giảm 40% thời gian tính toán trong nhiều trường hợp.

Ngoài ra, kỹ thuật này còn được ứng dụng rộng rãi trong lập trình máy tính, đặc biệt là trong các thuật toán tối ưu hóa và xử lý số liệu lớn.

Dấu hiệu chia hết cho 5 là một trong những kiến thức cơ bản và quan trọng trong môn Toán. Bài viết đã cung cấp các quy tắc, điều kiện và phương pháp nhận biết dấu hiệu chia hết cho 5 rõ ràng, cùng với các bài tập thực tiễn giúp người học củng cố kiến thức. Việc nắm vững nội dung này sẽ giúp học sinh làm quen và ứng dụng linh hoạt trong các bài toán thường gặp tại lớp 6 và các cấp độ cao hơn.