Hình hộp tam giác là gì? Đây là một loại đa diện đặc biệt, nó còn được gọi là lăng trụ tam giác. Bài viết này sẽ đi sâu vào tìm hiểu về định nghĩa hình hộp tam giác là gì, đặc điểm, tính chất và các yếu tố quan trọng liên quan đến hình hộp tam giác trong hình học không gian.
Hình hộp tam giác là gì?
Hình hộp tam giác (lăng trụ tam giác) là một hình khối được tạo thành từ hai đa giác bằng nhau và song song với nhau, được gọi là hai đáy. Các mặt bên của hình hộp tam giác là các hình bình hành. Với nhiều đặc tính đặc biệt, hình hộp tam giác đã trở thành một khái niệm quan trọng trong toán học và ứng dụng của nó cũng rất đa dạng.
Các loại lăng trụ tam giác phổ biến
Có nhiều cách phân loại hình hộp tam giác dựa trên các đặc điểm khác nhau. Dưới đây là một số loại phổ biến:
Phân loại theo dạng hai đáy
- Hình hộp tam giác đều: Hai đáy là hai tam giác đều.
- Hình hộp tam giác cân: Hai đáy là hai tam giác cân.
- Hình hộp tam giác vuông: Hai đáy là hai tam giác vuông.
Phân loại theo hình dạng mặt bên
- Hình hộp tam giác đều: Tất cả các mặt bên đều là hình bình hành đều.
- Hình hộp tam giác vuông: Một số mặt bên là hình chữ nhật.
- Hình hộp tam giác cân: Một số mặt bên là hình thang cân.
Với các dạng khác nhau, hình hộp tam giác có thể được sử dụng trong nhiều bài toán và ứng dụng khác nhau.
Cách tính diện tích và chu vi lăng trụ tam giác
Các công thức tính diện tích của khối hộp tam giác bao gồm diện tích các mặt đáy, diện tích mặt bên và diện tích toán phần.
Diện tích mặt đáy
Diện tích mặt đáy của lăng trụ tam giác bằng diện tích của một tam giác bất kỳ, tùy thuộc vào dạng tam giác đáy (vuông, cân, đều, nhọn,…).
Công thức chung:
- Diện tích tam giác vuông:
(với a, b là hai cạnh vuông góc)
- Diện tích tam giác cân:
(với b là cạnh đáy, h là chiều cao hạ từ đỉnh xuống cạnh đáy)
- Diện tích tam giác đều:
(với a là cạnh của tam giác đều)
- Diện tích tam giác nhọn:
(với b là cạnh đáy, h là chiều cao hạ từ đỉnh xuống cạnh đáy)
Lưu ý:
- Cần xác định dạng tam giác đáy trước khi áp dụng công thức tính diện tích phù hợp.
- Các ký hiệu trong công thức cần được thay thế bằng giá trị thực tế của các cạnh hoặc chiều cao.
Diện tích các mặt bên hình hộp tam giác
Diện tích mỗi mặt bên của lăng trụ tam giác bằng diện tích của một hình chữ nhật có chiều dài bằng cạnh đáy tam giác và chiều rộng bằng chiều cao của lăng trụ.
Công thức:
Trong đó:
- Smb là diện tích một mặt bên
- a là cạnh đáy tam giác
- h là chiều cao của lăng trụ
Diện tích toàn phần
Diện tích toàn phần của lăng trụ tam giác bằng tổng diện tích tất cả các mặt, bao gồm:
- Diện tích hai mặt đáy
- Diện tích các mặt bên
Công thức:
Trong đó:
- Stp là diện tích toàn phần
- Sd là diện tích một mặt đáy
- n là số lượng mặt bên
- Smb là diện tích một mặt bên
Lưu ý:
- Số lượng mặt bên (n) bằng số cạnh đáy của lăng trụ tam giác.
Ví dụ về tính diện tích hình hộp tam giác
Để hiểu rõ hơn về cách tính diện tích khối hộp tam giác, chúng ta cùng xem một ví dụ cụ thể.
Một công ty lấy hình hộp tam giác làm đơn vị đóng gói cho sản phẩm mới của mình. Kích thước của hộp là 10cm x 15cm x 20cm. Hãy tính diện tích tổng thể của hình hộp này.
Bước 1: Tính diện tích đáy
Vì hình hộp tam giác được hình thành từ một hình tam giác, diện tích đáy sẽ bằng diện tích tam giác ban đầu. Ta có:
Bước 2: Tính diện tích mặt bên
Để tính diện tích mặt bên, ta cần biết chu vi của tam giác đáy. Vì đây là hình tam giác vuông, ta có thể sử dụng định lý Pythagoras để tính được chu vi:
Với a và b lần lượt là hai cạnh góc vuông của tam giác đáy, c là độ dài cạnh còn lại.
Ta có:
Suy ra:
Chu vi của tam giác đáy là
Diện tích mặt bên sẽ bằng:
Bước 3: Tính diện tích tổng thể
Tổng diện tích của hình hộp tam giác sẽ bao gồm diện tích đáy và diện tích các mặt bên, ta có:
Vậy diện tích tổng thể của hình hộp tam giác này là khoảng 2,580cm^2.
Chu vi
Chu vi của hình hộp tam giác là tổng độ dài của tất cả các cạnh của hình hộp. Đơn giản hơn, đó chính là khoảng cách quanh hình hộp tam giác. Để tính chu vi của hình hộp tam giác, chúng ta cần biết độ dài của các cạnh của nó.
Ký hiệu
Trong công thức tính chu vi hình hộp tam giác, chúng ta sẽ sử dụng các ký hiệu sau:
- Chu vi: P
- Độ dài cạnh đáy: a, b, c
- Độ dài cạnh bên: h
Công thức tổng quát
Công thức tính chu vi hình hộp tam giác có dạng:
Các loại chu vi lăng trụ tam giác
Lăng trụ tam giác có thể được phân loại dựa trên hình dạng của đáy và cạnh bên. Dưới đây là những dạng chu vi phổ biến của lăng trụ tam giác.
Lăng trụ tam giác đều
Đây là một trong những dạng chu vi đơn giản nhất của lăng trụ tam giác. Đặc điểm của lăng trụ tam giác đều là:
- Đáy là tam giác đều.
- Cạnh bên vuông góc với đáy.
- Chu vi:
(a là độ dài cạnh đáy, h là độ dài cạnh bên)
Lăng trụ tam giác vuông
Đây là một dạng chu vi phổ biến khác của lăng trụ tam giác. Thay vì có đáy là tam giác đều, lăng trụ tam giác vuông có đáy là tam giác vuông. Điều này ảnh hưởng đến công thức tính chu vi như sau:
- Đáy là tam giác vuông.
- Cạnh bên vuông góc với đáy.
- Chu vi:
(a, b, c là độ dài các cạnh đáy, h là độ dài cạnh bên)
Lăng trụ tam giác tù
Trong trường hợp đáy của lăng trụ tam giác là tam giác tù, công thức tính chu vi sẽ có sự khác biệt nhất định. Chúng ta sẽ cần tính toán độ dài của từng cạnh riêng lẻ và cộng lại để có được chu vi cuối cùng.
Ứng dụng của hình hộp tam giác trong thực tế
Hình hộp tam giác có mặt bên là các hình bình hành, tương tự như các khối hình khác như hình lập phương hay hình chóp. Với tính chất đặc biệt này, hình hộp tam giác được sử dụng rộng rãi trong ngành xây dựng và kiến trúc. Chẳng hạn, nó có thể được sử dụng để tạo nên các cấu trúc như nhà khi có nhiều tầng hoặc cầu vượt.
Ngoài ra, hình hộp tam giác cũng có thể được áp dụng trong việc tính toán diện tích và thể tích của các vật thể trong đời sống hàng ngày. Chẳng hạn, khi bạn muốn mua một chiếc hộp để đựng đồ, việc tính toán diện tích và thể tích của nó sẽ giúp bạn chọn được sản phẩm phù hợp với nhu cầu của mình.
Phân biệt hình hộp tam giác với các hình khối khác
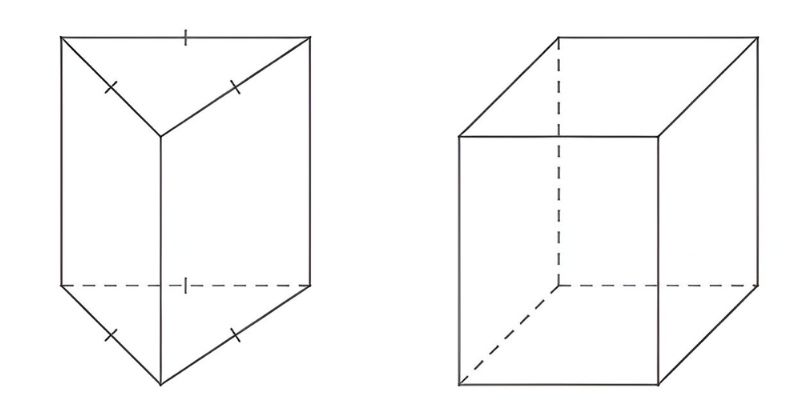 Trong toán học, có nhiều loại hình khối khác nhau và nhiều khi chúng ta có thể nhầm lẫn giữa chúng. Vì vậy, để phân biệt hình hộp tam giác với các hình khối khác, chúng ta cần hiểu rõ tính chất và đặc điểm của nó.
Trong toán học, có nhiều loại hình khối khác nhau và nhiều khi chúng ta có thể nhầm lẫn giữa chúng. Vì vậy, để phân biệt hình hộp tam giác với các hình khối khác, chúng ta cần hiểu rõ tính chất và đặc điểm của nó.
Theo dõi bảng dưới đây để biết sự khác biệt giữa hình hộp tam giác và các dạng hình lăng trụ khác.
| Đặc điểm | Lăng trụ tam giác (hình hộp tam giác) | Lăng trụ tứ giác | Lăng trụ ngũ giác | Lăng trụ n giác (n > 5) |
| Mặt đáy | 2 tam giác bằng nhau, song song với nhau | 2 tứ giác (có thể là hình vuông, hình chữ nhật, hình bình hành) bằng nhau, song song với nhau | 2 ngũ giác bằng nhau, song song với nhau | 2 đa giác n cạnh (có thể là hình n cạnh đều, hình thang cân,…) bằng nhau, song song với nhau |
| Mặt bên | Hình chữ nhật | Hình chữ nhật | Hình chữ nhật | Hình chữ nhật |
| Số cạnh | 12 | 14 | 16 | 2n |
| Số đỉnh | 8 | 10 | 12 | n + 2 |
| Góc | 4 góc nhọn, 4 góc tù | 8 góc nhọn | 10 góc nhọn | 2n góc nhọn |
| Cạnh bên | Vuông góc với mặt đáy | Vuông góc với mặt đáy | Vuông góc với mặt đáy | Vuông góc với mặt đáy |
| Ví dụ | Hộp bút chì, hộp sữa | Hộp giày, tủ sách | Lăng kính ngũ giác | Lều trại |
Các bài toán liên quan đến hình hộp tam giác
Trong toán học, hình hộp tam giác cũng thường được sử dụng trong các bài toán liên quan đến hình học và không gian. Dưới đây là một số bài toán phổ biến liên quan đến hình hộp tam giác:
Bài toán tính diện tích và thể tích của hình hộp tam giác
- Cho biết chiều cao và độ dài cạnh đáy, tính diện tích và thể tích của hình hộp tam giác.
- Cho biết thể tích và chiều cao, tính độ dài cạnh đáy của hình hộp tam giác.
Bài toán tính cạnh và độ dài đường chéo của một mặt bên
- Cho biết diện tích và chiều cao của một mặt bên, tính cạnh và độ dài đường chéo của nó.
- Cho biết cạnh và độ dài đường chéo của một mặt bên, tính diện tích và chiều cao của nó.
Kết luận
Như vậy, hình hộp tam giác là một khái niệm quan trọng trong toán học và có rất nhiều ứng dụng trong thực tế. Nó có tính chất đặc trưng và có thể được phân loại theo nhiều tiêu chí khác nhau. Để giải quyết các bài toán liên quan đến nó, các em học sinh cần nắm vững các đặc điểm cũng như những nội dung, công thức của nó.
Nội dung bài viết
- 1. Hình hộp tam giác là gì?
- 2. Các loại lăng trụ tam giác phổ biến
- 3. Cách tính diện tích và chu vi lăng trụ tam giác
- 4. Ví dụ về tính diện tích hình hộp tam giác
- 5. Các loại chu vi lăng trụ tam giác
- 6. Ứng dụng của hình hộp tam giác trong thực tế
- 7. Phân biệt hình hộp tam giác với các hình khối khác
- 8. Các bài toán liên quan đến hình hộp tam giác
- 9. Kết luận