Diện tích hình thang là một trong những khái niệm cơ bản trong hình học không gian. Nó được tính dựa trên chiều cao và tổng độ dài hai đáy của hình. Đây là một thuật toán đơn giản nhưng lại có nhiều ứng dụng thực tiễn trong các bài toán về diện tích đất đai, xây dựng và nhiều lĩnh vực khác. Để hiểu rõ hơn, mời các bạn cùng theo dõi thông tin chi tiết trong bài viết dưới đây.
Công thức tính diện tích hình thang là gì?
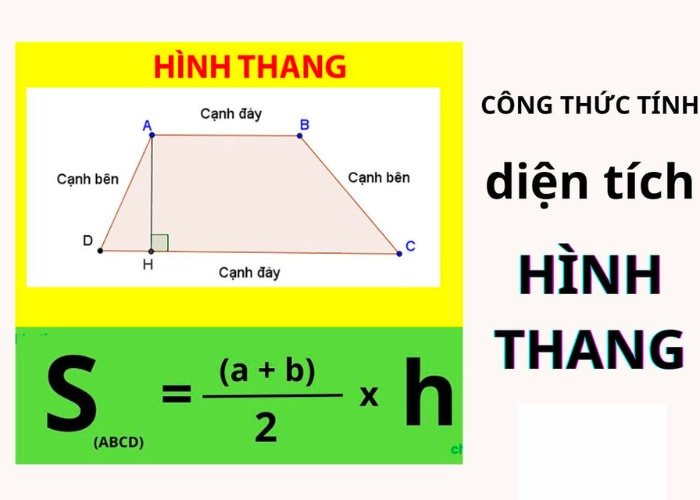
Cách tính diện tích hình thang: Cộng chiều dài hai cạnh đáy, nhân với chiều cao, rồi chia cho 2.
Công thức chung
DT hình thang được tính theo công thức sau:
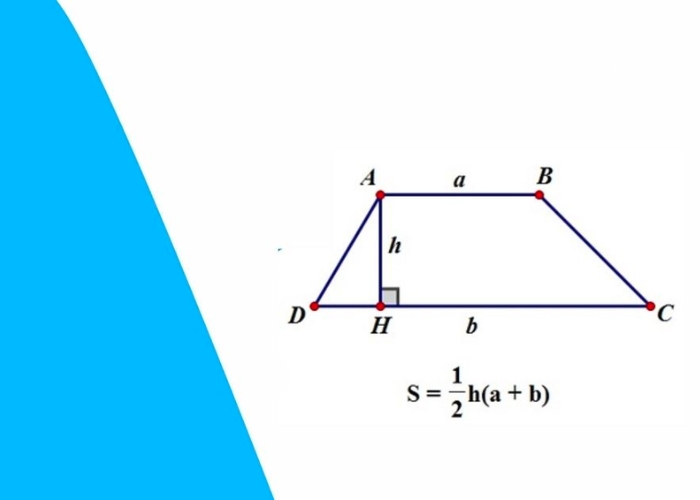
$$S=h\times\frac{\left(a+b\right)}2$$
Trong đó:
- S là diện tích hình thang.
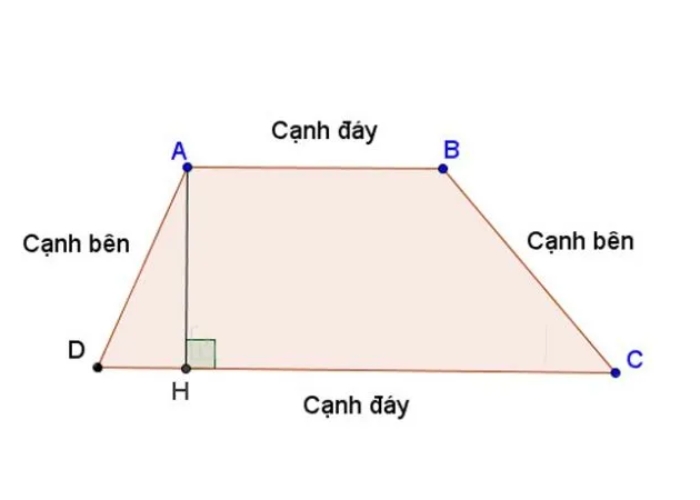
- h là chiều cao, đường từ đỉnh đến đáy và vuông góc với đáy.
- a, b là chiều dài của hai cạnh đáy.
Đọc ngay: Hình thang là gì? Khái niệm, tính chất và đặc điểm cơ bản
Công thức tính hình thang cân
Khi tính diện tích hình thang cân, chúng ta cũng có thể sử dụng công thức chung đã được giới thiệu ở mục trên. Hình thang cân có hai cạnh đáy và hai góc kề của một đáy bằng nhau. Do đó khi áp dụng công thức, bạn nên chia hình thang thành các phần nhỏ hơn để tính rồi cộng lại.
Công thức tính hình thang vuông
Hình thang vuông có đặc điểm là chứa 2 góc 90 độ và một trong hai cạnh bên vuông góc với cả hai đáy. Để tính diện tích của hình thang vuông, bạn sử dụng công thức:
$$S=h\times\frac{\left(a+b\right)}2$$
Trong đó:
- S là diện tích hình thang.
- h là chiều cao (cạnh bên vuông góc với hai đáy)
- a và b là chiều dài của hai cạnh đáy.
Xem ngay: Cách tính chu vi hình thang? Công thức, bài tập mẫu vận dụng
Ví dụ cách tính diện dt hình thang
Ví dụ dưới đây sẽ giúp bạn hiểu rõ hơn về cách áp dụng công thức tính dt hình thang ở mục trên.
Ví dụ: Cho hình thang có cạnh đáy nhỏ a = 5cm, cạnh đáy lớn bằng b = 8 cm, chiều cao h = 4 cm. Diện tích hình thang này là?
Hướng dẫn giải
- Bước 1: Xác định giá trị a, b và h. Trong bài tâp này, a = 5cm, b = 8cm, h = 4cm.
- Bước 2: Áp dụng công thức tính diện tích ht:
$$S\;=\frac{(a+b)\;\times h}2$$
- Bước 3: Thay thế các giá trị a, b và h đã xác định ở bước 1 vào công thức, ta có:
$$S\;=\frac{(5+8)\;\times4}2=\;\frac{52}2\;=\;26\;cm^2$$
=> Vậy diện tích S ht = 26 cm2.
Lưu ý khi áp dụng công thức tính diện tích hình thang
Khi tính dt hình thang, cần nhớ một số điểm quan trọng sau:
- Xác định đúng độ dài của hai cạnh đáy (a, b) và chiều cao (h). Chú ý chúng phải cùng hệ đo lường.
- Chiều cao (h) là khoảng cách vuông góc từ một cạnh đáy đến cạnh đáy đối diện. Đừng nhầm lẫn với chiều dài cạnh bên không song song.
- Trong hình thang cân, bạn có thể áp dụng công thức thông thường hoặc tính chiều cao dựa trên tính chất hình học.
- Công thức tính diện tích cho hình thang và hình thang vuông tương tự nhau. Do đó, bạn có thể dễ dàng tìm chiều cao từ cạnh bên vuông góc với đáy.
- Khi làm các bài toán thực tế, đảm bảo sử dụng cùng hệ đo lường cho tất cả các giá trị và tránh nhầm lẫn giữa các hệ đo lường khác nhau.
Xem thêm: Tổng hợp các cách chứng minh hình thang chi tiết, dễ hiểu
Một số bài tập áp dụng công thức tính diện tích hình thang
Bài 1: Cho chiều dài 2 cạnh đáy và chiều cao lần lượt là 10cm, 12 cm, 7 cm, tính diện tích hình thang đó?
Cách giải
Sử dụng công thức:
$$S\;=\;h\;x\frac{a+b}2\;$$
ta có:
$$S\;=\frac{7\;x\;(10\;+\;12)}2=77cm^2\\\\$$
Bài 2: Một mảnh vườn hình thang có đáy lớn, đáy bé lần lượt là 20m và 24m. Sau này, người ta đã nới rộng 2 đáy lớn, đáy bé với số liệu lần lượt là 3m và 5m, diện tích lúc bấy giờ đã tăng thêm 38m2 so với ban đầu. Hỏi, diện tích ban đầu của khu vườn là bao nhiêu cm2?
Cách giải
Ta tính chiều cao mới của mảnh đất sau khi mở rộng:
$$h=\frac{S\times2}{a+b}=\;\frac{38\;\times x}{3+5}=9.5m\\$$
Vậy, diện tích mảnh đất ban đầu là:
$$S=\;9,5\;\times\frac{(20+24)}2=\;209m2$$
Đổi: 209 m2 = 2090000 cm2.
Bài 3: Khoảng cách giữa 2 đáy lớn, đáy bé của hình thang vuông là 20cm. Trong đó, đáy nhỏ bằng 1/3 đáy lớn. Được biết, diện tích của hình là 200cm2, vậy độ dài hai đáy của hình thang vuông đó là bao nhiêu?
Cách giải
Ta có tổng độ dài của 2 đáy là:
$$\frac{(200\;x\;2)\;}{20}\;=\;20\;cm$$
. Gọi độ dài dáy bé và đáy lớn lần lượt là x, y. Ta có: a = 1/3b và a+b = 20. Từ đó, tính được a = 5, b = 15.
Bài 4: Cho hình ABCD vuông tại A, có AB = 12 cm, CD = 15cm, AD = 8cm, hãy tính diện tích ABCD
Cách giải
Sử dụng công thức:
$$S\;=\;(AB\;+\;CD)\;x\;\frac{AD}2$$
ta có:
$$S=\;(12\;+\;15)\times\frac82=\;108\;cm2$$.
Đọc thêm: Dhnb hình thang là gì? Mẹo nhận biết đơn giản nhất
Ứng dụng thực tế của việc tính dt hình thang
Việc tính dt hình thang rất hữu ích và có nhiều ứng dụng thực tiễn:
- Trong kiến trúc và xây dựng: Dùng để tính diện tích sàn nhà từ kích thước cơ bản.
- Đo đạc đất đai: Xác định diện tích các khu vực đất hình thang.
- Phát triển kỹ năng toán học: Giúp rèn luyện tư duy logic và giải quyết vấn đề.
- Tính tổng quát: Cơ sở cho việc tính diện tích của các hình dạng phức tạp hơn như tam giác, bình hành.
Ví dụ:
- Một chiếc túi có đáy lớn 20 cm, đáy nhỏ 15 cm và chiều cao 30 cm. Vậy chiếc túi này có diện tích khoảng 525 cm².
- Tính chu vi và diện tích hình thang để tính lượng chất liệu cần thiết cho tấm thảm.

Trên đây là tổng hợp những công thức tính diện tích hình thang cũng như các bài tập minh hoạ. Hy vọng bài viết đã giúp bạn nắm được các cách giải bài tập cơ bản và nâng cao của dạng hình học này. Để lại bình luận bên dưới nếu bạn vẫn còn thắc mắc cần được giải đáp!




