Kiến thức và công thức về ba đường conic trong toán học cơ bản

Ba đường conic là những đường cong hình học quan trọng, hình thành từ giao điểm của mặt phẳng và mặt nón. Bài viết này sẽ giới thiệu phương trình, đặc điểm và ứng dụng thực tiễn của từng loại đường conic như parabol, elip và hyperbol. Từ đó, người đọc sẽ hiểu rõ hơn về sự liên hệ và tính chất của các đường conic trong hình học.

Ba đường conic là những đường cong hình học cơ bản được tạo thành từ giao tuyến của mặt phẳng và mặt nón tròn xoay

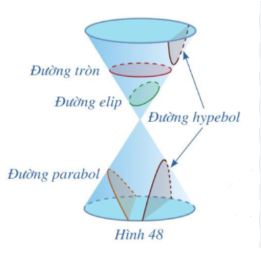
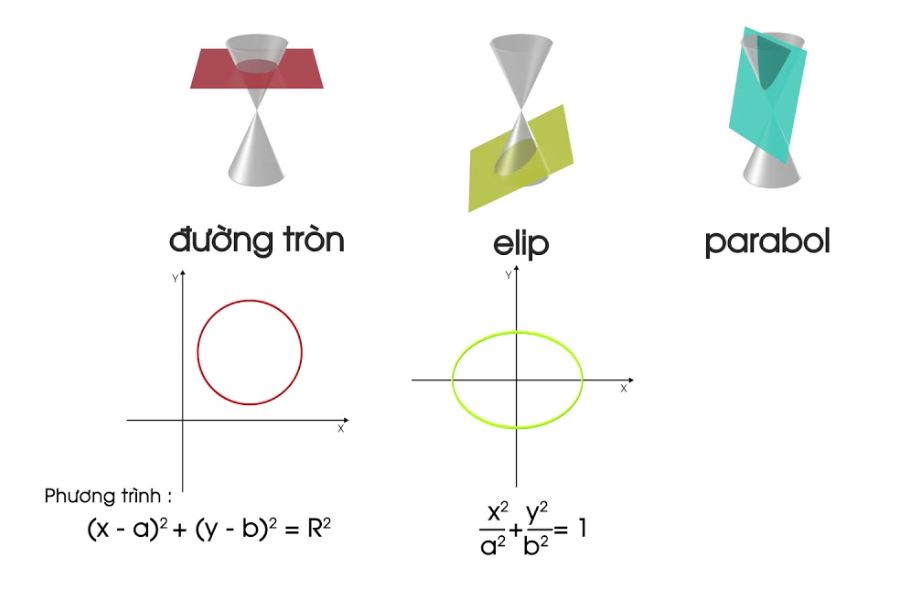
Trong Hình học phẳng, ba đường conic là những đường cong đặc biệt được tạo ra khi một mặt phẳng cắt một mặt nón tròn xoay theo các góc khác nhau. Chúng bao gồm đường tròn, elip và parabol – những hình dạng cơ bản mà ta thường gặp trong thực tế.

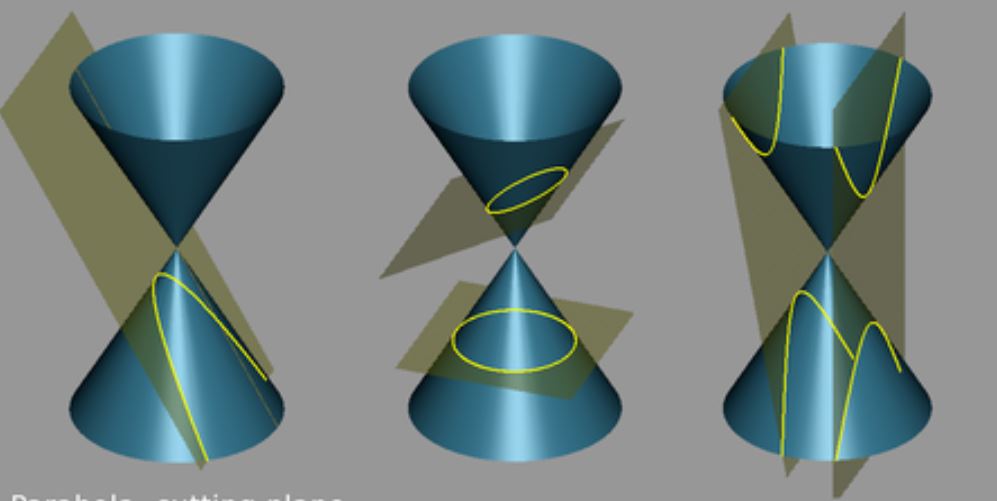
Mỗi đường cong trong 3 đường conic đều có những tính chất hình học độc đáo và ứng dụng riêng. Đường tròn xuất hiện khi mặt phẳng cắt vuông góc với trục của mặt nón. Elip hình thành khi mặt phẳng cắt nghiêng một góc với trục mặt nón. Parabol sinh ra khi mặt phẳng song song với một đường sinh của mặt nón.

Các đường conic không chỉ là những khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tiễn quan trọng. Chẳng hạn như quỹ đạo chuyển động của các hành tinh quanh Mặt Trời là elip, đường parabol mô tả quỹ đạo của vật bị ném xiên, hay hình dạng của ăng-ten parabol dùng trong truyền thông vệ tinh.

Phương trình tổng quát và đặc điểm của ba đường conic trong hệ tọa độ Descartes

Ba đường conic là những đường cong bậc hai được tạo thành từ giao điểm của mặt nón tròn xoay với mặt phẳng. Phương trình tổng quát của chúng trong hệ tọa độ Descartes có dạng: ax² + by² + 2hxy + 2gx + 2fy + c = 0, trong đó các hệ số a, b, c, f, g, h là các số thực và ít nhất một trong các hệ số a, b, h khác 0.

Mỗi đường conic đều có những đặc trưng riêng biệt về hình dạng và tính chất hình học. Việc phân loại các công thức 3 đường conic dựa vào mối quan hệ giữa các hệ số và định thức của ma trận hệ số. Điều này giúp xác định chính xác loại đường conic và các tham số đặc trưng của nó.

Phương trình chuẩn tắc của Parabol và các tính chất đặc trưng

Parabol là đường conic có phương trình chuẩn tắc dạng y² = 2px hoặc x² = 2py, với p là tham số dương. Đường cong này có một tiêu điểm và một đường chuẩn, khoảng cách từ một điểm bất kỳ trên parabol đến tiêu điểm luôn bằng khoảng cách từ điểm đó đến đường chuẩn.

Parabol có trục đối xứng song song với một trong hai trục tọa độ. Khi mở rộng vô hạn, các nhánh parabol tiến dần đến song song với trục đối xứng. Điểm đỉnh của parabol là điểm gần tiêu điểm nhất, cách tiêu điểm một khoảng p/2.

Phương trình chuẩn tắc của Elip và các đặc điểm hình học

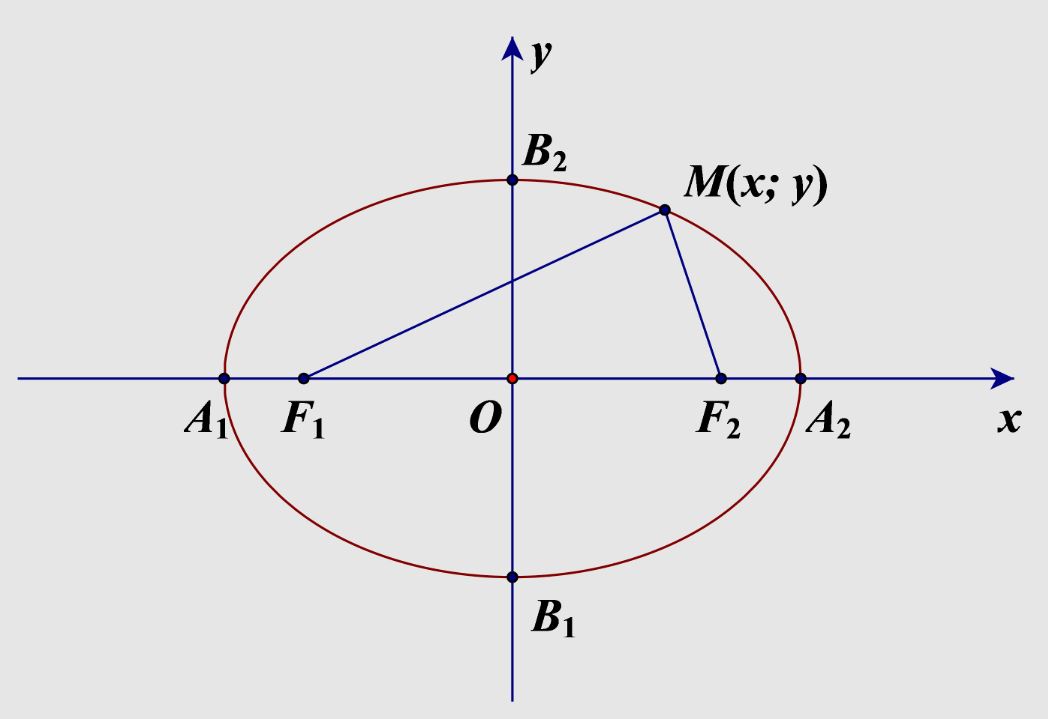
Elip có phương trình chuẩn tắc dạng x²/a² + y²/b² = 1, với a và b là các số dương. Đường cong này có hai tiêu điểm, tổng khoảng cách từ một điểm bất kỳ trên elip đến hai tiêu điểm luôn không đổi và bằng 2a.

Trục lớn của elip có độ dài 2a, trục nhỏ có độ dài 2b. Tâm elip nằm tại giao điểm của hai trục này. Độ lệch tâm e = c/a (với c² = a² – b²) là một đặc trưng quan trọng, cho biết mức độ “dẹt” của elip so với hình tròn.

Phương trình chuẩn tắc của Hyperbol và đặc điểm tiêu biểu

Đường hypebol có phương trình chuẩn tắc dạng x²/a² – y²/b² = 1 hoặc y²/a² – x²/b² = 1. Đây là đường cong có hai nhánh riêng biệt và hai tiêu điểm, hiệu khoảng cách từ một điểm bất kỳ trên hyperbol đến hai tiêu điểm luôn không đổi và bằng 2a.

Hyperbol có hai tiệm cận là hai đường thẳng đi qua tâm, các nhánh của hyperbol tiến dần đến các tiệm cận khi điểm trên đường cong di chuyển ra xa vô hạn. Độ lệch tâm e = c/a (với c² = a² + b²) luôn lớn hơn 1, phản ánh đặc điểm “mở” của hyperbol.

Các đường chuẩn của hyperbol là hai đường thẳng vuông góc với trục thực, cách tiêu

Các yếu tố hình học cơ bản của ba đường conic và mối liên hệ giữa chúng

Ba đường conic là những đường cong bậc hai được tạo thành từ giao tuyến của mặt nón tròn xoay với mặt phẳng. Chúng bao gồm parabol, elip và hyperbol – mỗi loại có những đặc điểm hình học riêng biệt nhưng vẫn có mối liên hệ chặt chẽ với nhau.

Khi nghiên cứu về lý thuyết 3 đường conic, ta thấy chúng đều có thể được biểu diễn dưới dạng phương trình bậc hai. Điều này cho phép 3 vecto đồng phẳng có thể áp dụng để mô tả các đặc trưng hình học của chúng một cách thống nhất.

Tiêu điểm và đường chuẩn của Parabol

Parabol có một tiêu điểm F và một đường chuẩn d. Mọi điểm trên parabol đều cách đều tiêu điểm và đường chuẩn. Đặc tính này tạo nên hình dạng đối xứng đặc trưng của parabol.

Khoảng cách từ tiêu điểm đến đường chuẩn được gọi là tham số p của parabol. Giá trị này quyết định độ “mở” của parabol – p càng lớn thì parabol càng mở rộng, p càng nhỏ thì parabol càng nhọn.

Tiêu điểm và trục của Elip

Elip có hai tiêu điểm F1 và F2 nằm trên trục lớn. Tổng khoảng cách từ mọi điểm trên elip đến hai tiêu điểm luôn bằng một hằng số 2a, với a là độ dài nửa trục lớn.

Trục lớn và trục nhỏ của elip tạo thành hai đường thẳng vuông góc với nhau đi qua tâm elip. Tỷ số giữa độ dài hai trục này xác định độ dẹt của elip. Khi hai trục bằng nhau, elip trở thành đường tròn.

Tiêu điểm và tiệm cận của Hyperbol

Hyperbol có hai tiêu điểm F1 và F2, và hiệu khoảng cách từ mọi điểm trên hyperbol đến hai tiêu điểm luôn bằng một hằng số 2a. Đặc điểm này tạo ra hai nhánh hyperbol đối xứng qua tâm.

Hyperbol có hai đường tiệm cận là hai đường thẳng mà các nhánh hyperbol tiến dần đến khi x tiến ra vô cùng. Góc giữa hai tiệm cận phụ thuộc vào tỷ số giữa các tham số a và b của hyperbol. Các tiệm cận đóng vai trò quan trọng trong việc xác định hình dạng tổng thể của hyperbol.

Sơ đồ tư duy tổng hợp về ba đường conic và ứng dụng trong thực tế

Ba đường conic là những đường cong hình học cơ bản được tạo ra từ việc cắt một mặt phẳng với một mặt nón tròn xoay. Các đường cong này bao gồm parabol, elip và hyperbol, mỗi loại đều có những đặc điểm và ứng dụng riêng biệt trong thực tế. Việc nắm vững sơ đồ tư duy ba đường conic giúp ta hiểu rõ hơn về mối liên hệ giữa toán học và các ứng dụng thực tiễn.

Để hiểu sâu hơn về cách áp dụng kiến thức này vào thực tế, bạn có thể tham khảo thêm tại Học Thế Nào. Dưới đây là phân tích chi tiết về ứng dụng của từng đường conic trong các lĩnh vực khác nhau.

Ứng dụng của Parabol trong kỹ thuật và kiến trúc

Parabol được ứng dụng rộng rãi trong thiết kế các công trình kiến trúc hiện đại. Theo kiến trúc sư Frank Gehry, đường cong parabol tạo nên sự cân bằng hoàn hảo giữa tính thẩm mỹ và độ bền vững của công trình.

Trong lĩnh vực kỹ thuật, parabol đóng vai trò quan trọng trong thiết kế đèn pha ô tô và đèn chiếu sáng. Nguyên lý phản xạ của parabol giúp tập trung ánh sáng theo hướng mong muốn, tạo hiệu quả chiếu sáng tối ưu.

Các ăng-ten parabol được sử dụng phổ biến trong truyền thông vệ tinh, với khả năng thu và phát sóng hiệu quả nhờ đặc tính hội tụ của đường cong này.

Ứng dụng của Elip trong thiên văn học và âm học

Trong thiên văn học, Johannes Kepler đã chứng minh rằng các hành tinh chuyển động theo quỹ đạo elip quanh Mặt Trời. Phát hiện này đã mở ra kỷ nguyên mới trong nghiên cứu vũ trụ và cơ học thiên thể.

Về mặt âm học, phòng thì thầm với thiết kế hình elip tạo ra hiện tượng âm thanh độc đáo. Khi người nói đứng tại một tiêu điểm, âm thanh sẽ được phản xạ và tập trung tại tiêu điểm còn lại, cho phép người nghe có thể nghe rõ dù ở khoảng cách xa.

Ứng dụng của Hyperbol trong định vị và truyền thông

Hyperbol được ứng dụng trong hệ thống định vị LORAN (Long Range Navigation), một công nghệ định vị vô tuyến được phát triển trong Thế chiến II. Nguyên lý hoạt động dựa trên sự chênh lệch thời gian của tín hiệu từ các trạm phát đến máy thu.

Trong lĩnh vực truyền thông, tháp làm mát hyperbol được thiết kế để tối ưu hóa quá trình trao đổi nhiệt. Theo nghiên cứu của Đại học MIT, hình dạng hyperbol giúp tăng hiệu suất làm mát lên đến 30% so với các thiết kế truyền thống.

Các kính thiên văn vô tuyến cũng sử dụng bề mặt phản xạ hyperbol để thu thập và xử lý tín hiệu từ vũ trụ một cách chính xác.

Phương pháp biến đổi và dịch chuyển ba đường conic trong mặt phẳng tọa độ

Các phép biến đổi và dịch chuyển ba đường conic trong mặt phẳng tọa độ là những công cụ quan trọng để nghiên cứu và phân tích hình học. Việc nắm vững các phép biến đổi này giúp ta dễ dàng xác định vị trí và hình dạng của đường conic sau khi thực hiện các phép biến đổi.

Để thực hiện chính xác các phép biến đổi, ta cần áp dụng các công thức lượng giác cơ bản như bài thơ lượng giác và các phương trình chuyển đổi tọa độ. Các phép biến đổi cơ bản bao gồm tịnh tiến, quay, đối xứng và vị tự.

Phép tịnh tiến và phép quay đường conic

Phép tịnh tiến đường conic được thực hiện bằng cách dịch chuyển tất cả các điểm của đường conic một khoảng cách không đổi theo một vector cho trước. Công thức tịnh tiến điểm (x,y) theo vector (a,b) là: x’ = x + a và y’ = y + b. Phép tịnh tiến không làm thay đổi hình dạng và kích thước của đường conic.

Phép quay đường conic quanh một điểm cố định O được thực hiện bằng cách quay tất cả các điểm của đường conic một góc α cho trước. Công thức quay điểm (x,y) quanh gốc tọa độ một góc α là: x’ = xcosα – ysinα và y’ = xsinα + ycosα. Phép quay chỉ thay đổi hướng của đường conic mà không làm thay đổi hình dạng và kích thước.

Phép đối xứng và phép vị tự đường conic

Phép đối xứng qua một đường thẳng hoặc một điểm là phép biến đổi đảo chiều của đường conic. Khi thực hiện phép đối xứng qua trục Ox, tọa độ y của mỗi điểm sẽ đổi dấu. Tương tự, đối xứng qua trục Oy sẽ đổi dấu tọa độ x. Phép đối xứng giữ nguyên hình dạng và kích thước của đường conic.

Phép vị tự với tâm O và tỷ số k là phép biến đổi làm thay đổi kích thước của đường conic theo một tỷ lệ không đổi k. Nếu k > 1, đường conic sẽ giãn ra, nếu 0 < k < 1, đường conic sẽ co lại. Công thức vị tự điểm (x,y) với tâm O(0,0) và tỷ số k là: x’ = kx và y’ = ky. Phép vị tự chỉ thay đổi kích thước mà không làm thay đổi hình dạng của đường conic.

Kết luận về ba đường conic cho thấy rằng chúng không chỉ là những hình học trừu tượng mà còn có ứng dụng quan trọng trong nhiều lĩnh vực. Phương trình, đặc điểm và cách biến đổi của chúng đóng vai trò quan trọng trong lý thuyết hình học cũng như trong thực tiễn, từ kỹ thuật đến thiên văn học. Bạn nên nắm vững các khái niệm này để có thể áp dụng hiệu quả vào học tập và thực tiễn.