Tính diện tích hình viên phân: Công thức, ví dụ và ứng dụng thực tiễn

Diện tích hình viên phân là phần diện tích được giới hạn bởi một cung tròn và dây cung tương ứng. Nắm rõ diện tích hình viên phân giúp học sinh lớp 9 giải quyết các bài toán liên quan. Tại bài viết này, chúng tôi sẽ cung cấp công thức, hướng dẫn cụ thể và các ứng dụng thú vị của hình học này trong thực tiễn.

Diện tích hình viên phân là phần diện tích được giới hạn bởi một cung tròn và dây cung tương ứng

Trong hình học, diện tích hình viên phân được xác định là phần diện tích nằm giữa một cung tròn và dây cung tương ứng của nó. Đây là một khái niệm quan trọng khi nghiên cứu về hình tròn và các yếu tố liên quan.

Hình viên phân có đặc điểm là luôn được giới hạn bởi hai thành phần chính: một cung tròn phía trên và một đoạn thẳng (dây cung) phía dưới. Khi cung tròn càng lớn so với dây cung, diện tích của hình viên phân càng tăng và ngược lại.

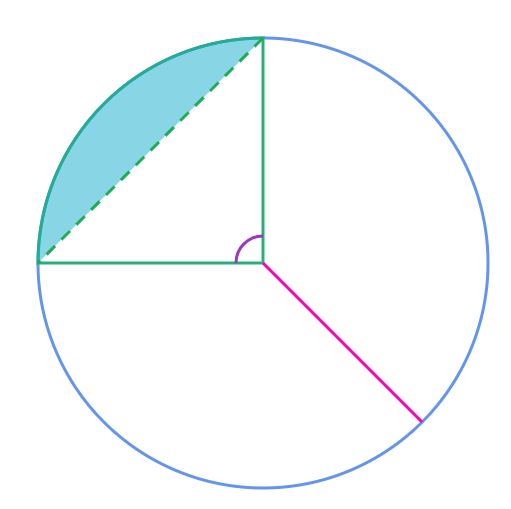
Để tính được diện tích của hình viên phân, cần xác định diện tích của hình quạt tròn tương ứng với cung tròn, sau đó trừ đi diện tích của tam giác được tạo bởi tâm và hai đầu mút của dây cung. Công thức này giúp tính chính xác diện tích phần còn lại – chính là diện tích hình viên phân cần tìm.

Công thức tính diện tích hình viên phân và các thành phần liên quan

Trong toán hình học phẳng, việc tính diện tích hình viên phân đòi hỏi sự hiểu biết về các thành phần cấu tạo và mối quan hệ giữa chúng. Công thức tính diện tích hình viên phân được xây dựng dựa trên các yếu tố hình học cơ bản như cung tròn, dây cung và góc ở tâm.

Để áp dụng công thức một cách chính xác, cần nắm vững các khái niệm về hình viên phân như phần diện tích được giới hạn bởi cung tròn và dây cung. Việc xác định chính xác các thành phần sẽ giúp quá trình tính toán trở nên dễ dàng và chính xác hơn.

Các yếu tố cần biết để tính diện tích hình viên phân

Trước khi áp dụng công thức, việc xác định các yếu tố của hình viên phân là bước quan trọng đầu tiên. Bán kính của đường tròn (R) và độ dài dây cung (d) là hai thông số cơ bản cần được đo lường chính xác.

Góc ở tâm (α) tạo bởi hai bán kính đi qua hai đầu dây cung cũng đóng vai trò quan trọng. Góc này được đo bằng radian và có mối liên hệ trực tiếp với diện tích phần hình viên phân.

Độ cao của hình viên phân (h) – khoảng cách từ tâm đường tròn đến dây cung – cũng là một yếu tố cần được xác định để tính toán chính xác.

Công thức tổng quát tính diện tích hình viên phân

Diện tích hình viên phân được tính bằng hiệu số giữa diện tích hình quạt tròn và diện tích tam giác tạo bởi tâm và hai đầu dây cung. Công thức tổng quát được biểu diễn như sau:

S = (α/2)R² – (d×h)/2

Trong đó α là góc ở tâm (tính bằng radian), R là bán kính đường tròn, d là độ dài dây cung và h là độ cao của hình viên phân.

Các trường hợp đặc biệt khi tính diện tích hình viên phân

Khi góc ở tâm bằng π radian (180 độ), hình viên phân trở thành nửa đường tròn. Trong trường hợp này, diện tích được tính đơn giản hơn với công thức S = πR²/2.

Nếu góc ở tâm nhỏ hơn π/2 radian (90 độ), diện tích hình viên phân sẽ nhỏ hơn 1/4 diện tích đường tròn. Điều này thường gặp trong các bài toán thực tế về thiết kế và xây dựng.

Trường hợp góc ở tâm lớn hơn π radian tạo ra hình viên phân lớn, cách tính diện tích hình viên phân sẽ cần điều chỉnh dấu trong công thức để phản ánh đúng phần diện tích cần tính.

Hướng dẫn giải các bài toán về diện tích hình viên phân trong chương trình lớp 9

Việc tính diện tích hình viên phân lớp 9 đòi hỏi học sinh nắm vững kiến thức về hình học và các công thức tính diện tích cơ bản. Phần này sẽ giới thiệu các phương pháp và kỹ thuật giải quyết bài toán một cách hiệu quả.

Phương pháp giải bài toán cơ bản

Để giải các bài toán về diện tích hình viên phân, cần xác định rõ các yếu tố then chốt. Trước tiên, phân tích kỹ hình vẽ và các dữ kiện đã cho trong đề bài. Sau đó, vận dụng các công thức tính diện tích phù hợp với từng phần của hình viên phân.

Việc chia nhỏ hình viên phân thành các hình cơ bản quen thuộc như tam giác, hình thang hay hình chữ nhật sẽ giúp bài toán trở nên đơn giản hơn. Cuối cùng, tổng hợp kết quả từ các phần để có được diện tích toàn bộ hình viên phân.

Các dạng bài tập thường gặp

Trong chương trình toán lớp 9, diện tích hình viên phân tính toán thường xuất hiện dưới nhiều dạng khác nhau. Phổ biến nhất là các bài toán yêu cầu tính diện tích phần giao của hai hình, hoặc hiệu diện tích giữa hai hình viên phân.

Một dạng bài tập khác thường gặp là tìm diện tích phần còn lại của hình viên phân sau khi đã cắt bỏ một phần. Dạng này đòi hỏi kỹ năng phân tích hình học tốt và khả năng vận dụng linh hoạt các công thức.

Ngoài ra còn có các bài toán về tỷ số diện tích giữa các phần của hình viên phân, hoặc bài toán chứng minh sự bằng nhau về diện tích giữa các phần.

Bài tập mẫu có lời giải chi tiết

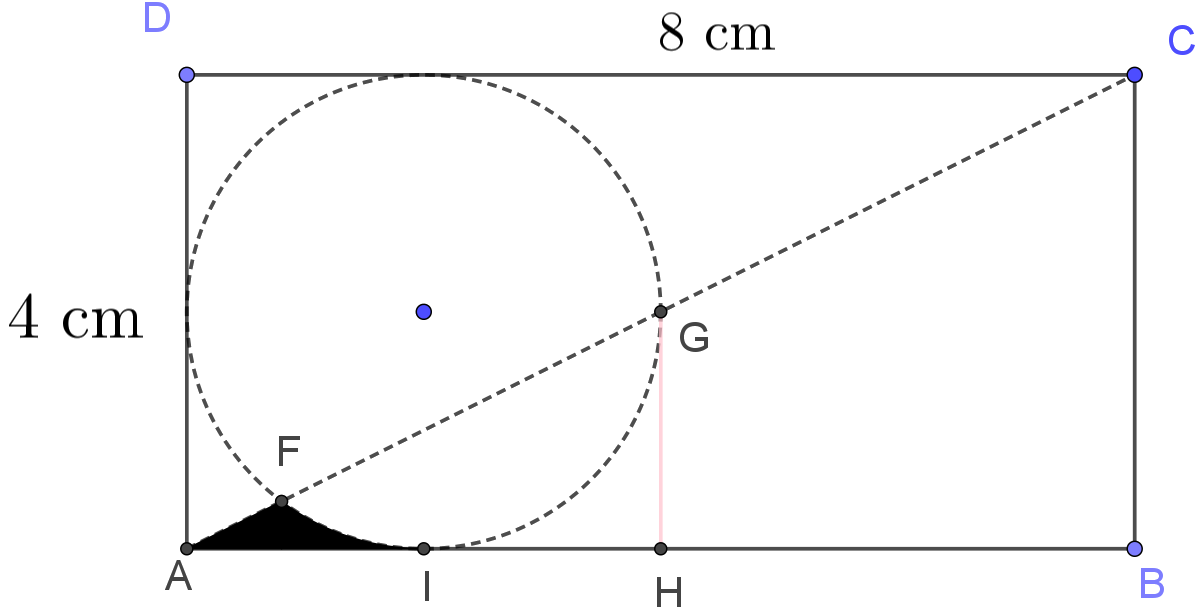
Bài toán: Cho hình viên phân gồm một hình tròn bán kính R và một tam giác đều nội tiếp. Tính diện tích phần còn lại của hình tròn nằm ngoài tam giác.

Lời giải:

• Bước 1: Tính diện tích hình tròn S1 = πR²
• Bước 2: Tính diện tích tam giác đều nội tiếp S2 = (R²√3)/4
• Bước 3: Diện tích phần cần tìm = S1 – S2 = πR² – (R²√3)/4

Một ví dụ khác về bài toán phức tạp hơn là tính diện tích phần giao của hai hình tròn bằng nhau có bán kính R, tâm cách nhau một khoảng d < 2R. Bài toán này đòi hỏi vận dụng kiến thức về góc cung và diện tích hình quạt tròn.

Ứng dụng thực tiễn của việc tính diện tích hình viên phân

Ứng dụng diện tích hình viên phân có vai trò quan trọng trong nhiều lĩnh vực thực tiễn, từ kiến trúc xây dựng đến thiết kế và khoa học kỹ thuật. Việc tính toán chính xác diện tích hình viên phân giúp tối ưu hóa các thiết kế phức tạp, tiết kiệm nguyên vật liệu và nâng cao tính thẩm mỹ cho công trình.

Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc, việc tính diện tích hình viên phân được áp dụng rộng rãi để thiết kế mái vòm, cầu thang xoắn ốc và các cấu trúc cong. Công trình Opera House Sydney là một ví dụ điển hình, với hệ thống mái vòm được thiết kế dựa trên các phép tính diện tích hình viên phân phức tạp.

Các kiến trúc sư thường sử dụng phương pháp này để tối ưu hóa không gian và đảm bảo tính ổn định của công trình. Theo số liệu từ Hiệp hội Kiến trúc sư Quốc tế (UIA), khoảng 40% các công trình hiện đại có ứng dụng tính toán diện tích hình viên phân trong thiết kế.

Ứng dụng trong thiết kế và mỹ thuật

Nghệ thuật đương đại thường xuyên sử dụng các đường cong và hình dạng phi tuyến tính, đòi hỏi việc tính toán diện tích hình viên phân để tạo ra tác phẩm hoàn chỉnh. Các nhà thiết kế đồ họa áp dụng nguyên lý này trong việc tạo logo, banner và các ấn phẩm quảng cáo.

Một ví dụ nổi bật là logo của hãng Nike – được thiết kế bởi Carolyn Davidson năm 1971, sử dụng đường cong Bezier và tính toán diện tích hình viên phân để tạo ra biểu tượng “swoosh” mang tính biểu tượng. Phương pháp này cũng được áp dụng rộng rãi trong thiết kế nội thất và trang trí không gian.

Ứng dụng trong các lĩnh vực khoa học kỹ thuật

Trong công nghiệp chế tạo, việc tính diện tích hình viên phân đóng vai trò then chốt trong thiết kế các bộ phận máy móc có hình dạng phức tạp. Ngành hàng không vũ trụ sử dụng phương pháp này để tối ưu hóa thiết kế cánh máy bay và tính toán lực cản không khí.

Theo nghiên cứu của NASA, việc áp dụng chính xác các phép tính diện tích hình viên phân trong thiết kế cánh máy bay có thể giúp tiết kiệm đến 15% nhiên liệu. Trong y học, kỹ thuật này được sử dụng để tính toán diện tích bề mặt các cơ quan nội tạng, hỗ trợ chẩn đoán và điều trị bệnh chính xác hơn.

Các phương pháp và mẹo tính nhanh diện tích hình viên phân

Việc tính toán diện tích hình viên phân công thức đòi hỏi sự chính xác và phương pháp phù hợp. Các phương pháp tính nhanh giúp tiết kiệm thời gian mà vẫn đảm bảo độ chính xác cần thiết trong nhiều bài toán thực tế.

Một số ví dụ về diện tích hình viên phân điển hình như tính diện tích mảnh đất không đều, diện tích mặt cắt ngang của vật thể hay diện tích các hình phẳng phức tạp trong thiết kế. Việc áp dụng các phương pháp tính nhanh phù hợp sẽ giúp đơn giản hóa quá trình tính toán.

Cách ước lượng diện tích hình viên phân

Phương pháp ước lượng diện tích hình viên phân thường được thực hiện bằng cách chia nhỏ hình thành các phần đơn giản hơn. Việc phân chia cần dựa trên các đặc điểm hình học của hình viên phân để tối ưu quá trình tính toán.

Kỹ thuật ước lượng bằng lưới ô vuông cũng là một phương pháp hiệu quả. Bằng cách đếm số ô vuông hoàn chỉnh và ước tính các phần lẻ, ta có thể xác định gần đúng diện tích cần tính.

Trong thực tế, việc kết hợp nhiều phương pháp ước lượng khác nhau sẽ cho kết quả chính xác hơn. Điều này đặc biệt quan trọng khi làm việc với các hình viên phân phức tạp.

Sử dụng công cụ hỗ trợ tính toán

Các phần mềm chuyên dụng như AutoCAD, GeoGebra hay các ứng dụng tính toán diện tích trên điện thoại di động có thể hỗ trợ đắc lực trong việc tính diện tích hình viên phân. Những công cụ này cung cấp các tính năng đo đạc và tính toán tự động, giúp tăng độ chính xác và tiết kiệm thời gian.

Bên cạnh đó, việc sử dụng máy tính khoa học với các chức năng tích phân cũng rất hữu ích. Nhiều máy tính hiện đại có thể thực hiện các phép tính phức tạp liên quan đến diện tích hình viên phân một cách nhanh chóng.

Các lưu ý quan trọng khi tính diện tích hình viên phân

Khi tính toán diện tích hình viên phân, cần đặc biệt chú ý đến việc xác định chính xác các điểm đặc biệt và đường biên của hình. Sai số nhỏ trong quá trình đo đạc có thể dẫn đến kết quả sai lệch đáng kể.

Việc kiểm tra kết quả bằng nhiều phương pháp khác nhau là rất quan trọng. So sánh kết quả tính toán với các giá trị tham chiếu hoặc ước lượng ban đầu giúp phát hiện sớm các sai sót.

Ngoài ra, cần lưu ý đến đơn vị đo lường và quy đổi đơn vị phù hợp. Trong nhiều trường hợp, việc chuyển đổi không chính xác giữa các đơn vị có thể gây ra sai lệch lớn trong kết quả cuối cùng.

Diện tích hình viên phân là một khái niệm quan trọng trong hình học, giúp học sinh lớp 9 làm quen với các bài toán liên quan đến hình tròn. Việc hiểu rõ diện tích hình viên phân không chỉ giúp giải quyết các bài tập trong sách giáo khoa mà còn áp dụng trong các trường hợp thực tiễn như kiến trúc hay thiết kế. Hãy vận dụng các công thức và cách tính đã học để nâng cao kỹ năng toán học của bạn.