Cách tính diện tích ngũ giác đều với công thức và bài tập minh họa chi tiết

Diện tích ngũ giác đều là một khái niệm quan trọng trong hình học. Bài viết này cung cấp công thức, phương pháp và ứng dụng cụ thể để tính diện tích ngũ giác đều. Bạn sẽ tìm thấy các bước thực hiện chi tiết, bài tập cơ bản và nâng cao, giúp tăng cường kỹ năng toán học của mình.

Diện tích ngũ giác đều và các thành phần cơ bản

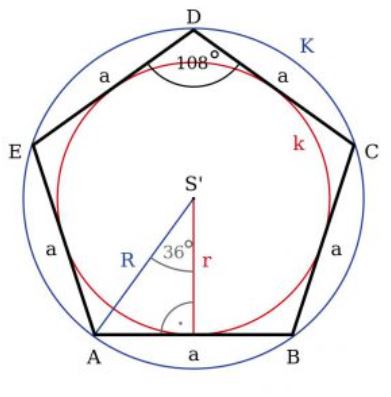
Để tính được diện tích ngũ giác đều, trước tiên cần hiểu rõ về cấu trúc hình học của nó. ngũ giác đều là gì là một đa giác có 5 cạnh bằng nhau và 5 góc bằng nhau, mỗi góc có số đo 108 độ. Đây là một trong những hình đa giác đều cơ bản trong hình học phẳng.

Diện tích của ngũ giác đều được tính dựa trên các thành phần cơ bản như cạnh, đường cao và bán kính đường tròn ngoại tiếp. Công thức tổng quát để tính diện tích là nhân độ dài cạnh với nửa chu vi và bán kính đường tròn nội tiếp. Ngoài ra, có thể sử dụng công thức khác dựa vào độ dài cạnh và góc giữa hai cạnh kề.

Khi áp dụng vào thực tế, việc tính toán diện tích ngũ giác đều thường được sử dụng trong thiết kế kiến trúc, xây dựng và nghệ thuật. Ví dụ như thiết kế các công trình có mặt bằng hình ngũ giác đều như đài tưởng niệm, nhà thờ hay các công trình văn hóa độc đáo. Việc nắm vững cách tính diện tích sẽ giúp đảm bảo tính chính xác trong quá trình thiết kế và thi công.

Công thức tính diện tích ngũ giác đều và cách áp dụng

Việc tính diện tích ngũ giác đều là một bài toán quan trọng trong công thức hình học phẳng. Ngũ giác đều là hình đa giác có 5 cạnh bằng nhau và 5 góc bằng nhau, tạo nên một hình đối xứng hoàn hảo.

Để tính chính xác diện tích của hình ngũ giác đều, ta cần nắm vững công thức tổng quát và các bước thực hiện cụ thể. Việc áp dụng đúng phương pháp sẽ giúp đạt kết quả chính xác và tiết kiệm thời gian.

Công thức tổng quát tính diện tích ngũ giác đều

Công thức tính diện tích ngũ giác đều được biểu diễn như sau:
S = (a² × √(25 + 10√5))/4

Trong đó:

• S là diện tích ngũ giác đều
• a là độ dài cạnh của ngũ giác đều
• √(25 + 10√5) là hằng số ≈ 6.881909602355868

Công thức này được xây dựng dựa trên các tính chất đặc biệt của ngũ giác đều, kết hợp với các phép tính lượng giác và đại số.

Các bước tính diện tích ngũ giác đều

Để tính diện tích ngũ giác đều một cách chính xác, ta thực hiện theo trình tự:

Bước 1: Xác định độ dài cạnh a của ngũ giác đều từ dữ kiện đề bài

Bước 2: Bình phương độ dài cạnh a để có a²

Bước 3: Tính √(25 + 10√5) ≈ 6.881909602355868

Bước 4: Nhân kết quả từ bước 2 với kết quả bước 3

Bước 5: Chia kết quả cho 4 để có diện tích cuối cùng

Ví dụ minh họa cách tính

Giả sử có một ngũ giác đều có cạnh a = 6cm, ta tính diện tích như sau:

a² = 6² = 36 (cm²)
√(25 + 10√5) ≈ 6.881909602355868
S = (36 × 6.881909602355868)/4
S ≈ 61.937 (cm²)

Kết quả này có thể kiểm chứng bằng phần mềm GeoGebra – công cụ được các giáo viên toán học tin dùng. Việc làm tròn số thập phân tùy thuộc vào yêu cầu độ chính xác của bài toán.

Phương pháp tính diện tích ngũ giác không đều

Cách tính diện tích hình ngũ giác không đều là phương pháp phân chia hình ngũ giác thành các tam giác nhỏ hơn, sau đó tính tổng diện tích các tam giác đó. Phương pháp này giúp đơn giản hóa việc tính toán cho các hình ngũ giác phức tạp, không có công thức trực tiếp.

Tính diện tích hình ngũ giác​ là một kỹ năng quan trọng trong hình học phẳng. Để thực hiện chính xác, cần nắm vững cách phân chia hình và áp dụng công thức tính diện tích tam giác cơ bản.

Phân chia ngũ giác thành các tam giác

Để phân chia ngũ giác thành các tam giác, cần chọn một đỉnh làm gốc và vẽ các đường chéo từ đỉnh đó đến các đỉnh không liền kề. Phương pháp này sẽ tạo ra 3 tam giác nhỏ hơn.

Khi thực hiện phân chia, nên chọn đỉnh sao cho các đường chéo không cắt nhau bên trong hình ngũ giác. Điều này giúp việc tính toán trở nên đơn giản và chính xác hơn.

Một nguyên tắc quan trọng là đảm bảo các tam giác được tạo thành không chồng lấn lên nhau và phủ kín toàn bộ diện tích của hình ngũ giác ban đầu.

Tính tổng diện tích các tam giác thành phần

Sau khi phân chia thành công, tiến hành tính diện tích từng tam giác riêng biệt. Với mỗi tam giác, có thể áp dụng các công thức tính diện tích phù hợp như:

• Công thức cơ bản: S = (a × h)/2 (với a là độ dài cạnh đáy, h là chiều cao)
• Công thức Heron: S = √(p(p-a)(p-b)(p-c)) (với p là nửa chu vi)
• Công thức lượng giác: S = (1/2) × a × b × sin(C)

Diện tích ngũ giác sẽ bằng tổng diện tích của 3 tam giác thành phần. Việc kiểm tra kết quả có thể thực hiện bằng cách so sánh với phép đo trực tiếp hoặc sử dụng phần mềm hỗ trợ tính toán.

Độ chính xác của kết quả phụ thuộc vào việc đo đạc các cạnh và góc của từng tam giác thành phần. Do đó, cần thực hiện cẩn thận từng bước tính toán để đảm bảo kết quả cuối cùng chính xác.

Đặc điểm và tính chất của ngũ giác đều

Ngũ giác đều là một đa giác đều có 5 cạnh và 5 góc bằng nhau. Đặc điểm ngũ giác đều nổi bật với tính đối xứng hoàn hảo và các yếu tố hình học đồng nhất. Hình dạng này thường xuất hiện trong tự nhiên và kiến trúc, từ hoa mai đến các công trình nổi tiếng như Lầu Năm Góc (Pentagon).

Các cạnh và góc bằng nhau

Trong ngũ giác đều, 5 cạnh có độ dài bằng nhau và 5 góc đều bằng 108°. Tính chất này tạo nên sự cân đối hoàn hảo cho hình. Khi vẽ các đường thẳng nối từ tâm đến các đỉnh, ta được 5 tam giác cân bằng nhau, tạo thành dãy tỉ số bằng nhau giữa các cạnh và đường cao.

Mối quan hệ giữa các cạnh và góc trong ngũ giác đều tuân theo quy luật chặt chẽ. Tổng số đo các góc trong luôn bằng 540°, được tính theo công thức (n-2) × 180° với n = 5.

Đường cao và đường chéo

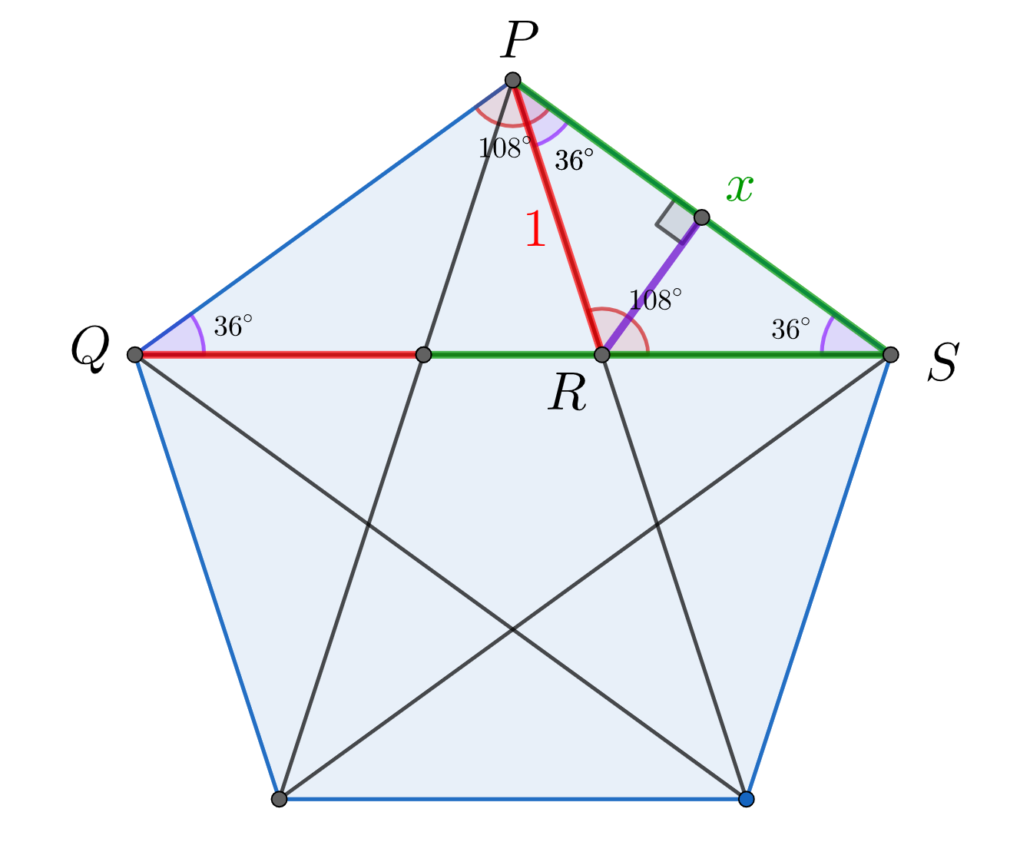
Đường cao trong ngũ giác đều được vẽ từ tâm vuông góc với cạnh. Tất cả đường cao đều bằng nhau và chia các cạnh thành hai phần bằng nhau. Ngũ giác đều có 5 đường chéo, tạo thành một ngôi sao năm cánh khi được vẽ đầy đủ.

Các đường chéo của ngũ giác đều cắt nhau tại các điểm tạo thành một ngũ giác đều nhỏ hơn ở bên trong. Diện tích ngũ giác đều có thể được tính dựa trên độ dài cạnh và đường cao.

Tâm đối xứng

Tâm đối xứng của ngũ giác đều là điểm giao nhau của các đường phân giác góc. Điểm này cũng chính là tâm của đường tròn ngoại tiếp và nội tiếp của ngũ giác. Từ tâm đối xứng, ta có thể xoay hình một góc 72° (360°/5) để được hình trùng khít với hình ban đầu.

Tính chất đối xứng này làm cho ngũ giác đều trở thành một trong những hình học hoàn hảo nhất trong toán học và thiết kế. Mọi điểm trên ngũ giác đều cách đều tâm đối xứng, tạo nên sự cân bằng tuyệt đối.

Ứng dụng và bài tập về diện tích ngũ giác đều

Việc tính toán bài tập diện tích ngũ giác đều đòi hỏi sự hiểu biết vững chắc về các công thức và tính chất hình học. Để giải quyết các bài toán phức tạp, cần nắm rõ mối liên hệ giữa các yếu tố như cạnh, đường cao, đường chéo và góc của ngũ giác đều.

Khi áp dụng tính chất hình chóp tứ giác đều và thể tích khối chóp tứ giác đều, ta có thể giải quyết nhiều dạng toán về diện tích ngũ giác đều một cách hiệu quả. Các bài tập được chia thành nhiều cấp độ khác nhau để phù hợp với trình độ người học.

Bài tập cơ bản

Các bài tập cơ bản thường yêu cầu tính diện tích ngũ giác đều khi biết độ dài cạnh hoặc bán kính đường tròn ngoại tiếp. Đây là nền tảng quan trọng giúp người học làm quen với các công thức tính toán cơ bản.

Một số bài tập điển hình yêu cầu xác định diện tích ngũ giác đều khi biết độ dài đường cao hoặc bán kính đường tròn nội tiếp. Những bài toán này giúp rèn luyện kỹ năng áp dụng công thức và tư duy logic.

Bài tập nâng cao

Bài tập nâng cao thường kết hợp kiến thức về ngũ giác đều với các hình khối trong không gian. Việc tính toán diện tích mặt đáy của lăng trụ ngũ giác đều hoặc hình chóp ngũ giác đều đòi hỏi sự hiểu biết sâu sắc về mối quan hệ không gian.

Các bài toán phức tạp có thể yêu cầu tìm diện tích ngũ giác đều khi biết tỉ số giữa các yếu tố như đường chéo và cạnh. Những dạng bài này rèn luyện khả năng phân tích và giải quyết vấn đề.

Phương pháp giải nhanh

Phương pháp giải nhanh đầu tiên là nhận diện các yếu tố đã cho trong đề bài và áp dụng công thức phù hợp. Việc ghi nhớ các công thức quan trọng giúp tiết kiệm thời gian giải toán đáng kể.

Kỹ thuật vẽ hình phụ và chia nhỏ ngũ giác thành các tam giác đều cũng là một phương pháp hiệu quả. Cách này giúp đơn giản hóa bài toán và tìm ra lời giải nhanh chóng.

Sử dụng tính chất đối xứng của ngũ giác đều để rút gọn các bước tính toán là một chiến thuật hữu ích. Phương pháp này đặc biệt phù hợp với các bài toán liên quan đến góc và đường chéo.

So sánh cách tính diện tích ngũ giác đều và không đều

Việc so sánh ngũ giác đều và không đều về mặt tính diện tích có những điểm khác biệt đáng chú ý. Với ngũ giác đều, ta có thể áp dụng công thức đơn giản do tính đối xứng và đều đặn của hình. Ngược lại, ngũ giác không đều đòi hỏi phương pháp phức tạp hơn như chia thành các tam giác nhỏ để tính.

Khi tính diện tích hình ngũ giác, phương pháp phổ biến là chia thành các tam giác và cộng diện tích các tam giác lại. Tuy nhiên, với ngũ giác đều ta có thể áp dụng trực tiếp công thức S = (5a²)/(4.tan36°) với a là độ dài cạnh. Tương tự như cách tính Diện tích hình lục giác đều, việc có công thức riêng giúp đơn giản hóa quá trình tính toán.

Điểm giống và khác nhau

Về điểm giống nhau, cả hai loại ngũ giác đều có 5 cạnh và 5 góc, tổng số đo các góc trong đều bằng 540°. Cả hai đều có thể tính diện tích bằng cách chia thành các tam giác nhỏ hơn.

Về khác biệt, ngũ giác đều có các cạnh bằng nhau và các góc bằng nhau (mỗi góc 108°), trong khi ngũ giác không đều có độ dài cạnh và số đo góc khác nhau. Điều này dẫn đến sự khác biệt trong cách tiếp cận tính diện tích của hai loại hình.

Lợi thế khi tính diện tích ngũ giác đều

Ngũ giác đều mang lại nhiều thuận lợi trong quá trình tính toán diện tích. Với tính chất đối xứng, ta có thể vẽ được đường cao từ tâm đến các cạnh đều bằng nhau, giúp việc tính toán trở nên đơn giản hơn.

Việc có sẵn công thức tính diện tích dựa vào độ dài cạnh giúp tiết kiệm thời gian và giảm thiểu sai sót trong quá trình tính. Không cần phải đo đạc nhiều kích thước hay thực hiện nhiều phép tính phức tạp như với ngũ giác không đều.

Ngoài ra, tính chất đều đặn còn giúp dễ dàng kiểm tra kết quả thông qua việc so sánh với các công thức khác hoặc phương pháp chia tam giác, đảm bảo độ chính xác của kết quả tính toán.

Cuối cùng, việc nắm rõ công thức tính diện tích ngũ giác đều là rất quan trọng để giải quyết các bài toán liên quan. Qua bài viết, bạn đã tìm hiểu về đặc điểm, cách tính và ứng dụng thực tế của ngũ giác đều trong hình học. Hy vọng rằng những kiến thức này sẽ giúp bạn tự tin hơn khi gặp các bài tập về diện tích ngũ giác trong tương lai.