Thể tích khối chóp tứ giác đều: Công thức, cách tính và ứng dụng thực tế

Thể tích khối chóp tứ giác đều là một trong những khái niệm quan trọng trong hình học không gian. Bài viết này sẽ cung cấp công thức tính, cách áp dụng và hướng dẫn thực hành để bạn có thể hiểu rõ hơn về loại hình chóp này. Hãy cùng khám phá để nâng cao kiến thức toán học của bạn!

Thể tích khối chóp tứ giác đều và các đặc điểm cơ bản

Khối chóp tứ giác đều là một khối đa diện có đáy là hình vuông và các mặt bên là các tam giác đều bằng nhau. Đây là một trong những hình khối quan trọng trong hình học không gian với nhiều ứng dụng thực tiễn trong kiến trúc và xây dựng.

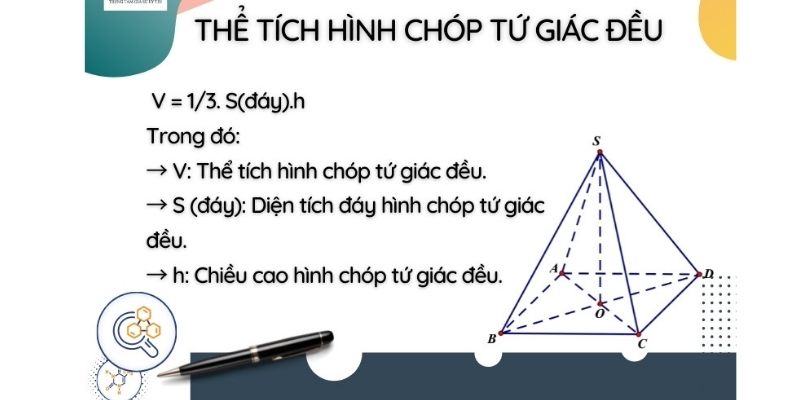
Để tính thể tích khối chóp tứ giác đều, ta áp dụng công thức V = (1/3) × S × h, trong đó S là diện tích đáy và h là chiều cao của khối chóp. Công thức này được phát triển từ định lý cơ bản về thể tích khối chóp, theo đó thể tích của một khối chóp bằng một phần ba tích của diện tích đáy và chiều cao.

Hình chóp tứ giác đều có một số tính chất đặc biệt giúp việc tính toán trở nên thuận tiện hơn. Các cạnh bên của khối chóp bằng nhau, các mặt bên có diện tích bằng nhau và tạo với mặt đáy một góc nghiêng bằng nhau. Điều này làm cho khối chóp tứ giác đều trở thành một hình khối có tính đối xứng cao và thường được sử dụng làm mẫu trong giảng dạy hình học không gian.

Khi áp dụng vào thực tế, các công trình kiến trúc như mái tháp, đỉnh kim tự tháp thường được thiết kế dựa trên nguyên lý của khối chóp tứ giác đều. Ví dụ điển hình là các kim tự tháp ở Ai Cập, với tỷ lệ giữa chiều cao và cạnh đáy được tính toán chính xác để tạo nên sự cân đối hoàn hảo.

Công thức tính thể tích khối chóp tứ giác đều và cách áp dụng

Để tính chính xác thể tích khối chóp tứ giác đều, cần nắm vững công thức và phương pháp áp dụng phù hợp. Khối chóp tứ giác đều là một khối đa diện có đáy là hình vuông và các mặt bên là các tam giác đều. Việc tính toán thể tích của khối này đòi hỏi sự hiểu biết về các yếu tố cấu thành và mối quan hệ giữa chúng.

Công thức tổng quát tính thể tích khối chóp tứ giác đều

Công thức tính thể tích chóp tứ giác đều được xác định bằng tích của diện tích đáy và một phần ba chiều cao. Cụ thể, công thức thể tích hình chóp là V = (1/3) × S × h, trong đó S là diện tích đáy và h là chiều cao của khối chóp. Với khối chóp tứ giác đều, diện tích đáy S = a², với a là cạnh đáy.

Khi áp dụng công thức, cần lưu ý rằng chiều cao h phải là đường vuông góc từ đỉnh chóp đến mặt phẳng đáy. Chiều cao này khác với độ dài cạnh bên của khối chóp, và việc phân biệt rõ hai yếu tố này sẽ giúp tránh sai sót trong quá trình tính toán.

Các bước tính thể tích khối chóp tứ giác đều

Bước đầu tiên là xác định cạnh đáy a của khối chóp để tính diện tích đáy S = a². Tiếp theo, xác định chiều cao h của khối chóp bằng cách đo hoặc tính toán dựa trên các yếu tố đã biết.

Sau khi có đủ các thông số cần thiết, áp dụng công thức V = (1/3) × a² × h để tính thể tích. Việc thực hiện theo trình tự sẽ giúp quá trình tính toán trở nên chính xác và hiệu quả hơn.

Ví dụ minh họa cách tính

Cho một khối chóp tứ giác đều có cạnh đáy a = 6cm và chiều cao h = 8cm. Cách tính thể tích chóp tứ giác đều như sau:

Diện tích đáy S = a² = 6² = 36 cm²
Thể tích V = (1/3) × S × h = (1/3) × 36 × 8 = 96 cm³

Kết quả cho thấy thể tích của khối chóp tứ giác đều là 96 centimét khối. Việc làm tròn số và đơn vị đo lường cần được thực hiện phù hợp với yêu cầu của bài toán cụ thể.

Dấu hiệu nhận biết và tính chất của khối chóp tứ giác đều

Dấu hiệu nhận biết chóp tứ giác đều là một khối đa diện có đáy là hình vuông và các mặt bên là những tam giác đều bằng nhau. Trong hình học không gian oxyz, khối chóp tứ giác đều là một trường hợp đặc biệt của khối chóp với những tính chất độc đáo.

Để hiểu rõ hơn về khối chóp tứ giác đều, cần phân tích các đặc điểm cơ bản của các thành phần cấu tạo nên khối chóp này. Thể tích khối chóp tứ giác được xác định dựa trên diện tích đáy và chiều cao, tuân theo công thức cơ bản V = (1/3)Sh, trong đó S là diện tích đáy và h là chiều cao.

Các đặc điểm của đáy

Đáy của khối chóp tứ giác đều là một hình vuông hoàn hảo với bốn cạnh bằng nhau và bốn góc vuông. Điều này tạo nên tính đối xứng cao cho toàn bộ khối chóp.

Các đường chéo của đáy vuông góc với nhau và bằng nhau về độ dài. Giao điểm của hai đường chéo đáy chính là hình chiếu vuông góc của đỉnh khối chóp xuống mặt đáy.

Tâm của hình vuông đáy trùng với giao điểm của hai đường chéo và là chân của đường cao khối chóp. Đây là điểm quan trọng để xác định vị trí của đường cao.

Các đặc điểm của mặt bên

Bốn mặt bên của khối chóp tứ giác đều là những tam giác đều hoàn toàn giống nhau. Mỗi tam giác này có ba cạnh bằng nhau và ba góc bằng 60 độ.

Các cạnh bên của khối chóp đều nghiêng một góc alpha so với mặt đáy, và góc này bằng nhau cho tất cả các cạnh bên. Góc giữa hai mặt bên kề nhau cũng bằng nhau.

Đường cao của mỗi mặt bên tam giác đều chia đôi cạnh đáy tương ứng. Điều này tạo nên tính đối xứng hoàn hảo cho toàn bộ khối chóp.

Các đặc điểm của chiều cao

Chiều cao của khối chóp tứ giác đều là đoạn thẳng từ đỉnh vuông góc với mặt đáy. Đường cao này đi qua tâm của hình vuông đáy và tạo thành trục đối xứng của khối chóp.

Khoảng cách từ đỉnh đến bất kỳ điểm nào trên chu vi đáy đều bằng nhau. Đây là một tính chất quan trọng giúp phân biệt khối chóp tứ giác đều với các loại khối chóp khác.

Tỷ lệ giữa chiều cao và cạnh đáy của khối chóp tứ giác đều có mối quan hệ đặc biệt, quyết định độ nghiêng của các mặt bên và góc giữa đường cao với các cạnh bên.

So sánh khối chóp tứ giác đều với các khối chóp khác

So sánh khối chóp tứ giác đều và khối chóp khác giúp hiểu rõ hơn về đặc điểm và tính chất của từng loại hình học. Mỗi loại khối chóp có những đặc trưng riêng về cấu tạo, kích thước và cách tính thể tích. Việc so sánh sẽ giúp phân biệt rõ sự khác biệt giữa chúng.

So với khối chóp tam giác đều

Khối chóp tứ giác đều có đáy là hình vuông, trong khi khối chóp tam giác đều có đáy là tam giác đều. Điều này dẫn đến sự khác biệt về số mặt bên – khối chóp tứ giác đều có 4 mặt bên còn khối chóp tam giác đều chỉ có 3 mặt bên.

Về thể tích chóp tứ giác đều, công thức tính phức tạp hơn so với khối chóp tam giác đều do có thêm một cạnh đáy. Để tính chính xác thể tích, có thể tham khảo cách tính thể tích hình hộp tam giác và áp dụng các nguyên tắc tương tự.

So với khối chóp tứ giác không đều

Khối chóp tứ giác đều có tất cả các cạnh bên bằng nhau và đáy là hình vuông. Ngược lại, khối chóp tứ giác không đều có thể có đáy là hình chữ nhật hoặc hình thang, các cạnh bên không nhất thiết phải bằng nhau.

Điểm đặc biệt của khối chóp tứ giác đều là đường cao luôn vuông góc với mặt đáy và trùng với tâm của hình vuông đáy. Trong khi đó, khối chóp tứ giác không đều có đường cao có thể không vuông góc với mặt đáy.

So với khối chóp ngũ giác đều

Khối chóp ngũ giác đều có 5 mặt bên và đáy là hình ngũ giác đều, nhiều hơn một mặt so với khối chóp tứ giác đều. Điều này tạo nên sự phức tạp hơn trong cấu trúc và cách tính toán.

Mặc dù cả hai đều là khối chóp đều, nhưng khối chóp ngũ giác đều có độ đối xứng cao hơn với 5 trục đối xứng, trong khi khối chóp tứ giác đều chỉ có 4 trục đối xứng. Điều này ảnh hưởng đến tính chất hình học và ứng dụng thực tế của chúng.

Bài tập thực hành tính thể tích khối chóp tứ giác đều

Việc thực hành tính thể tích hình chóp tứ giác qua các bài tập giúp học sinh nắm vững kiến thức và phát triển kỹ năng giải toán không gian. Để nâng cao hiệu quả học tập, Dạy toán trực tuyến cung cấp hệ thống bài tập từ cơ bản đến nâng cao. Các ví dụ bài tập thể tích chóp tứ giác đều được thiết kế phù hợp với trình độ và khả năng tiếp thu của học sinh.

Bài tập cơ bản

Bài tập cơ bản tập trung vào việc áp dụng công thức tính thể tích cơ bản của khối chóp tứ giác đều. Học sinh cần nắm vững cách xác định các yếu tố như diện tích đáy và chiều cao của khối chóp.

Một khối chóp tứ giác đều có cạnh đáy là 6cm và chiều cao 8cm. Việc tính thể tích sẽ được thực hiện theo trình tự: Tính diện tích đáy, sau đó nhân với 1/3 chiều cao để ra kết quả cuối cùng.

Các bài tập này giúp học sinh làm quen với phương pháp giải và rèn luyện kỹ năng tính toán chính xác.

Bài tập nâng cao

Ở cấp độ nâng cao, các bài tập yêu cầu phân tích sâu hơn về mối quan hệ giữa các yếu tố trong khối chóp. Học sinh cần vận dụng kiến thức về tam giác đồng dạng, định lý Pythagoras và các công thức lượng giác.

Một ví dụ điển hình là bài toán tìm thể tích khối chóp khi biết góc giữa mặt bên và mặt đáy. Bài toán này đòi hỏi khả năng phân tích không gian và kỹ năng chuyển đổi giữa các yếu tố hình học.

Bài tập ứng dụng thực tế

Các ứng dụng của khối chóp tứ giác đều xuất hiện trong nhiều lĩnh vực thực tế như kiến trúc và thiết kế. Một ví dụ thực tế là việc tính thể tích của mái nhà hình chóp trong kiến trúc truyền thống Việt Nam.

Trong ngành công nghiệp đóng gói, việc tính thể tích các hộp quà hình chóp giúp tối ưu hóa không gian lưu trữ và vận chuyển. Các công ty như LEGO thường sử dụng tính toán thể tích khối chóp trong thiết kế bao bì sản phẩm.

Bài tập thực tế còn bao gồm việc tính toán lượng vật liệu cần thiết để xây dựng các công trình có hình dạng chóp tứ giác đều, giúp học sinh thấy được giá trị ứng dụng của kiến thức toán học.

Khối chóp tứ giác đều là một trong những hình khối quan trọng trong hình học không gian. Để tính thể tích khối chóp tứ giác đều, bạn cần nắm rõ công thức cũng như các bước thực hiện. Bài viết đã phân tích chi tiết cách tính, đặc điểm, ứng dụng và so sánh với các khối chóp khác, giúp bạn có cái nhìn tổng quan và áp dụng vào bài tập hiệu quả hơn. Hãy khám phá ngay để nâng cao kỹ năng toán học của bạn!