Cách tính diện tích hình ngũ giác và ứng dụng trong toán học thực tiễn

Diện tích hình ngũ giác là một khái niệm quan trọng trong hình học phẳng. Bài viết này sẽ cung cấp đầy đủ công thức, phương pháp và ví dụ để bạn hiểu rõ về cách tính diện tích ngũ giác đều và không đều. Ứng dụng này trong thế giới thực tế và tư duy toán học sẽ giúp bạn có cái nhìn toàn diện hơn về hình học.

Diện tích hình ngũ giác và các khái niệm cơ bản trong hình học phẳng

Trong lý thuyết hình học phẳng, diện tích hình ngũ giác là một trong những khái niệm quan trọng cần nắm vững. Việc tính diện tích của hình ngũ giác thường được thực hiện bằng cách chia nhỏ thành các hình tam giác cơ bản.

Hình ngũ giác là gì ảnh hưởng trực tiếp đến cách tính diện tích của nó. Đối với ngũ giác lồi, diện tích được tính bằng tổng diện tích của 3 tam giác tạo thành khi vẽ 2 đường chéo từ một đỉnh đến các đỉnh không liền kề. Phương pháp này giúp đơn giản hóa việc tính toán và áp dụng các công thức diện tích tam giác cơ bản.

Ngoài ra, với những hình ngũ giác đều, diện tích có thể được tính thông qua công thức đặc biệt liên quan đến độ dài cạnh và bán kính đường tròn ngoại tiếp. Điều này cho phép tính toán nhanh chóng và chính xác hơn so với phương pháp chia nhỏ thành các tam giác thành phần.

Công thức tính diện tích hình ngũ giác đều và không đều

Công thức tính diện tích hình ngũ giác là một trong những kiến thức quan trọng trong hình học. Tùy thuộc vào đặc điểm của ngũ giác mà có thể áp dụng các phương pháp tính khác nhau. Với ngũ giác đều, việc tính diện tích khá đơn giản nhờ tính đối xứng. Ngược lại, ngũ giác không đều đòi hỏi phải chia nhỏ thành các hình cơ bản hoặc sử dụng tọa độ các đỉnh.

Công thức tính diện tích ngũ giác đều

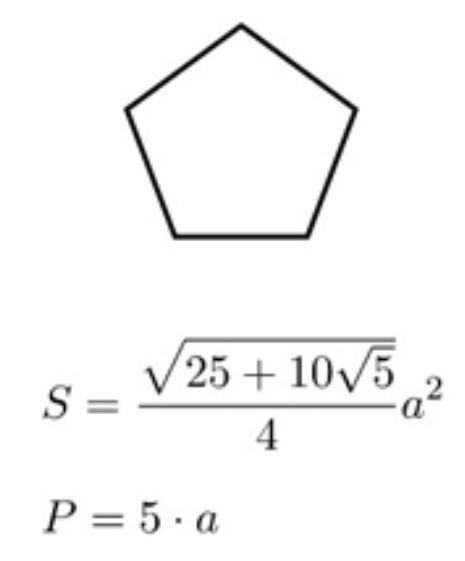
Diện tích ngũ giác đều được tính bằng công thức: S = (5 × a² × cot 36°)/4, trong đó a là độ dài cạnh. Công thức này dựa trên nguyên lý chia ngũ giác đều thành 5 tam giác đều từ tâm. Mỗi tam giác có diện tích bằng (a² × cot 36°)/4, tổng 5 tam giác cho ra diện tích ngũ giác đều.

Một cách tính khác là sử dụng bán kính đường tròn ngoại tiếp R: S = (5 × R² × sin 72°)/2. Phương pháp này thường được áp dụng khi biết bán kính đường tròn ngoại tiếp thay vì độ dài cạnh.

Phương pháp chia nhỏ để tính diện tích ngũ giác không đều

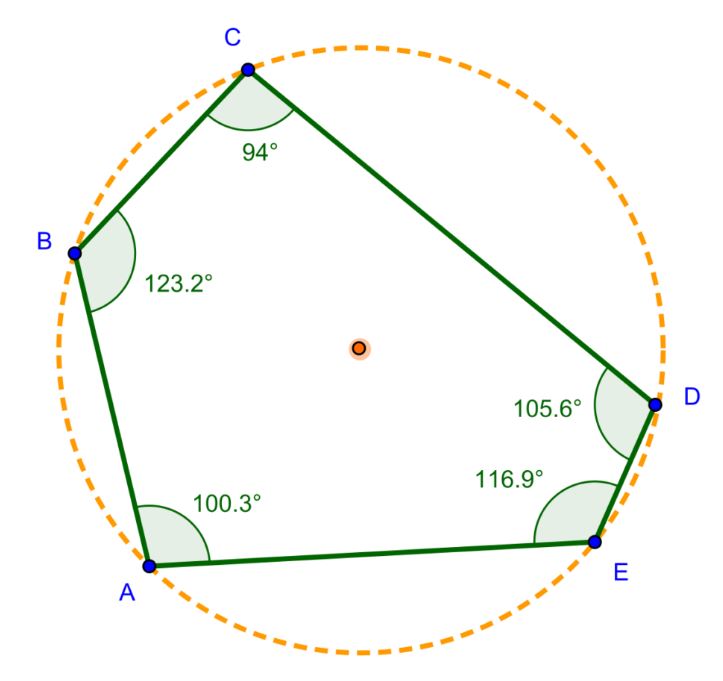
Cách tính diện tích hình ngũ giác không đều phổ biến nhất là chia thành các tam giác. Bằng cách vẽ các đường chéo từ một đỉnh đến các đỉnh không liền kề, ngũ giác được chia thành 3 tam giác. Diện tích ngũ giác bằng tổng diện tích các tam giác thành phần.

Phương pháp này đặc biệt hiệu quả khi có thể đo được độ dài các cạnh và đường chéo. Việc tính diện tích từng tam giác có thể sử dụng công thức Heron hoặc công thức sin nếu biết các góc.

Công thức tính diện tích ngũ giác bằng tọa độ các đỉnh

Khi biết tọa độ các đỉnh (x₁,y₁), (x₂,y₂), (x₃,y₃), (x₄,y₄), (x₅,y₅), diện tích ngũ giác được tính bằng công thức: S = 1/2|x₁y₂ + x₂y₃ + x₃y₄ + x₄y₅ + x₅y₁ – y₁x₂ – y₂x₃ – y₃x₄ – y₄x₅ – y₅x₁|. Đây là mở rộng của Diện tích hình đa giác áp dụng cho trường hợp 5 đỉnh.

Phương pháp này đặc biệt hữu ích trong các ứng dụng máy tính và đồ họa, nơi các điểm thường được biểu diễn bằng tọa độ. Công thức có thể áp dụng cho mọi ngũ giác, không phụ thuộc vào hình dạng đều hay không đều.

Các phương pháp giải bài tập về diện tích hình ngũ giác

Việc tính diện tích hình ngũ giác đòi hỏi sự linh hoạt trong việc áp dụng các phương pháp khác nhau tùy thuộc vào đặc điểm của từng bài toán. Mỗi phương pháp có những ưu điểm và hạn chế riêng, người giải cần nắm vững để lựa chọn cách tiếp cận phù hợp nhất.

Phương pháp chia thành các hình cơ bản

Phương pháp này dựa trên nguyên tắc phân tách ngũ giác thành các hình tam giác hoặc tứ giác đơn giản hơn. Bằng cách vẽ các đường chéo từ một đỉnh đến các đỉnh không liền kề, ta có thể chia ngũ giác thành 3 tam giác.

Sau khi chia nhỏ, ta có thể áp dụng diện tích tam giác trong oxyz hoặc các công thức tính diện tích tam giác cơ bản để tính từng phần. Tổng diện tích các hình nhỏ sẽ cho ta kết quả cuối cùng.

Phương pháp sử dụng công thức trực tiếp

Đối với ngũ giác đều, ta có thể áp dụng công thức S = (5a²/4) × cotg(36°), trong đó a là độ dài cạnh. Phương pháp này đặc biệt hiệu quả khi xử lý các ngũ giác đều hoặc ngũ giác có tính đối xứng cao.

Ngoài ra, với ngũ giác lồi bất kỳ, ta có thể sử dụng công thức dựa trên tọa độ các đỉnh: S = 1/2|x₁y₂ + x₂y₃ + x₃y₄ + x₄y₅ + x₅y₁ – y₁x₂ – y₂x₃ – y₃x₄ – y₄x₅ – y₅x₁|. Phương pháp này đặc biệt hữu ích khi làm việc với hệ tọa độ.

Phương pháp sử dụng tính chất đặc biệt

Khi ngũ giác có các tính chất đặc biệt như đối xứng, ta có thể tận dụng để đơn giản hóa quá trình tính toán. Ví dụ với ngũ giác có tâm đối xứng, ta có thể chia thành 5 tam giác bằng nhau từ tâm.

Một số ngũ giác có thể được xem như sự kết hợp của các hình quen thuộc như hình chữ nhật và tam giác. Trong trường hợp này, việc nhận diện và tách các thành phần sẽ giúp cách tính diện tích ngũ giác trở nên đơn giản và hiệu quả hơn.

Ví dụ minh họa và bài tập về tính diện tích hình ngũ giác

Để giúp người học nắm vững cách tính diện tích hình ngũ giác, việc thực hành qua các ví dụ về diện tích ngũ giác cụ thể là rất quan trọng. Các bài tập được thiết kế từ cơ bản đến nâng cao, giúp rèn luyện kỹ năng tính toán và áp dụng công thức một cách linh hoạt.

Trong quá trình giải các bài tập diện tích ngũ giác, người học cần nắm vững phương pháp chia nhỏ hình ngũ giác thành các hình cơ bản như tam giác, hình thoi hoặc hình viên phân. Điều này giúp việc tính toán trở nên đơn giản và chính xác hơn.

Bài tập tính diện tích ngũ giác đều

Bài tập 1: Cho ngũ giác đều cạnh 6cm, đường cao h = 4,5cm. Tính diện tích ngũ giác.
Lời giải: Diện tích = (5 × 6 × 4,5)/2 = 67,5 cm²

Bài tập 2: Tính diện tích ngũ giác đều có cạnh 8cm và bán kính đường tròn ngoại tiếp R = 7cm.
Lời giải: Diện tích = (5 × 8² × sin72°)/4 = 120,7 cm²

Bài tập tính diện tích ngũ giác không đều

Bài tập 3: Cho ngũ giác ABCDE được chia thành 3 tam giác: ABC (20cm²), CDE (15cm²), ACE (25cm²). Tính diện tích ngũ giác.
Lời giải: Diện tích = 20 + 15 + 25 = 60 cm²

Bài tập 4: Ngũ giác MNPQR có đường chéo MQ và NQ chia thành 3 tam giác: MNQ (12cm²), NPQ (18cm²), QRM (15cm²). Tính diện tích ngũ giác.
Lời giải: Diện tích = 12 + 18 + 15 = 45 cm²

Bài tập tổng hợp

Bài tập 5: Ngũ giác ABCDE có diện tích 100cm². Điểm O nằm trong ngũ giác tạo với các đỉnh thành 5 tam giác bằng nhau. Tính diện tích mỗi tam giác.
Lời giải: Diện tích mỗi tam giác = 100/5 = 20 cm²

Bài tập 6: Cho ngũ giác KLMNP có diện tích 80cm². Đường chéo KM và KN chia ngũ giác thành 3 phần có tỷ lệ 2:3:3. Tính diện tích từng phần.
Lời giải:

• Phần thứ nhất: 80 × 2/8 = 20 cm²
• Phần thứ hai: 80 × 3/8 = 30 cm²
• Phần thứ ba: 80 × 3/8 = 30 cm²

Ứng dụng thực tế của diện tích hình ngũ giác trong đời sống và kiến trúc

Diện tích hình ngũ giác có nhiều ứng dụng quan trọng trong thực tế, từ thiết kế kiến trúc đến đo đạc địa chính. Việc tính toán chính xác diện tích giúp tối ưu hóa không gian và tiết kiệm chi phí trong xây dựng. Các công trình có mặt bằng ngũ giác thường mang tính thẩm mỹ cao và tạo điểm nhấn độc đáo cho cảnh quan.

Trong quy hoạch đô thị, hình ngũ giác được ứng dụng để thiết kế các quảng trường, công viên hay khu vui chơi. Điều này tạo nên sự đa dạng về hình khối, tránh sự đơn điệu của các hình chữ nhật thông thường. Nhiều công trình nổi tiếng thế giới như Lầu Năm Góc (Pentagon) tại Mỹ là minh chứng cho sự kết hợp hoàn hảo giữa công năng và thẩm mỹ của hình ngũ giác.

Ứng dụng trong thiết kế và xây dựng

Trong lĩnh vực kiến trúc, việc tính toán diện tích ngũ giác đóng vai trò then chốt khi thiết kế các công trình đặc biệt. Kiến trúc sư thường kết hợp hình ngũ giác với các hình khối khác như thể tích hình hộp tam giác để tạo nên những không gian độc đáo.

Các trung tâm thương mại hiện đại thường sử dụng mặt bằng ngũ giác để tối ưu hóa lưu thông và tầm nhìn. Theo nghiên cứu của Viện Kiến trúc Quốc gia, thiết kế ngũ giác giúp tăng hiệu quả sử dụng không gian lên đến 15% so với các hình dạng thông thường.

Xu hướng thiết kế bền vững cũng ưa chuộng hình ngũ giác khi kết hợp với diện tích hình lục giác để tạo nên các mô-đun năng lượng mặt trời hiệu quả. Điều này không chỉ tối ưu về mặt kỹ thuật mà còn mang lại giá trị thẩm mỹ cao.

Ứng dụng trong đo đạc thực tế

Trong công tác đo đạc địa chính, việc xác định diện tích các thửa đất hình ngũ giác đòi hỏi độ chính xác cao. Các kỹ sư trắc địa sử dụng công nghệ GPS và phần mềm chuyên dụng để đo đạc các góc và cạnh một cách chính xác.

Ngành nông nghiệp ứng dụng phương pháp đo đạc ngũ giác trong quy hoạch các khu canh tác. Theo số liệu từ Cục Đo đạc và Bản đồ Việt Nam, phương pháp này giúp tận dụng tối đa diện tích đất nông nghiệp, đặc biệt ở các khu vực đồi núi có địa hình phức tạp.

Các ứng dụng diện tích ngũ giác còn được thể hiện trong việc thiết kế hệ thống tưới tiêu. Các khu vực canh tác hình ngũ giác cho phép bố trí hệ thống phun nước hiệu quả, tiết kiệm nguồn nước và năng lượng vận hành.

Khi tìm hiểu về diện tích hình ngũ giác, bạn sẽ khám phá nhiều công thức và phương pháp khác nhau, từ cách tính diện tích ngũ giác đều đến những hình không đều. Việc nắm rõ các kiến thức này không chỉ giúp bạn vượt qua các bài tập mà còn ứng dụng hiệu quả trong thực tế. Hãy áp dụng những kiến thức này vào việc giải bài tập để trở nên tự tin hơn trong môn hình học nhé!