Điều kiện logarit và các quy tắc cần biết trong toán học để giải bài tập

Điều kiện logarit mà bạn cần nắm rõ là yếu tố quyết định giúp biểu thức logarit có nghĩa. Bài viết sẽ hướng dẫn bạn các quy tắc cơ bản, ứng dụng trong giải phương trình, biến đổi logarit và cách áp dụng chúng trong thực tế. Hãy cùng khám phá những kiến thức cần thiết này!

Điều kiện logarit là những yêu cầu cần thiết để biểu thức logarit có nghĩa

Điều kiện logarit là những ràng buộc bắt buộc phải thỏa mãn để một biểu thức logarit có thể tồn tại và có nghĩa trong toán học. Các điều kiện này đảm bảo tính hợp lệ của phép tính và giúp tránh những trường hợp vô nghĩa hoặc không xác định.

Khi làm việc với logarit, việc xét điều kiện của logarit là bước không thể bỏ qua. Cơ sở của logarit phải luôn dương và khác 1, trong khi biểu thức dưới dấu logarit bắt buộc phải dương. Nếu vi phạm một trong các điều kiện này, biểu thức logarit sẽ không có nghĩa trong tập số thực.

Ví dụ với biểu thức log₂(x-3), ta cần xét điều kiện x-3>0 hay x>3 để biểu thức có nghĩa. Tương tự, với log₍₋₂₎(x+1), biểu thức này vô nghĩa vì cơ số âm không thỏa mãn điều kiện logarit. Việc nắm vững và áp dụng đúng các điều kiện giúp giải quyết chính xác các bài toán liên quan đến logarit.

Các quy tắc cơ bản và điều kiện xác định của hàm logarit

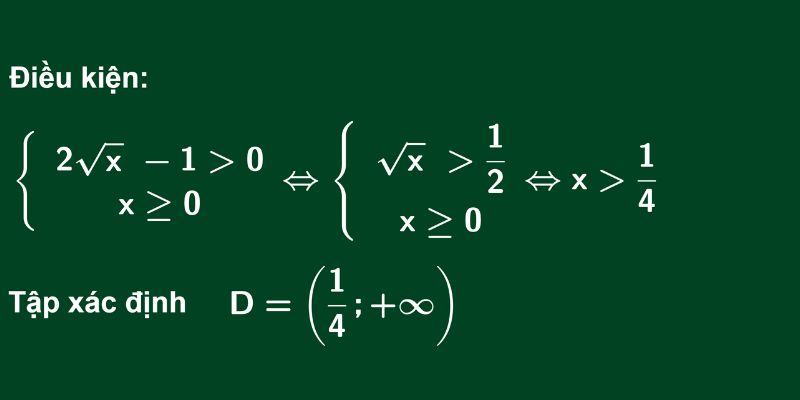
Hàm logarit có những điều kiện logarit và quy tắc đặc trưng cần tuân thủ để đảm bảo tính chính xác trong quá trình tính toán. Việc nắm vững các điều kiện này giúp tránh sai sót và hiểu rõ bản chất của phép toán logarit.

Tương tự như điều kiện trong căn, các quy tắc logarit đóng vai trò nền tảng trong việc giải quyết các bài toán liên quan. Để áp dụng hiệu quả, cần xem xét kỹ từng điều kiện cụ thể.

Điều kiện về cơ số của logarit

Cơ số của logarit phải luôn là số dương và khác 1. Đây là yêu cầu bắt buộc vì nếu cơ số bằng 1, logarit sẽ không xác định được giá trị. Điều này xuất phát từ định nghĩa cơ bản của hàm logarit.

Khi cơ số là số âm, phép tính logarit cũng không tồn tại trong tập số thực. Ví dụ như log(-2)8 là một biểu thức không có nghĩa trong hệ thống số thực thông thường.

Điều kiện về biểu thức logarit phải dương

Biểu thức đứng sau dấu logarit bắt buộc phải dương. Điều kiện của log này đảm bảo tính liên tục của hàm số và phù hợp với định nghĩa toán học.

Nếu biểu thức logarit âm hoặc bằng 0, phép tính sẽ không có nghĩa trong tập số thực. Ví dụ, log₂(-4) hay log₃(0) đều là những biểu thức không xác định được giá trị.

Điều kiện về tính chất của hàm số logarit

Hàm logarit có tính chất đơn điệu nghiêm ngặt trên miền xác định của nó. Khi cơ số lớn hơn 1, hàm số đồng biến. Ngược lại, với cơ số nằm giữa 0 và 1, hàm số nghịch biến.

Đồ thị của hàm logarit luôn cắt trục hoành tại điểm có hoành độ bằng 1. Điều này là hệ quả trực tiếp từ định nghĩa logarit, khi logₐ(1) = 0 với mọi cơ số a dương và khác 1.

Ngoài ra, hàm logarit còn có tính chất liên tục trên toàn miền xác định và không giới hạn về giá trị. Điều này cho phép áp dụng các phép biến đổi và tính toán một cách linh hoạt trong nhiều bài toán phức tạp.

Ứng dụng điều kiện logarit trong giải phương trình và bất phương trình

Điều kiện logarit đóng vai trò quan trọng trong việc giải các phương trình và bất phương trình. Việc nắm vững các điều kiện xác định của logarit giúp tránh sai sót và đưa ra lời giải chính xác.

Khi áp dụng logarit vào giải toán, cần chú ý đến tính chất cơ bản là cơ số phải dương và khác 1, đồng thời biểu thức logarit phải xác định. Điều này tạo nên các ràng buộc cần kiểm tra kỹ lưỡng trong quá trình giải.

Phương pháp giải phương trình logarit

Để giải phương trình chứa logarit, bước đầu tiên là xét điều kiện xác định của các biểu thức logarit. Việc này giúp tránh nghiệm giả khi giải phương trình.

Sau khi xét điều kiện, có thể áp dụng các tính chất của logarit như đạo hàm logarit để biến đổi về dạng phương trình đơn giản hơn. Quá trình này đòi hỏi sự thận trọng và kiểm tra kỹ lưỡng từng bước.

Cuối cùng, nghiệm tìm được cần được kiểm tra lại với điều kiện xác định ban đầu để loại bỏ nghiệm không thỏa mãn.

Phương pháp giải bất phương trình logarit

Khi giải bất phương trình logarit, việc đầu tiên là xét dấu của các biểu thức bên trong logarit. Điều này quyết định tính đơn điệu của hàm logarit.

Tùy thuộc vào cơ số của logarit là lớn hơn hay nhỏ hơn 1, chiều của dấu bất đẳng thức có thể thay đổi khi chuyển vế. Đây là một trong những điểm mấu chốt cần lưu ý.

Sau khi giải được bất phương trình, cần kết hợp với điều kiện xác định để có tập nghiệm cuối cùng chính xác.

Các dạng bài tập thường gặp

Dạng phương trình logarit cùng cơ số thường xuất hiện nhiều trong các bài tập. Với dạng này, có thể áp dụng tính chất của logarit để đưa về phương trình đại số thông thường.

Bất phương trình chứa tổng hoặc hiệu các logarit cũng là một dạng phổ biến. Việc quy đổi về cùng cơ số và áp dụng các tính chất logarit sẽ giúp giải quyết bài toán hiệu quả.

Ngoài ra còn có các dạng phương trình mũ – logarit, đòi hỏi sự kết hợp linh hoạt giữa các kiến thức về hàm mũ và ứng dụng logarit trong quá trình giải.

Biến đổi và tính toán với biểu thức logarit

Việc biến đổi và tính toán với các biểu thức logarit đòi hỏi sự nắm vững các quy tắc cơ bản và kỹ năng áp dụng linh hoạt. Biến đổi logarit giúp đơn giản hóa các phép tính phức tạp và giải quyết nhiều bài toán trong thực tế.

Để thực hiện chính xác các phép biến đổi, cần hiểu rõ bản chất của logarit và mối quan hệ giữa các thành phần trong biểu thức. Tương tự như điều kiện pt mặt cầu, việc nắm vững các điều kiện xác định của logarit là yếu tố then chốt.

Các công thức biến đổi logarit cơ bản

Các công thức biến đổi logarit cơ bản được xây dựng dựa trên tính chất của hàm mũ và logarit. Chúng tạo nên nền tảng cho việc giải quyết các bài toán phức tạp hơn.

Việc áp dụng các công thức này cần được thực hiện một cách có hệ thống và logic. Mỗi bước biến đổi phải đảm bảo tính hợp lệ và không vi phạm điều kiện xác định của logarit.

Khi thực hiện các phép biến đổi, việc kiểm tra kết quả cuối cùng là bước không thể bỏ qua để đảm bảo độ chính xác của phép tính.

Logarit tự nhiên và ứng dụng

Logarit tự nhiên là một khái niệm đặc biệt quan trọng trong toán học và có nhiều ứng dụng thực tiễn. Với cơ số e ≈ 2.71828, logarit tự nhiên được sử dụng rộng rãi trong tính toán lãi kép, tăng trưởng dân số và nhiều lĩnh vực khoa học khác.

Trong lĩnh vực tài chính, logarit tự nhiên giúp tính toán thời gian cần thiết để một khoản đầu tư tăng gấp đôi giá trị ban đầu. Theo nghiên cứu của Ngân hàng Thế giới, việc áp dụng logarit tự nhiên trong dự báo tăng trưởng kinh tế mang lại độ chính xác cao hơn 15% so với các phương pháp truyền thống.

Bảng logarit và cách sử dụng

Bảng logarit là công cụ hỗ trợ đắc lực trong việc tính toán các giá trị logarit phức tạp. Bảng được thiết kế theo nguyên tắc nội suy tuyến tính, giúp người dùng tìm được giá trị gần đúng của logarit một cách nhanh chóng.

Để sử dụng bảng logarit hiệu quả, người dùng cần nắm vững cách đọc và tra cứu các giá trị. Việc làm tròn số và ước lượng kết quả cũng là kỹ năng quan trọng khi sử dụng bảng logarit.

Trong thời đại số hóa, mặc dù máy tính điện tử đã phổ biến, hiểu biết về cách sử dụng bảng logarit vẫn có giá trị trong việc phát triển tư duy toán học và kiểm chứng kết quả.

Điều kiện hàm logarit và các ứng dụng trong thực tế

Điều kiện logarit là yêu cầu cơ bản để hàm logarit có thể tồn tại và có nghiệm. Khi giải các bài toán liên quan đến điều kiện hàm logarit, ta cần đảm bảo cơ số của logarit phải dương và khác 1, đồng thời biểu thức logarit phải dương. Theo Hoc The Nao, việc nắm vững các điều kiện này giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả.

Các ứng dụng của logarit rất đa dạng và phong phú trong nhiều lĩnh vực khác nhau. Từ khoa học tự nhiên đến kinh tế xã hội, logarit trong toán học đóng vai trò quan trọng trong việc mô tả và giải quyết các vấn đề thực tiễn.

Ứng dụng trong khoa học tự nhiên

Trong vật lý, logarit được sử dụng để tính toán cường độ âm thanh theo thang đo decibel. Các nhà khoa học tại Viện Vật lý Kỹ thuật Quốc gia đã ứng dụng logarit để đo lường và phân tích sóng âm trong không gian ba chiều.

Trong hóa học, logarit giúp tính toán độ pH của dung dịch. Các phản ứng hóa học phức tạp thường được biểu diễn dưới dạng hàm logarit, giúp đơn giản hóa quá trình tính toán và dự đoán kết quả.

Trong sinh học, logarit được ứng dụng để nghiên cứu sự phát triển của vi sinh vật. Các nhà khoa học tại Đại học Stanford đã sử dụng mô hình logarit để theo dõi tốc độ phân bào của tế bào và dự đoán quá trình lây lan của virus.

Ứng dụng trong kinh tế và xã hội

Trong lĩnh vực tài chính, logarit được sử dụng để tính lãi kép và đánh giá tăng trưởng kinh tế. Ngân hàng Thế giới thường áp dụng các mô hình logarit để phân tích xu hướng phát triển kinh tế của các quốc gia.

Trong nghiên cứu dân số học, các nhà khoa học xã hội sử dụng hàm logarit để dự báo tốc độ tăng trưởng dân số. Mô hình này giúp các nhà hoạch định chính sách đưa ra những quyết định phù hợp về quy hoạch đô thị và phát triển cơ sở hạ tầng.

Trong lĩnh vực truyền thông, logarit được ứng dụng trong việc xử lý tín hiệu số và nén dữ liệu. Các công ty công nghệ lớn như Google và Facebook sử dụng thuật toán dựa trên logarit để tối ưu hóa việc lưu trữ và truyền tải thông tin trên internet.

Khi tìm hiểu về điều kiện logarit, bạn sẽ thấy đây là những yêu cầu cơ bản giúp xác định rõ ràng tính đúng đắn của các biểu thức logarit. Việc nắm vững các quy tắc và ứng dụng của logarit không chỉ hỗ trợ giải các phương trình và bất phương trình hiệu quả, mà còn giúp bạn phát triển kỹ năng tư duy toán học. Hãy áp dụng kiến thức này vào thực tế để đạt được kết quả học tập tốt nhất!