Tìm hiểu giá trị cực đại là y hay x trong hàm số và cách áp dụng

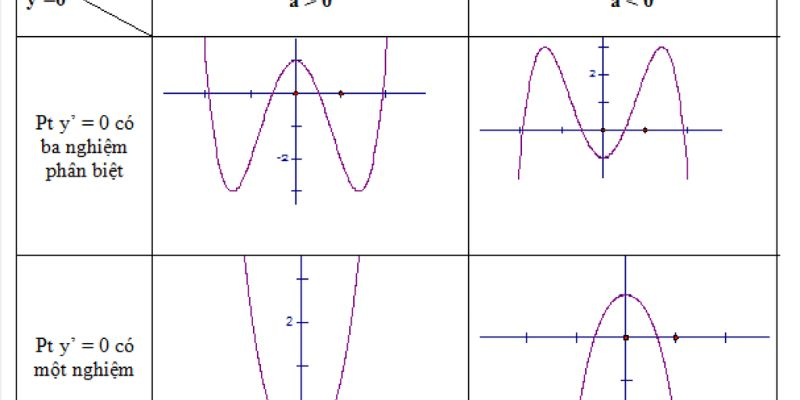
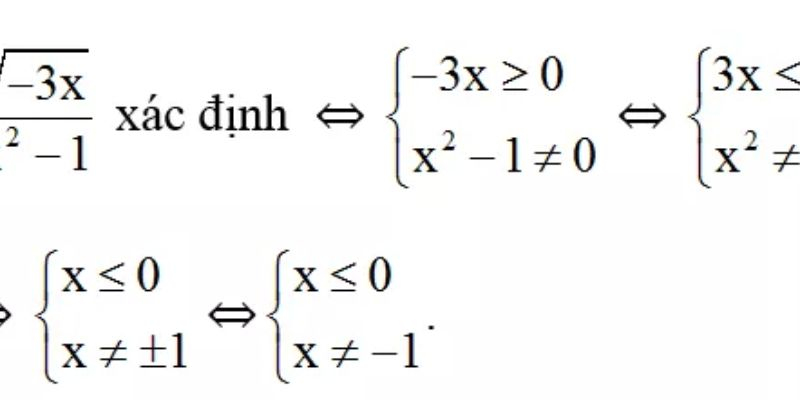Giá trị cực đại là y hay x? Đây là câu hỏi thú vị trong toán học liên quan đến cực trị của hàm số. Bài viết provided hướng dẫn cụ thể về cách xác định giá trị cực đại, cũng như áp dụng các phương pháp tìm giá trị cực tiểu. Với các ví dụ minh họa rõ ràng, bạn sẽ hiểu hơn về cách hoạt động của những khái niệm này trong bài toán thực tế.

Giá trị cực đại là y hay x?

Trong toán học, giá trị cực đại là y hay x phụ thuộc vào cách biểu diễn hàm số và vai trò của các biến. Thông thường, y là giá trị cực đại khi xét hàm số y = f(x), với y là biến phụ thuộc và x là biến độc lập. cực trị là gì

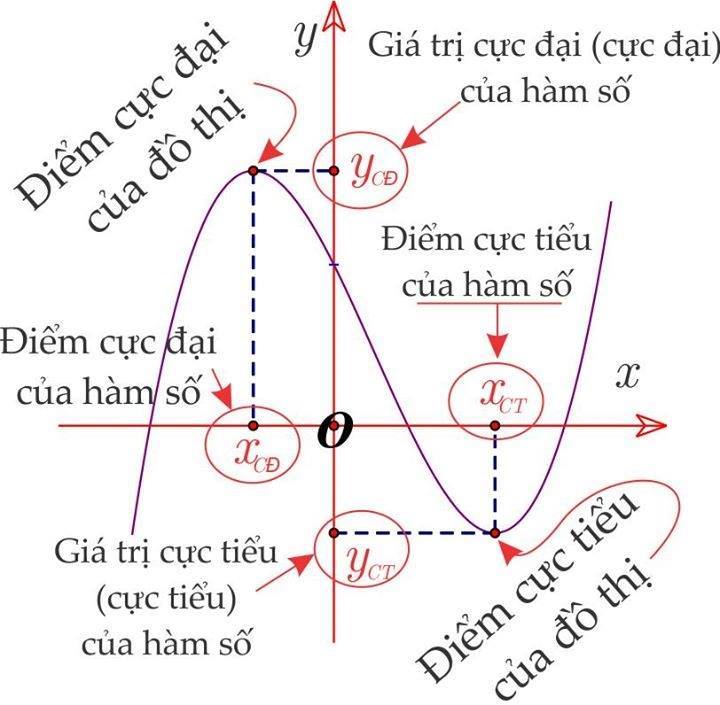
Khi xét một hàm số y = f(x), giá trị y tại điểm cực đại sẽ lớn hơn các giá trị y lân cận. Điều này có nghĩa tại điểm đó, đồ thị hàm số đạt đến đỉnh cao nhất so với các điểm xung quanh. Giá trị x tương ứng được gọi là hoành độ của điểm cực đại.

Ví dụ với hàm số y = -x² + 4, giá trị cực đại của hàm số là y = 4 tại x = 0. Trong trường hợp này, y = 4 chính là giá trị cực đại, còn x = 0 là hoành độ của điểm cực đại. Điều này minh họa rõ ràng rằng giá trị cực đại thuộc về biến phụ thuộc y.

Phương pháp xác định giá trị cực đại và cực tiểu của hàm số

Trong giải tích, việc tìm cực đại và cực tiểu của hàm số đóng vai trò quan trọng để xác định các giá trị tối ưu. Phương pháp này giúp giải quyết nhiều bài toán thực tế như tối ưu hóa chi phí sản xuất hay tìm diện tích lớn nhất.

Để áp dụng phương pháp tìm cực đại hiệu quả, cần nắm vững các khái niệm về đạo hàm và các điểm tới hạn của hàm số. Việc xác định chính xác các điểm này sẽ giúp tìm ra được giá trị cực trị một cách chính xác và nhanh chóng.

Điều kiện để tìm cực trị của hàm số

Điều kiện cần để một điểm là cực trị của hàm số là đạo hàm tại điểm đó bằng 0 hoặc không tồn tại. Tuy nhiên, điều kiện này chưa đủ để kết luận điểm đó là cực trị.

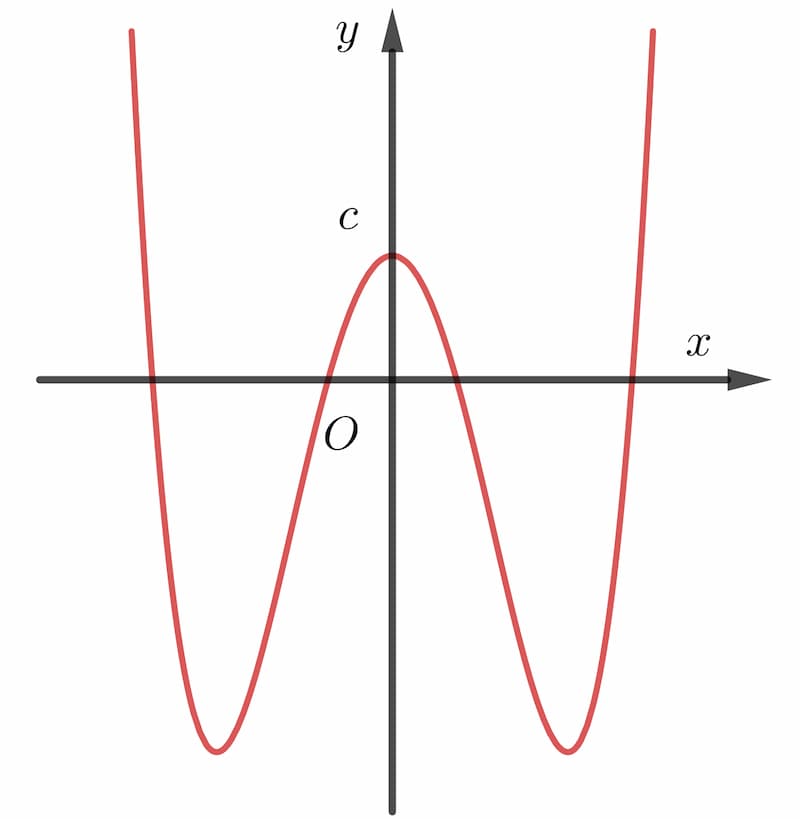
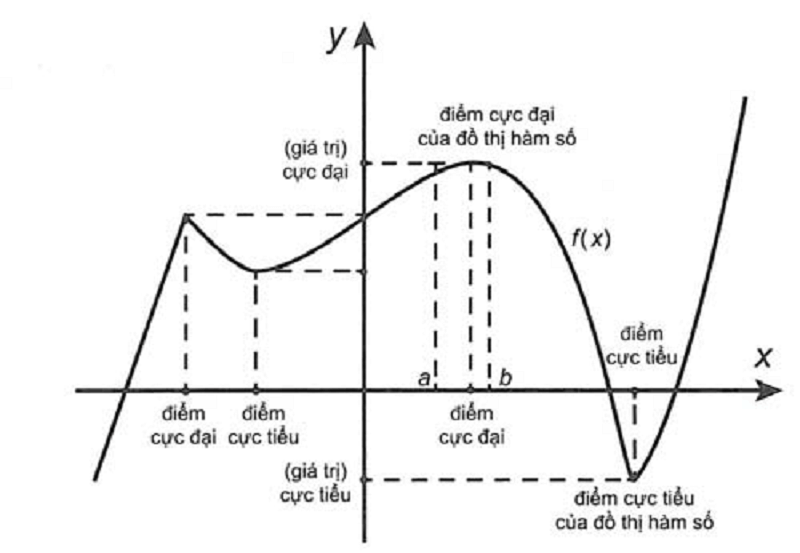
Một điểm được gọi là cực đại khi giá trị hàm số tại điểm đó lớn hơn các giá trị lân cận. Ngược lại, điểm cực tiểu là điểm có giá trị hàm số nhỏ hơn các giá trị xung quanh.

Việc kiểm tra bản chất của điểm tới hạn cần được thực hiện thông qua việc xét dấu đạo hàm hoặc đạo hàm cấp cao hơn. Điều này giúp phân biệt chính xác điểm cực đại hay cực tiểu.

Các bước tìm giá trị cực đại và cực tiểu

Để tìm cực trị của hàm số, cần thực hiện tuần tự các bước sau:

• Xác định miền xác định của hàm số
• Tìm đạo hàm của hàm số
• Tìm các điểm tới hạn
• Kiểm tra bản chất của từng điểm tới hạn

Việc thực hiện đầy đủ và chính xác các bước này sẽ giúp xác định được tất cả các điểm cực trị của hàm số.

Xét dấu đạo hàm

Phương pháp xét dấu đạo hàm giúp xác định chính xác bản chất của điểm tới hạn. Khi đạo hàm đổi dấu từ dương sang âm qua điểm tới hạn, điểm đó là cực đại.

Ngược lại, nếu đạo hàm đổi dấu từ âm sang dương, điểm tới hạn đó là cực tiểu. Trường hợp đạo hàm không đổi dấu, điểm tới hạn không phải là cực trị của hàm số.

Kiểm tra điểm tới hạn

Sau khi tìm được các điểm tới hạn, việc kiểm tra có thể thực hiện qua đạo hàm cấp hai. Nếu đạo hàm cấp hai dương tại điểm tới hạn, điểm đó là cực tiểu.

Trường hợp đạo hàm cấp hai âm tại điểm tới hạn, điểm đó là cực đại. Nếu đạo hàm cấp hai bằng 0, cần kiểm tra thêm đạo hàm cấp cao hơn để kết luận.

Phương pháp này đặc biệt hữu ích khi việc xét dấu đạo hàm gặp khó khăn hoặc phức tạp.

Cách xác định giá trị cực đại của hàm số bậc hai

Để xác định hàm số bậc hai cực đại, cần phân tích đồ thị parabol và áp dụng công thức tính giá trị cực đại. Đồ thị hàm số bậc hai có dạng parabol hướng lên hoặc xuống, tùy thuộc vào hệ số a của hàm số. Khi a < 0, parabol úp và có giá trị cực đại tại đỉnh của đồ thị.

Việc tìm giá trị cực đại không chỉ giúp giải quyết các bài toán toán học thuần túy mà còn có ứng dụng thực tiễn trong nhiều lĩnh vực như kinh tế, kỹ thuật và tối ưu hóa. Ví dụ trong kinh doanh, việc xác định mức giá tối ưu để đạt lợi nhuận cao nhất chính là bài toán tìm cực đại của hàm số bậc hai.

Công thức tính giá trị cực đại hàm bậc hai

Với hàm số bậc hai f(x) = ax² + bx + c (a < 0), giá trị cực đại được xác định qua hai bước chính. Đầu tiên, tìm hoành độ đỉnh của parabol theo công thức x = -b/(2a). Sau đó, thay giá trị x vừa tìm được vào biểu thức của hàm số để tính giá trị cực đại.

Giá trị cực đại của hàm số bậc hai cũng có thể được tính trực tiếp thông qua công thức y = -Δ/(4a) + c, trong đó Δ = b² – 4ac là định thức của hàm số. Công thức này đặc biệt hữu ích khi cần tìm nhanh giá trị cực đại mà không quan tâm đến hoành độ đỉnh.

Phân tích đồ thị parabol

Đồ thị hàm số cực đại có dạng parabol úp xuống khi hệ số a âm. Trục đối xứng của parabol là đường thẳng song song với trục Oy và đi qua đỉnh của đồ thị. Điểm đỉnh chính là điểm có tung độ lớn nhất trên đồ thị, tương ứng với giá trị cực đại của hàm số.

Khi phân tích đồ thị, cần chú ý đến sự thay đổi của các hệ số a, b và c. Hệ số a quyết định độ mở của parabol, hệ số b ảnh hưởng đến vị trí của trục đối xứng, và hệ số c xác định điểm cắt của đồ thị với trục Oy.

Ví dụ minh họa tìm cực đại hàm bậc hai

Xét hàm số f(x) = -2x² + 4x + 5. Đây là hàm bậc hai có hệ số a = -2 < 0 nên đồ thị là parabol úp và có giá trị cực đại. Áp dụng công thức tìm hoành độ đỉnh: x = -4/(-4) = 1.

Thay x = 1 vào biểu thức ban đầu:
f(1) = -2(1)² + 4(1) + 5 = -2 + 4 + 5 = 7

Vậy giá trị cực đại của hàm số là 7, đạt được tại x = 1. Kết quả có thể kiểm chứng bằng cách vẽ đồ thị hoặc thử các giá trị x khác, sẽ thấy f(x) luôn nhỏ hơn hoặc bằng 7.

Ứng dụng giá trị cực đại trong giải toán thực tế

Việc tìm giá trị cực đại là y hay x phụ thuộc vào bài toán cụ thể và mục tiêu cần tối ưu. Các ứng dụng giá trị cực đại xuất hiện trong nhiều lĩnh vực từ hình học, kinh tế đến các bài toán thực tiễn. Theo Học Thế Nào, việc nắm vững phương pháp tìm cực trị giúp giải quyết hiệu quả nhiều vấn đề tối ưu trong cuộc sống.

Bài toán tối ưu trong hình học

Trong hình học, việc tìm giá trị cực đại thường liên quan đến diện tích, thể tích hoặc chu vi của các hình. Ví dụ như tìm hình chữ nhật có chu vi cho trước sao cho diện tích đạt lớn nhất, hay tìm hình hộp chữ nhật có thể tích lớn nhất với diện tích xung quanh cho trước.

Một ứng dụng điển hình là bài toán thiết kế bao bì sản phẩm. Công ty Tetra Pak đã áp dụng nguyên lý tối ưu hóa để thiết kế hộp sữa hình lăng trụ có thể tích tối đa trong khi tiết kiệm vật liệu đóng gói.

Bài toán kinh tế về lợi nhuận cực đại

Trong kinh doanh, việc tối đa hóa lợi nhuận là mục tiêu quan trọng của mọi doanh nghiệp. Điều này đòi hỏi phân tích mối quan hệ giữa doanh thu và chi phí để tìm điểm cân bằng tối ưu.

Các yếu tố cần xem xét khi tối ưu hóa lợi nhuận:

• Chi phí cố định và chi phí biến đổi
• Giá bán sản phẩm và số lượng tiêu thụ
• Điểm hòa vốn và ngưỡng sinh lời

Việc xác định chính xác các yếu tố trên giúp doanh nghiệp đưa ra quyết định sản xuất kinh doanh hiệu quả.

Bài toán về khoảng cách

Bài toán tìm khoảng cách ngắn nhất hoặc dài nhất giữa hai điểm, đường thẳng hay mặt phẳng có nhiều ứng dụng trong thực tế. Ví dụ như thiết kế mạng lưới giao thông, quy hoạch đô thị hay bố trí nhà máy.

Một nghiên cứu của Viện Quy hoạch Đô thị năm 2022 đã ứng dụng phương pháp tối ưu khoảng cách để thiết kế mạng lưới xe buýt tại Hà Nội, giúp giảm thời gian di chuyển và tăng hiệu quả vận chuyển hành khách.

Ngoài ra, trong logistics, việc tối ưu hóa khoảng cách vận chuyển giúp tiết kiệm chi phí nhiên liệu và thời gian giao hàng đáng kể.

Mối liên hệ giữa giá trị cực đại và giá trị tuyệt đối

Giá trị cực đại và giá trị tuyệt đối có mối liên hệ chặt chẽ trong toán học. giá trị tuyệt đối là gì đóng vai trò quan trọng khi xác định giá trị cực đại là y hay x trong nhiều bài toán phức tạp.

Khi phân tích một hàm số, việc xác định giá trị là x hay y phụ thuộc vào cách biểu diễn hàm số đó. Giá trị tuyệt đối có thể tác động đến vị trí cực đại, làm thay đổi dấu của biểu thức và ảnh hưởng đến kết quả cuối cùng.

So sánh giá trị cực đại và giá trị tuyệt đối

Giá trị cực đại thường được xác định thông qua việc tìm điểm có đạo hàm bằng 0 và kiểm tra sự thay đổi dấu của đạo hàm. Trong khi đó, giá trị tuyệt đối luôn không âm và có thể làm thay đổi tính chất của hàm số.

Một điểm khác biệt quan trọng là giá trị cực đại có thể âm hoặc dương, còn giá trị tuyệt đối luôn dương hoặc bằng 0. Điều này tạo ra sự khác biệt trong cách tiếp cận khi giải quyết các bài toán tối ưu.

Khi kết hợp cả hai khái niệm, việc tìm cực đại trở nên phức tạp hơn do cần xét các trường hợp khác nhau của dấu trong biểu thức chứa giá trị tuyệt đối.

Tìm cực trị của hàm có chứa giá trị tuyệt đối

Để tìm cực trị của hàm có chứa giá trị tuyệt đối, cần chia quá trình thành các bước cụ thể. Trước tiên, xác định các khoảng xét dấu của biểu thức bên trong dấu giá trị tuyệt đối.

Tiếp theo, viết lại biểu thức của hàm số theo từng khoảng đã xác định. Mỗi khoảng sẽ có một biểu thức tương ứng không chứa dấu giá trị tuyệt đối.

Sau khi có các biểu thức tương đương, áp dụng phương pháp tìm cực trị thông thường cho từng khoảng. Cuối cùng, so sánh các giá trị tìm được để xác định cực trị toàn cục của hàm số ban đầu.

Các dạng bài tập thường gặp về giá trị cực đại

Việc nắm vững các dạng bài tập về giá trị cực đại giúp học sinh phát triển tư duy toán học và kỹ năng giải quyết vấn đề. Mỗi dạng bài tập đều có những đặc điểm và phương pháp giải riêng, đòi hỏi sự linh hoạt trong cách tiếp cận.

Để giải quyết hiệu quả các bài toán về giá trị cực đại, học sinh cần nắm chắc kiến thức nền tảng về hàm số và đạo hàm. Việc tìm giá trị cực tiểu của hàm số thường đi kèm với việc tìm giá trị cực đại, tạo nên bức tranh toàn diện về tính chất của hàm số.

Tìm giá trị cực đại qua đạo hàm

Phương pháp sử dụng đạo hàm là cách phổ biến và hiệu quả nhất để tìm giá trị cực đại. Khi giá trị cực tiểu của hàm số đã cho bằng một giá trị cụ thể, ta có thể áp dụng các tính chất của đạo hàm để xác định điểm cực trị.

Việc xét dấu đạo hàm trước và sau điểm nghiệm giúp xác định chính xác loại cực trị. Nếu đạo hàm đổi dấu từ dương sang âm qua điểm nghiệm, điểm đó là cực đại của hàm số.

Khi áp dụng phương pháp này, cần chú ý đến miền xác định của hàm số và các điểm đặc biệt như điểm không khả vi hoặc điểm gián đoạn.

Suy luận giá trị cực đại từ đồ thị

Phương pháp suy luận giá trị cực đại từ đồ thị đòi hỏi khả năng quan sát và phân tích hình học tốt. Việc nhận diện các điểm uốn, điểm đặc biệt trên đồ thị giúp xác định nhanh vị trí có thể xuất hiện giá trị cực đại.

Khi phân tích đồ thị, cần chú ý đến tính đối xứng, tính tuần hoàn và các đặc điểm hình học khác. Những tính chất này thường cung cấp manh mối quan trọng về vị trí và giá trị của cực đại.

Việc kết hợp kiến thức về tính chất hàm số với quan sát đồ thị giúp kiểm chứng kết quả và tránh sai sót trong quá trình giải.

Bài tập về cực đại trong tam giác và tứ giác

Các bài toán về giá trị cực đại của hàm số trong hình học thường liên quan đến diện tích, chu vi hoặc các yếu tố đặc trưng khác của tam giác và tứ giác. Việc áp dụng các công thức hình học kết hợp với phương pháp tìm cực trị tạo nên những bài toán thú vị và thách thức.

Trong tam giác, các bài toán thường xoay quanh mối quan hệ giữa các cạnh, góc và diện tích. Việc thiết lập biểu thức hàm số phù hợp là bước quan trọng đầu tiên để tìm giá trị cực đại.

Đối với tứ giác, bài toán có thể phức tạp hơn do có nhiều yếu tố cần xét. Tuy nhiên, việc vận dụng các tính chất đặc biệt của tứ giác nội tiếp, ngoại tiếp hoặc tứ giác đều giúp đơn giản hóa quá trình giải

Như đã trình bày, giá trị cực đại là y hay x phụ thuộc vào việc phân tích và hiểu rõ hàm số. Việc áp dụng các phương pháp tìm cực trị, như xét dấu đạo hàm và kiểm tra điểm tới hạn, sẽ giúp bạn xác định được giá trị này một cách chính xác. Sự nắm vững kiến thức về cực đại không chỉ hỗ trợ trong việc giải các bài tập toán mà còn ứng dụng nhiều trong thực tiễn.