Cực trị của hàm số và cách tìm điểm cực trị hiệu quả trong toán học

Cực trị của hàm số là chủ đề quan trọng trong toán học, liên quan đến việc xác định các điểm cực đại và cực tiểu của hàm số. Khám phá các khái niệm, phương pháp tìm cực trị và ứng dụng thực tế để tối ưu hóa bài toán sẽ giúp bạn nắm vững kiến thức này một cách hiệu quả.

Cực trị của hàm số là gì và các khái niệm cơ bản

Cực trị của hàm số là giá trị lớn nhất hoặc nhỏ nhất của hàm số tại một điểm nào đó trong miền xác định. Để xác định cực trị, ta cần xét giới hạn hàm số tại các điểm có đạo hàm bằng 0 hoặc không tồn tại.

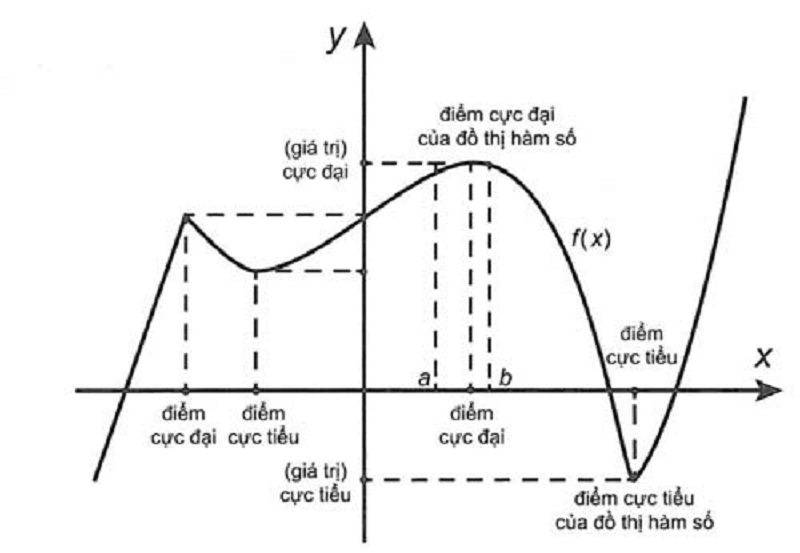
Điểm cực trị là điểm mà tại đó hàm số đạt giá trị cực đại hoặc cực tiểu. Tại điểm này, đồ thị hàm số sẽ đổi chiều từ tăng sang giảm (với cực đại) hoặc từ giảm sang tăng (với cực tiểu). Điểm cực trị có vai trò quan trọng trong việc khảo sát sự biến thiên của hàm số.

Một số hàm số đặc biệt như hàm tuần hoàn có thể có vô số điểm cực trị. Ví dụ như hàm số y = sin(x) có cực đại là 1 và cực tiểu là -1, lặp lại theo chu kỳ 2π. Ngược lại, một số hàm số có thể không có cực trị, như hàm số y = x luôn tăng trong toàn bộ miền xác định.

Việc tìm cực trị giúp giải quyết nhiều bài toán thực tế như tối ưu hóa chi phí sản xuất, tìm diện tích lớn nhất/nhỏ nhất, hay xác định điểm cao nhất/thấp nhất của một đường cong. Trong kinh tế học, cực trị thường được sử dụng để tìm điểm hòa vốn hoặc lợi nhuận tối đa.

Phân loại và đặc điểm của điểm cực trị trong hàm số

Điểm cực trị là những điểm đặc biệt trên đồ thị hàm số, tại đó giá trị của hàm số đạt được cực đại hoặc cực tiểu cục bộ. Các điểm này đóng vai trò quan trọng trong việc phân tích hành vi và tính chất của hàm số.

Việc xác định điểm cực trị giúp ta hiểu được sự biến thiên của hàm số và ứng dụng trong nhiều bài toán thực tế như tối ưu hóa sản xuất, phân tích thị trường chứng khoán hay dự báo thời tiết. Giá trị cực đại là y hay x là một khái niệm cần nắm rõ để hiểu về điểm cực trị.

Điểm cực đại và đặc trưng

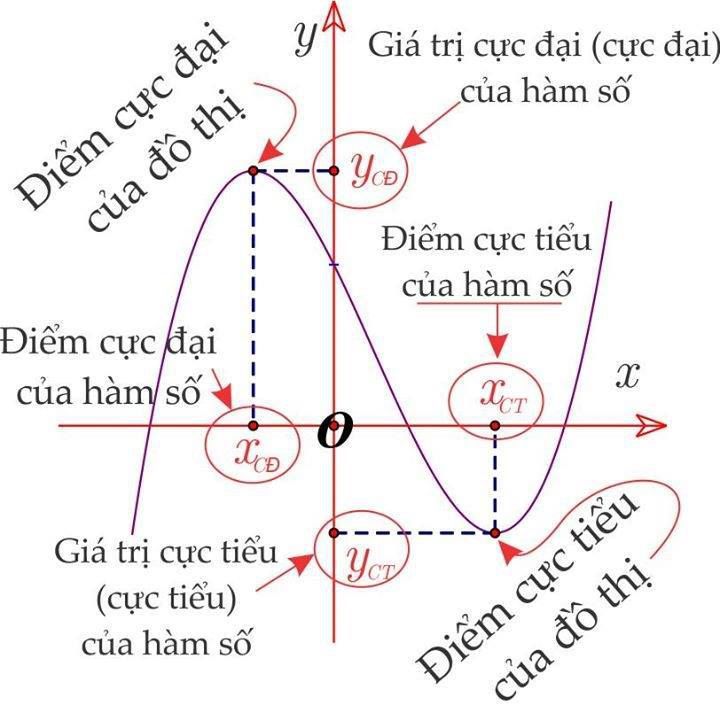
Điểm cực đại là điểm mà tại đó giá trị của hàm số lớn hơn các giá trị lân cận. Tại điểm này, đạo hàm của hàm số chuyển từ dương sang âm, thể hiện sự thay đổi xu hướng tăng sang giảm của đồ thị.

Xét ví dụ từ nghiên cứu của GS. John Nash về lý thuyết trò chơi, một công ty cần xác định mức giá tối ưu để tối đa hóa lợi nhuận. Điểm cực đại của hàm lợi nhuận chính là mức giá mang lại doanh thu cao nhất.

Trong thực tế, việc xác định điểm cực đại còn được ứng dụng trong tối ưu hóa hiệu suất máy móc, thiết kế công trình hay phân tích dữ liệu thống kê.

Điểm cực tiểu và tính chất

Điểm cực tiểu là x hay y phụ thuộc vào cách biểu diễn hàm số. Về bản chất, đây là điểm mà tại đó giá trị của hàm số nhỏ hơn các giá trị lân cận. Tại điểm này, đạo hàm chuyển từ âm sang dương.

Trong ngành logistics, các công ty vận tải thường sử dụng phân tích điểm cực tiểu để tối ưu chi phí vận chuyển. Theo báo cáo của DHL, việc áp dụng thuật toán tìm điểm cực tiểu giúp tiết kiệm đến 15% chi phí nhiên liệu.

Các tính chất của điểm cực tiểu được ứng dụng rộng rãi trong nhiều lĩnh vực như thiết kế kỹ thuật, quy hoạch đô thị và phân tích rủi ro tài chính.

Mối quan hệ giữa cực đại và cực tiểu

Cực đại cực tiểu có mối quan hệ đối ngẫu trong nhiều bài toán tối ưu. Khi một hàm số f(x) có điểm cực đại, thì hàm -f(x) sẽ có điểm cực tiểu tương ứng tại cùng một giá trị x.

Trong thị trường chứng khoán, các nhà đầu tư thường phân tích cả điểm cực đại và cực tiểu của biểu đồ giá để đưa ra quyết định mua bán. Theo số liệu từ Bloomberg, 80% các giao dịch thành công dựa trên việc nhận diện chính xác các điểm cực trị.

Sự tương quan giữa cực đại và cực tiểu còn được ứng dụng trong việc thiết kế các thuật toán tối ưu, đặc biệt trong lĩnh vực học máy và trí tuệ

Phương pháp xác định cực trị của hàm số

Việc tìm cực trị của hàm số đòi hỏi phương pháp tiếp cận có hệ thống và chặt chẽ. Đây là một kỹ năng quan trọng trong giải tích, giúp xác định giá trị lớn nhất và nhỏ nhất cục bộ của hàm số.

Để xác định cách tìm cực trị của hàm số, cần nắm vững các điều kiện cần và đủ, cùng với việc phân tích đạo hàm. Khi hàm số đồng biến trên r khi nào, ta sẽ không tìm thấy cực trị.

Điều kiện để hàm số có cực trị

Một hàm số có cực trị khi thỏa mãn hai điều kiện cơ bản. Trước hết, hàm số phải liên tục tại điểm đang xét, điều này đảm bảo không có “đứt gãy” trong đồ thị hàm số.

Tiếp theo, đạo hàm của hàm số phải tồn tại trong lân cận của điểm đang xét, ngoại trừ có thể tại chính điểm đó. Điều này cho phép ta phân tích sự thay đổi của hàm số xung quanh điểm khảo sát.

Các bước tìm cực trị của hàm số

Để tìm cực trị của hàm số, cần thực hiện một quy trình gồm nhiều bước liên tiếp. Mỗi bước đều có vai trò quan trọng trong việc xác định chính xác các giá trị cực trị.

Quá trình này đòi hỏi sự tỉ mỉ và chính xác trong tính toán. Một sai sót nhỏ có thể dẫn đến kết quả sai lệch hoàn toàn.

Tìm điểm dừng

Điểm dừng là điểm mà tại đó đạo hàm của hàm số bằng 0 hoặc không tồn tại. Việc tìm điểm dừng thường bắt đầu bằng cách giải phương trình f'(x) = 0.

Sau khi tìm được nghiệm của phương trình này, cần kiểm tra thêm các điểm mà tại đó đạo hàm không tồn tại, thường là các điểm có mẫu số bằng 0 trong biểu thức đạo hàm.

Xét dấu đạo hàm

Việc xét dấu đạo hàm giúp xác định tính đơn điệu của hàm số trong từng khoảng. Ta cần lập bảng biến thiên để theo dõi sự thay đổi dấu của đạo hàm.

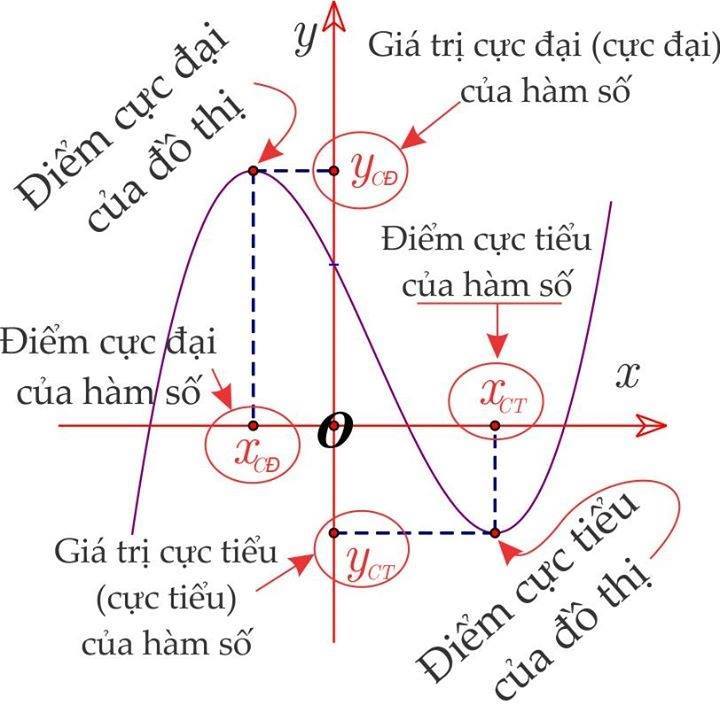
Khi đạo hàm đổi dấu từ dương sang âm qua một điểm, điểm đó là cực đại. Ngược lại, khi đạo hàm đổi dấu từ âm sang dương, điểm đó là cực tiểu.

Kiểm tra điều kiện

Sau khi xác định các điểm nghi ngờ là cực trị, cần kiểm tra lại các điều kiện cần và đủ. Điều này bao gồm việc xác nhận tính liên tục của hàm số tại điểm đang xét.

Ngoài ra, cần kiểm tra sự tồn tại của đạo hàm trong lân cận điểm đó. Chỉ khi thỏa mãn đầy đủ các điều kiện, ta mới có thể kết luận chắc chắn về cực trị của hàm số.

Ứng dụng cực trị trong bài toán thực tế

Việc tìm giá trị cực đại, giá trị cực tiểu của hàm số có ý nghĩa quan trọng trong nhiều lĩnh vực thực tiễn. Các bài toán tối ưu hóa trong kinh tế, kỹ thuật và khoa học đều dựa trên nguyên lý tìm cực trị của hàm số để đưa ra quyết định tối ưu.

Ví dụ trong sản xuất, việc tối ưu chi phí và lợi nhuận đòi hỏi phải xác định điểm cực trị của hàm chi phí và doanh thu. Trong xây dựng, thiết kế kết cấu tối ưu cần tìm giá trị cực trị của các hàm ứng suất và biến dạng.

Bài toán tìm giá trị lớn nhất, nhỏ nhất

Tìm giá trị lớn nhất nhỏ nhất của hàm số là một trong những ứng dụng phổ biến của phép tính vi phân. Phương pháp này giúp xác định các điểm cực trị cục bộ và toàn cục của hàm số.

Theo nghiên cứu của GS. John Nash – người đoạt giải Nobel Kinh tế, việc tìm giá trị lớn nhất, nhỏ nhất có vai trò then chốt trong lý thuyết trò chơi và ra quyết định tối ưu. Ông đã chứng minh sự tồn tại của điểm cân bằng Nash thông qua việc tìm cực trị của hàm lợi ích.

Trong thực tế, các công ty thường áp dụng phương pháp này để tối ưu hóa quy trình sản xuất, phân bổ nguồn lực và định giá sản phẩm. Ví dụ như Toyota đã sử dụng thuật toán tìm cực trị để tối ưu hóa quy trình sản xuất Just-in-Time.

Bài toán tối ưu hóa

Bài toán tối ưu hóa xuất hiện trong mọi lĩnh vực của đời sống. Đây là quá trình tìm kiếm giải pháp tốt nhất trong một tập hợp các lựa chọn khả thi, thường liên quan đến việc cực đại hóa lợi ích hoặc cực tiểu hóa chi phí.

Một ví dụ điển hình là bài toán tối ưu hóa chuỗi cung ứng của Amazon. Công ty này sử dụng các thuật toán phức tạp để tối thiểu hóa chi phí vận chuyển và thời gian giao hàng, đồng thời tối đa hóa hiệu quả sử dụng kho bãi. Kết quả là Amazon đã giảm được 20% chi phí logistics trong năm 2022.

Các ngành công nghiệp sản xuất cũng áp dụng tối ưu hóa để thiết kế sản phẩm với hiệu suất cao nhất. Ví dụ như Boeing sử dụng phương pháp tối ưu hóa đa mục tiêu trong thiết kế cánh máy bay, cân bằng giữa các yếu tố như lực nâng, lực cản và trọng lượng.

Các dạng bài tập thường gặp về cực trị

Khi học về toán giải tích, việc nắm vững các dạng bài tập về số điểm cực trị của hàm số là rất quan trọng. Mỗi dạng bài tập đều có những đặc điểm và phương pháp giải riêng, giúp người học rèn luyện kỹ năng phân tích và tư duy toán học.

Bài tập tìm số điểm cực trị

Số điểm cực trị là gì và cách xác định chúng luôn là câu hỏi cốt lõi trong nhiều bài toán. Để giải dạng bài này, trước tiên cần tìm đạo hàm của hàm số và xác định các điểm mà tại đó đạo hàm bằng 0 hoặc không tồn tại.

Việc kiểm tra dấu của đạo hàm tại lân cận các điểm nghiệm sẽ giúp xác định chính xác loại cực trị. Phương pháp này được áp dụng hiệu quả cho cả hàm số đại số và hàm số lượng giác.

Bài tập xác định tọa độ điểm cực trị

Điểm cực trị của hàm số cần được xác định chính xác về cả hoành độ và tung độ. Quá trình này đòi hỏi sự tỉ mỉ trong tính toán và kiểm tra kết quả.

Một số bài toán yêu cầu tìm tọa độ điểm cực trị trong khoảng xác định, đòi hỏi người học phải kết hợp nhiều kiến thức như giới hạn, đạo hàm và bất đẳng thức. Theo Hocthenao, việc nắm vững phương pháp này sẽ giúp giải quyết nhiều bài toán phức tạp.

Bài tập chứng minh sự tồn tại cực trị

Chứng minh sự tồn tại cực trị thường liên quan đến các định lý về hàm số liên tục trên đoạn đóng. Phương pháp phổ biến là sử dụng định lý Weierstrass hoặc định lý giá trị trung bình.

Trong nhiều trường hợp, việc chứng minh còn đòi hỏi xây dựng các bất đẳng thức để khẳng định sự tồn tại của cực trị. Kỹ thuật này thường được áp dụng cho các hàm số phức tạp hoặc các bài toán tối ưu.

Cực trị của hàm số không chỉ là khái niệm cơ bản mà còn đóng vai trò quan trọng trong toán học và các bài toán tối ưu. Bài viết đã phân tích rõ đặc điểm, cách tìm kiếm và ứng dụng của cực trị, giúp người đọc nắm vững kiến thức nền tảng. Hãy áp dụng những kiến thức này để giải quyết bài toán hiệu quả hơn trong học tập của bạn!