Tìm hiểu hai tam giác đồng dạng và tính chất ứng dụng trong hình học

Hai tam giác đồng dạng là khái niệm quan trọng trong hình học phẳng. Bài viết này sẽ giúp bạn khám phá các tính chất và dấu hiệu nhận biết của hai tam giác đồng dạng. Đồng thời, bạn cũng sẽ tìm hiểu phương pháp giải bài tập và ứng dụng thực tế của trong toán học. Hãy cùng tìm hiểu ngay!

Hai tam giác đồng dạng là hai tam giác có các góc tương ứng bằng nhau và tỷ lệ các cạnh tương ứng bằng nhau

Hai tam giác đồng dạng là hai tam giác có các góc tương ứng bằng nhau và các cạnh tương ứng tỷ lệ với nhau theo một tỷ số không đổi. Đây là một khái niệm quan trọng trong lý thuyết hình học phẳng giúp giải quyết nhiều bài toán phức tạp.

Khi xét về mặt hình học, tam giác đồng dạng là gì có thể hiểu như việc phóng to hoặc thu nhỏ một tam giác theo một tỷ lệ nhất định. Trong quá trình này, các góc của tam giác được giữ nguyên không thay đổi, trong khi các cạnh tương ứng sẽ thay đổi theo cùng một tỷ lệ.

Tính chất đồng dạng của hai tam giác được ứng dụng rộng rãi trong thực tế, từ việc vẽ bản đồ địa lý đến thiết kế kiến trúc. Ví dụ, khi kiến trúc sư thiết kế mô hình thu nhỏ của một công trình, họ sử dụng nguyên lý tam giác đồng dạng để đảm bảo tỷ lệ chính xác giữa mô hình và công trình thực tế.

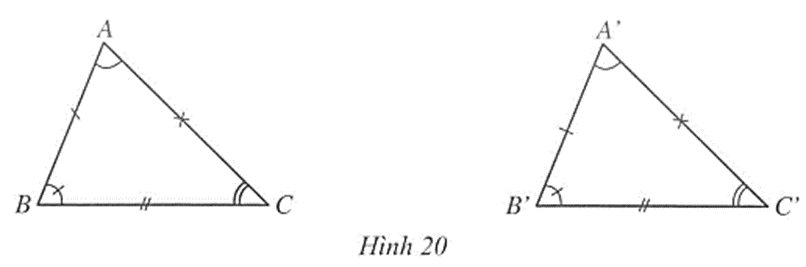
Việc xác định hai tam giác đồng dạng có thể dựa vào các tiêu chí như góc-góc (hai góc bằng nhau), cạnh-cạnh-cạnh (ba cặp cạnh tương ứng tỷ lệ), hay góc-cạnh-góc (hai góc và cạnh giữa chúng tỷ lệ). Những tiêu chí này tạo nên cơ sở vững chắc cho việc chứng minh và giải quyết các bài toán liên quan đến tam giác đồng dạng.

Các tính chất cơ bản của hai tam giác đồng dạng trong hình học phẳng

Tính chất tam giác đồng dạng là những đặc điểm quan trọng giúp xác định mối quan hệ giữa hai tam giác có hình dạng giống nhau nhưng kích thước có thể khác nhau. Các tính chất này có vai trò then chốt trong việc giải các bài toán hình học và ứng dụng thực tiễn.

Tính chất hai tam giác đồng dạng thể hiện mối liên hệ chặt chẽ giữa các yếu tố tương ứng của hai tam giác, từ đó tạo nên sự tương đồng về hình dạng. Việc nắm vững các tính chất của tam giác đồng dạng giúp đơn giản hóa nhiều bài toán phức tạp trong hình học.

Tỷ lệ các cạnh tương ứng bằng nhau

Khi hai tam giác đồng dạng, tỷ số độ dài các cạnh tương ứng luôn bằng nhau và bằng tỷ số đồng dạng k. Điều này có nghĩa là nếu ABC và A’B’C’ là hai tam giác đồng dạng thì: AB/A’B’ = BC/B’C’ = AC/A’C’ = k.

Tỷ số đồng dạng k này là hằng số không đổi và có ý nghĩa quan trọng trong việc tính toán các yếu tố còn lại của tam giác khi biết một số cạnh. Ví dụ, nếu một tam giác có các cạnh lần lượt là 3, 4, 5 thì tam giác đồng dạng với nó sẽ có các cạnh là 6, 8, 10 với tỷ số đồng dạng k = 2.

Các góc tương ứng bằng nhau

Trong hai tam giác đồng dạng, các góc tương ứng luôn bằng nhau. Đây là tính chất bất biến, không phụ thuộc vào kích thước của tam giác. Khi A = A’, B = B’, C = C’, hai tam giác ABC và A’B’C’ chắc chắn đồng dạng.

Tính chất này đặc biệt hữu ích trong việc chứng minh hai tam giác đồng dạng, bởi chỉ cần chứng minh được ba góc tương ứng bằng nhau là đủ điều kiện để kết luận về sự đồng dạng. Trong thực tế, tính chất này thường được áp dụng trong các bài toán về đo đạc gián tiếp.

Tỷ lệ diện tích và chu vi của hai tam giác đồng dạng

Khi hai tam giác đồng dạng với tỷ số đồng dạng k, tỷ số diện tích của chúng bằng bình phương của tỷ số đồng dạng (k²). Điều này có nghĩa nếu S và S’ lần lượt là diện tích của hai tam giác thì S/S’ = k².

Về chu vi, tỷ số chu vi của hai tam giác đồng dạng bằng chính tỷ số đồng dạng k. Nếu P và P’ lần lượt là chu vi của hai tam giác thì P/P’ = k. Những tính chất này rất quan trọng trong các bài toán thực tế liên quan đến tỷ lệ xích và bản đồ địa hình.

Các dấu hiệu nhận biết và chứng minh hai tam giác đồng dạng

Để chứng minh hai tam giác đồng dạng, ta cần dựa vào các dấu hiệu tam giác đồng dạng cơ bản. Các dấu hiệu này giúp xác định mối quan hệ tỷ lệ giữa các cạnh tương ứng và sự bằng nhau của các góc tương ứng. Việc áp dụng đúng các dấu đồng dạng sẽ giúp giải quyết nhiều bài toán hình học phức tạp một cách hiệu quả.

Dấu hiệu góc – góc (g.g)

Dấu hiệu góc – góc là trường hợp đơn giản nhất để chứng minh hai tam giác đồng dạng. Khi hai tam giác có hai góc bằng nhau thì góc thứ ba cũng bằng nhau và hai tam giác đó đồng dạng. Điều này xuất phát từ tính chất tổng ba góc trong tam giác bằng 180°.

Ví dụ trong thực tế, các kiến trúc sư thường áp dụng dấu hiệu này khi thiết kế các công trình có tỷ lệ thu nhỏ. Họ chỉ cần đảm bảo các góc giữa mô hình và công trình thật bằng nhau, các kích thước sẽ tự động tỷ lệ với nhau.

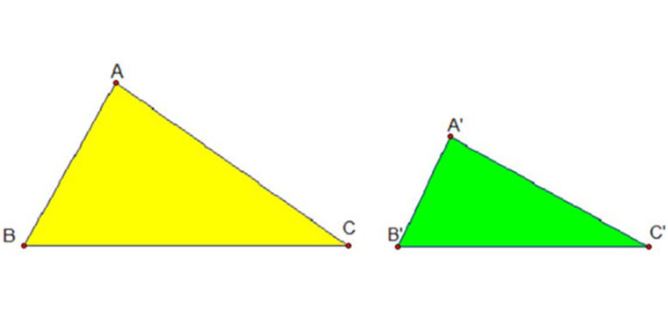
Dấu hiệu cạnh – cạnh – cạnh (c.c.c)

Khi tỷ số độ dài các cạnh tương ứng của hai tam giác bằng nhau, ta có thể kết luận hai tam giác đó đồng dạng. Đây là một trong những trường hợp đồng dạng của tam giác vuông phổ biến.

Trong công nghệ in 3D, nguyên lý này được ứng dụng để tạo ra các mô hình có kích thước khác nhau nhưng vẫn giữ nguyên hình dạng. Máy in sẽ điều chỉnh tỷ lệ các cạnh một cách đồng bộ để đảm bảo tính đồng dạng của sản phẩm.

Dấu hiệu góc – cạnh – góc (g.c.g)

Dấu hiệu góc – cạnh – góc xác định rằng hai tam giác đồng dạng khi chúng có hai góc và cạnh giữa hai góc đó tỷ lệ với nhau. Đây là dấu hiệu thường được sử dụng trong các bài toán phức tạp về đồng dạng.

Trong ngành đo đạc địa hình, các kỹ sư thường áp dụng dấu hiệu này khi sử dụng máy kinh vĩ để đo góc và khoảng cách. Bằng cách đo hai góc và một cạnh, họ có thể xác định được vị trí và khoảng cách của các điểm còn lại trên bản đồ dựa vào tính chất đồng dạng.

Phương pháp giải các bài toán về hai tam giác đồng dạng

Để giải các bài toán liên quan đến hai tam giác đồng dạng, cần nắm vững các phương pháp và công thức cơ bản. Việc áp dụng đúng phương pháp sẽ giúp giải quyết nhanh chóng và chính xác các dạng bài tập.

Khi xử lý các bài toán này, trước tiên cần xác định rõ các yếu tố đã biết và cần tìm. Sau đó, áp dụng các định lý và tính chất phù hợp để chứng minh hoặc tính toán. Dưới đây là các phương pháp chính để giải quyết các bài tập tam giác đồng dạng.

Các công thức tính toán cơ bản

Khi hai tam giác đồng dạng, tỷ số các cạnh tương ứng bằng nhau và được gọi là tỷ số đồng dạng k. Các góc tương ứng của hai tam giác bằng nhau.

Diện tích hai tam giác đồng dạng có tỷ số bằng bình phương của tỷ số đồng dạng: S1/S2 = k². Điều này giúp giải quyết nhiều bài toán về diện tích.

Chu vi hai tam giác đồng dạng có tỷ số bằng tỷ số đồng dạng: P1/P2 = k. Các 2 góc phụ nhau là gì cũng là một kiến thức quan trọng khi giải các bài toán về góc.

Phương pháp chứng minh đồng dạng

Để chứng minh hai tam giác đồng dạng, có thể sử dụng các tiêu chuẩn đồng dạng: góc-góc (g.g), cạnh-góc-cạnh (c.g.c), cạnh-cạnh-cạnh (c.c.c).

Trong nhiều trường hợp, cần vẽ thêm các đường phụ để tạo ra các tam giác đồng dạng. Việc này giúp phát hiện các yếu tố chưa biết một cách gián tiếp.

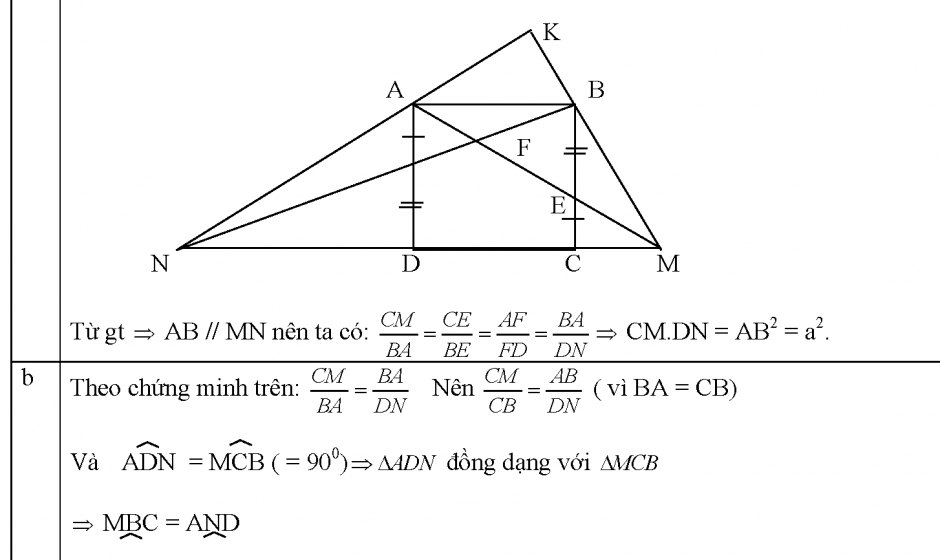
Khi áp dụng các tiêu chuẩn, cần chỉ ra đầy đủ các yếu tố tương ứng và lập luận chặt chẽ để chứng minh tính đồng dạng của công thức tam giác đồng dạng.

Cách tìm các yếu tố chưa biết

Sau khi chứng minh được hai tam giác đồng dạng, việc tìm các yếu tố chưa biết trở nên dễ dàng hơn. Có thể sử dụng tỷ số đồng dạng để thiết lập các phương trình.

Trong một số bài toán phức tạp, cần kết hợp nhiều phương pháp như: sử dụng định lý Pythagoras, định lý sin, định lý cosin để tìm các yếu tố trung gian.

Việc vẽ hình chính xác và ghi chú đầy đủ các yếu tố đã biết sẽ giúp quá trình tìm kiếm các yếu tố chưa biết được thuận lợi và tránh sai sót.

Ứng dụng của hai tam giác đồng dạng trong thực tế và các bài toán hình học

Hai tam giác đồng dạng có nhiều ứng dụng quan trọng trong thực tế và toán học. Chúng giúp giải quyết các bài toán về đo đạc, xây dựng và thiết kế một cách hiệu quả. Việc áp dụng tính chất của các tam giác tương tự còn liên quan mật thiết đến các hình đa diện trong không gian ba chiều.

Các ứng dụng của so sánh tam giác đồng dạng được thể hiện rõ nét trong ba lĩnh vực chính: tính toán khoảng cách và chiều cao, giải quyết các bài toán về tỷ lệ, cũng như ứng dụng trong xây dựng và kiến trúc. Mỗi lĩnh vực đều có những đặc thù riêng và cách tiếp cận phù hợp.

Tính khoảng cách và chiều cao

Phương pháp sử dụng tam giác đồng dạng để đo khoảng cách và chiều cao đã được áp dụng từ thời cổ đại. Kỹ thuật này đặc biệt hữu ích khi cần đo các khoảng cách lớn hoặc độ cao của các công trình mà không thể tiếp cận trực tiếp.

Một ví dụ điển hình là phương pháp đo chiều cao tháp của Thales. Ông đã sử dụng bóng của cây gậy và bóng của tháp để tạo nên hai tam giác đồng dạng, từ đó tính được chiều cao tháp một cách chính xác. Phương pháp này vẫn được áp dụng trong các công trình hiện đại.

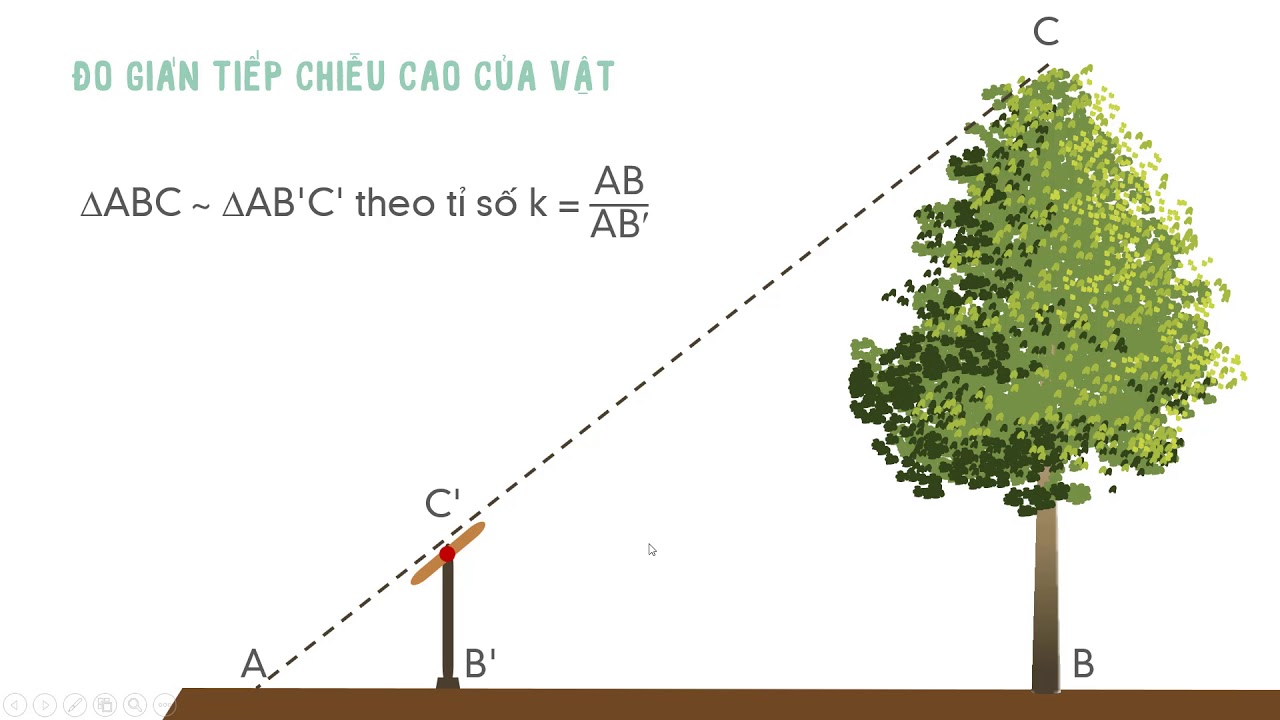
Trong trắc địa, các kỹ sư thường sử dụng nguyên lý này kết hợp với điều kiện để 3 vecto đồng phẳng để đo đạc địa hình phức tạp một cách hiệu quả.

Giải các bài toán về tỷ lệ

Trong thiết kế và chế tạo, ứng dụng tam giác đồng dạng giúp tạo ra các mô hình thu nhỏ hoặc phóng to chính xác. Các nhà thiết kế sử dụng tính chất bảo toàn tỷ lệ của tam giác đồng dạng để đảm bảo tính thẩm mỹ và cân đối của sản phẩm.

Công nghiệp điện tử sử dụng nguyên lý này trong việc thiết kế mạch in và bo mạch. Các kỹ sư có thể tạo ra những bản thiết kế chi tiết ở tỷ lệ lớn hơn, sau đó thu nhỏ xuống kích thước thực tế mà vẫn giữ nguyên các tỷ lệ quan trọng.

Ứng dụng trong xây dựng và kiến trúc

Kiến trúc sư Frank Gehry đã áp dụng nguyên lý tam giác đồng dạng trong thiết kế Bảo tàng Guggenheim Bilbao. Các mặt của công trình được tạo thành từ nhiều tam giác đồng dạng, tạo nên một tổng thể hài hòa và độc đáo.

Trong xây dựng cầu treo, kỹ sư sử dụng tam giác đồng dạng để thiết kế hệ thống dây văng. Việc bố trí các dây theo nguyên lý này giúp phân phối lực đều và tăng độ ổn định cho công trình. Ví dụ như cầu Cần Thơ, các dây văng được bố trí tạo

Khi nói đến hai tam giác đồng dạng, chúng ta đang đề cập đến một khái niệm cực kỳ quan trọng trong hình học. Những tính chất này không chỉ giúp xác định mối quan hệ giữa các tam giác mà còn được ứng dụng rộng rãi trong thực tiễn. Việc nắm vững các dấu hiệu và tính chất của tam giác đồng dạng sẽ hỗ trợ bạn trong việc giải quyết nhiều bài toán hình học phức tạp và hiểu sâu hơn về cấu trúc không gian.