Hệ thức truy hồi trong toán rời rạc: Lý thuyết và bài tập

Hệ thức truy hồi là một công cụ toán học phổ biến thường được dùng để mô tả các dãy số, cấu trúc dữ liệu và các quy trình lặp đi lặp lại. Nó được ứng dụng trong nhiều lĩnh vực, từ khoa học máy tính đến toán học, kinh tế và sinh học. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về hệ thức này, bao gồm định nghĩa, ứng dụng và ví dụ minh họa.

Hệ thức truy hồi là gì?

Hệ thức truy hồi là một tập hợp các phương trình mô tả mối quan hệ giữa các số hạng trong một dãy số. Nó bao gồm hai phần chính:

• Số hạng đầu: Là giá trị khởi tạo cho dãy số.
• Công thức truy hồi: Là quy tắc để tính toán các số hạng tiếp theo dựa trên các số hạng trước đó.

Dạng của hệ thức thuần nhất tuyến tính bậc k với hệ số hằng có dạng:

$$a_n\;=\;c_1a_{n-1}\;+\;c_2a_{n-2}\;+…+\;c_ka_{n-k}$$

Trong đó, c1, c2, c3,… ck là hằng số thực khác 0.

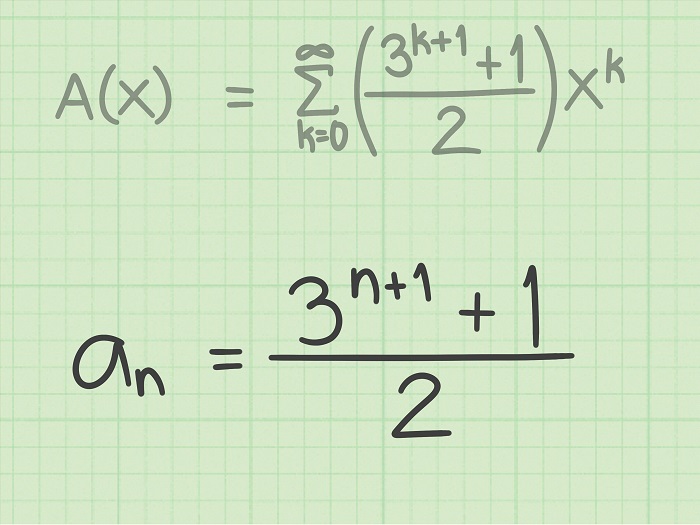
Cách thức hoạt động

Để sử dụng hệ thức truy hồi, ta cần thực hiện các bước sau:

• Bước 1. Xác định số hạng đầu: Giá trị này được cung cấp sẵn hoặc tính toán dựa trên một quy tắc cụ thể.
• Bước 2. Áp dụng công thức truy hồi: Sử dụng công thức để tính toán các số hạng tiếp theo của dãy số. Lặp lại bước này cho đến khi đạt được số hạng mong muốn hoặc đáp ứng điều kiện kết thúc.

Công thức truy hồi là gì?

Công thức truy hồi được sử dụng để mô tả mối quan hệ giữa các số hạng trong một dãy số. Nó là một quy tắc toán học giúp tính toán các số hạng tiếp theo của dãy số dựa trên các số hạng trước đó.

Ví dụ:

Dãy Fibonacci: Dãy Fibonacci được mô tả bởi công thức truy hồi sau:

• F(0) = 0
• F(1) = 1
• F(n) = F(n-1) + F(n-2), n > 1

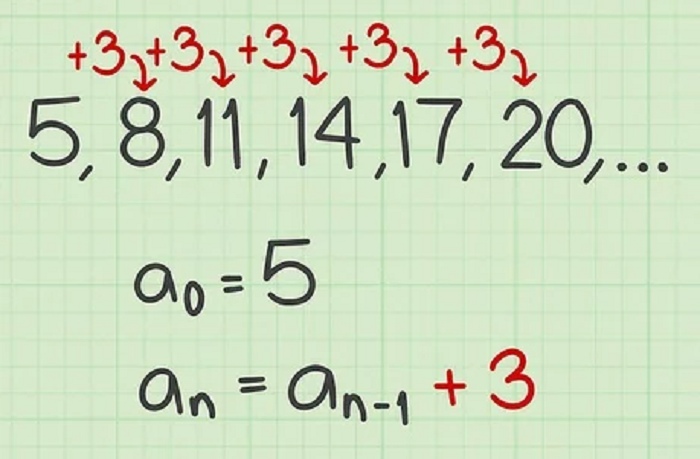
Cách giải hệ thức truy hồi

Trong hệ thức truy hồi, mỗi số hạng trong dãy số được biểu thị bằng tích của một hằng số a và lũy thừa của số hạng trước đó. Dạng hệ thức truy hồi này thường được sử dụng để mô tả các dãy số có tỷ lệ tăng trưởng hoặc giảm đều đặn.

Cách giải:

Để giải hệ thức truy hồi dạng an, ta có thể sử dụng các phương pháp sau:

• Phương pháp quy nạp: Phương pháp này dựa trên nguyên tắc chứng minh rằng công thức truy hồi đúng cho một số giá trị ban đầu (thường là n = 1) và sau đó chứng minh rằng nếu công thức đúng cho n = k thì nó cũng đúng cho n = k + 1.
• Phương pháp biến đổi: Phương pháp này sử dụng các phép biến đổi toán học để đưa hệ thức truy hồi về dạng đơn giản hơn, từ đó có thể tìm ra công thức tổng quát cho dãy số.

Ưu điểm và nhược điểm của hệ thức truy hồi

Việc áp dụng hệ thức truy hồi toán rời rạc có những ưu và nhược điểm như sau:

Ưu điểm:

• Hệ thức này cung cấp cách tiếp cận trực quan và dễ hiểu để mô tả các dãy số, đặc biệt là những dãy số có cấu trúc phức tạp.
• Nó có tính linh hoạt cao, cho phép mô tả nhiều loại dãy số khác nhau.
• Hệ thức có thể được sử dụng để giải quyết các bài toán đệ quy một cách hiệu quả.

Nhược điểm:

• Việc xác định số hạng đầu và công thức truy hồi phù hợp cho một dãy số cụ thể có thể gặp khó khăn.
• Hệ thức sẽ dẫn đến các vấn đề hiệu suất nếu không được triển khai một cách cẩn thận.

Ứng dụng của hệ thức truy hồi

Hệ thức truy hồi được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:

• Khoa học máy tính: Lập trình đệ quy, giải thuật tìm kiếm, tối ưu hóa, xử lý ngôn ngữ tự nhiên,…
• Toán học: Dãy Fibonacci, số Catalan, fractals…
• Kinh tế: Mô hình hóa thị trường tài chính, dự báo nhu cầu,…
• Sinh học: Mô hình hóa sự phát triển của sinh vật, phân tích trình tự DNA,…

Một số bài tập về giải hệ thức truy hồi

Dưới đây là một số bài tập về giải hệ thức truy hồi mà chúng tôi đã tổng hợp được, giúp bạn hiểu rõ hơn về dạng bài tập này:

Bài tập 1:

Dãy số 1, 2, 4, 8, 16, … là một dãy số có tỷ lệ tăng trưởng gấp đôi sau mỗi số hạng. Dãy số này có thể được mô tả bởi hệ thức truy hồi dạng an sau:

• a1 = 1
• an = 2 x an-1

Giải hệ thức này bằng phương pháp quy nạp:

• Bước 1: Chứng minh công thức đúng cho n = 1.

Thay n = 1 vào hệ thức, ta được: a1 = 2 x a0

Vì a1 = 1 và a0 là số hạng trước a1, ta có thể giả sử a0 = 1/2.

Thay a0 = 1/2 vào phương trình trên, ta được: 1 = 2 x 1/2

=> Phương trình đúng.

• Bước 2: Giả sử công thức đúng cho n = k.
  • Thay n = k vào hệ thức, ta được: ak = 2 x ak-1
• Bước 3: Chứng minh công thức cũng đúng cho n = k + 1.
  • Thay n = k + 1 vào hệ thức, ta được: ak+1 = 2 x ak
  • Thay ak = 2 x ak-1 vào phương trình trên, ta được:
    • ak+1 = 2 x (2 x ak-1)
    • ak+1 = 4 x ak-1

Vì ak-1 là số hạng trước ak+1, ta có thể giả sử ak+1 = 4 x ak-1.

• • Thay ak+1 = 4 x ak-1 vào phương trình trên, ta được:
    • 4 x ak-1 = 4 x ak-1

=> Phương trình đúng.

Kết luận:

Qua hai bước trên, ta đã chứng minh được công thức: $$an=2^{(n-1)}$$ là công thức tổng quát cho dãy số 1, 2, 4, 8, 16, ….

Bài tập 2:

Dãy số 1/2, 1/4, 1/8, 1/16, 1/32, … là một dãy số có tỷ lệ giảm một nửa sau mỗi số hạng. Dãy số này có thể được mô tả bởi hệ thức truy hồi dạng an sau:

• a1 = 1/2
• an = 1/2 x an-1

Giải hệ thức bằng phương pháp biến đổi:

• Thay an = 1/2 x an-1 vào phương trình an = a1 x n^k, ta được:
  • 1/2 x an-1 = a1 x n^k
  • an-1 = 2 x a1 x n^k
• Thay an-1 = 2 x a1 x n^k vào phương trình an = 1/2 x an-1, ta được:
  • an = 1/2 x (2 x a1 x n^k)
  • an = a1 x n^k

Kết luận:

Qua phép biến đổi trên, ta đã tìm được công thức tổng quát cho dãy số 1/2, 1/4, 1/8, 1/16, 1/32, … là an = 1/2^n

Bài tập 3:

Dãy số Fibonacci, được mô tả bởi hệ thức truy hồi sau:

• a1 = 0
• a2 = 1
• an = an-1 + an-2, n > 2

Giải hệ thức bằng phương pháp quy nạp:

• Bước 1: Chứng minh công thức đúng cho n = 1 và n = 2.

Thay n = 1 vào hệ thức truy hồi, ta được: a1 = a0 + a0

Vì a1 = 0 và a0 là số hạng trước a1, ta có thể giả sử a0 = 0.

Thay a0 = 0 vào phương trình trên, ta được:

0 = 0 + 0

=> Phương trình đúng.

Thay n = 2 vào hệ thức truy hồi, ta được: a2 = a1 + a0

Vì a2 = 1 và a1 = 0 (đã chứng minh ở bước 1), ta có thể giả sử a0 = 1.

Thay a0 = 1 vào phương trình trên, ta được: 1 = 0 + 1

=> Phương trình đúng.

• Bước 2: Giả sử công thức đúng cho n = k.

Thay n = k vào hệ thức, ta được: ak = ak-1 + ak-2

• Bước 3: Chứng minh công thức cũng đúng cho n = k + 1.

Thay n = k + 1 vào hệ thức, ta được: ak+1 = ak + ak-1

Thay ak = ak-1 + ak-2 (đã chứng minh ở bước 2) vào phương trình trên, ta được:

• ak+1 = (ak-1 + ak-2) + ak-1
• ak+1 = 2 x ak-1 + ak-2

Vì ak-1 và ak-2 là hai số hạng trước ak+1, ta có thể giả sử ak+1 = 2 x ak-1 + ak-2.

Thay ak+1 = 2 x ak-1 + ak-2 vào phương trình trên, ta được:

2 x ak-1 + ak-2 = 2 x ak-1 + ak-2

=> Phương trình đúng.

Kết luận:

Qua hai bước trên, ta đã chứng minh được công thức an = Fn là công thức tổng quát cho dãy số Fibonacci, trong đó Fn là số Fibonacci thứ n.

Lời kết

Trên đây là toàn bộ những thông tin về khái niệm, cách giải hệ thức truy hồi trong toán rời rạc. Bên cạnh đó, chúng tôi cũng đã cung cấp cho bạn một số ví dụ minh hoạ về dạng bài tập này. Mong rằng qua bài viết này, bạn có thể nắm vững lý thuyết cũng như cách giải bài tập trong dạng toán này. Chúc các bạn học tốt!