Hình chóp cụt là gì? Định nghĩa, đặc điểm và ứng dụng trong toán học

Hình chóp cụt là gì? Đây là một trong những khái niệm quan trọng trong hình học không gian. Thông qua bài viết này, bạn sẽ khám phá các định nghĩa, đặc điểm và ứng dụng thực tiễn của hình chóp cụt. Ngoài ra, chúng tôi cũng cung cấp công thức tính toán cho thể tích và diện tích, giúp bạn giải quyết bài tập hiệu quả.

Hình chóp cụt là gì?

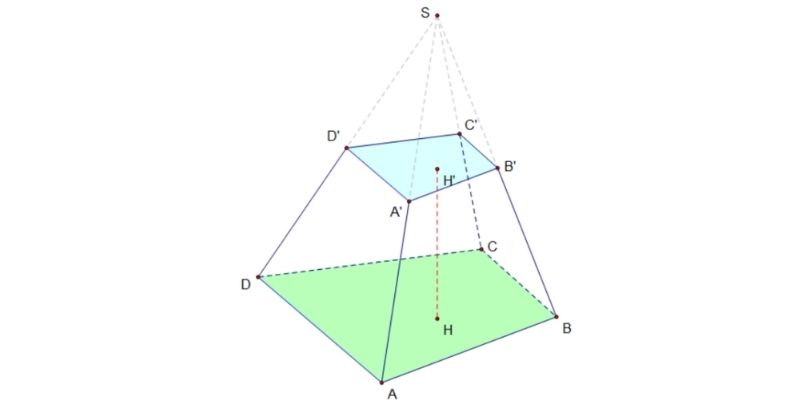
Hình chóp cụt là khối đa diện được tạo thành khi cắt một hình chóp bởi một mặt phẳng song song với đáy và nằm giữa đáy và đỉnh của hình chóp. Phần còn lại sau khi cắt sẽ tạo thành một hình chóp cụt với hai mặt đáy song song và không bằng nhau.

Về cấu tạo, một hình chóp cụt bao gồm hai mặt đáy song song là hai đa giác đồng dạng, các mặt bên là các hình thang và các cạnh bên không đồng quy tại một điểm như hình chóp thông thường. Các cạnh bên của hình chóp cụt song song với các cạnh bên tương ứng của hình chóp ban đầu.

Trong thực tế, hình chóp cụt xuất hiện phổ biến trong kiến trúc và xây dựng. Ví dụ như phần thân của tháp Eiffel ở Paris được thiết kế dựa trên nguyên lý hình chóp cụt, giúp công trình vừa có tính thẩm mỹ vừa đảm bảo độ vững chắc. Các công trình kim tự tháp ở Ai Cập khi bị mất phần đỉnh cũng tạo thành hình chóp cụt điển hình.

Đặc điểm và cấu tạo của hình chóp cụt trong không gian ba chiều

Đặc điểm của hình chóp cụt được xác định bởi một khối hình học đặc biệt, tạo thành khi cắt một hình chóp bởi mặt phẳng song song với đáy và không đi qua đỉnh. Cấu trúc này tạo nên một hình khối độc đáo trong hình chóp cụt trong hình học không gian, với hai mặt đáy song song và các mặt bên là hình thang.

Để hiểu rõ hơn về cấu tạo của hình chóp cụt, ta cần phân tích chi tiết các thành phần cơ bản và mối quan hệ giữa chúng. Tương tự như điểm uốn trong đồ thị hàm số, việc cắt hình chóp tạo ra một sự thay đổi đột ngột trong cấu trúc hình học ban đầu.

Các yếu tố cơ bản của hình chóp cụt

Hình chóp cụt bao gồm hai mặt đáy song song có hình dạng đồng dạng nhưng kích thước khác nhau. Đáy lớn thường được gọi là đáy chính, trong khi đáy nhỏ hơn được gọi là mặt cắt.

Chiều cao của hình chóp cụt được xác định bởi khoảng cách giữa hai mặt phẳng chứa hai đáy. Đây là yếu tố quan trọng ảnh hưởng trực tiếp đến thể tích và các tính chất hình học khác của hình chóp cụt.

Các cạnh bên của hình chóp cụt không còn gặp nhau tại một điểm như hình chóp thông thường, mà thay vào đó tạo thành các đoạn thẳng nối các đỉnh tương ứng của hai đáy.

Mối quan hệ giữa hai đáy song song

Hai đáy của hình chóp cụt luôn đồng dạng và song song với nhau. Tỷ số đồng dạng giữa hai đáy phụ thuộc vào vị trí mặt phẳng cắt so với đỉnh của hình chóp ban đầu.

Các cạnh và góc tương ứng trên hai đáy có tỷ lệ không đổi. Điều này tạo ra một quy luật quan trọng trong việc tính toán các yếu tố của hình chóp cụt.

Diện tích của hai đáy có mối quan hệ bình phương với tỷ số đồng dạng. Đây là một tính chất đặc biệt giúp đơn giản hóa nhiều bài toán liên quan đến hình chóp cụt.

Các cạnh bên và mặt bên của hình chóp cụt

Mỗi mặt bên của hình chóp cụt là một hình thang. Các cạnh song song của hình thang này chính là các cạnh tương ứng của hai đáy, trong khi hai cạnh không song song là các cạnh bên của hình chóp cụt.

Các cạnh bên của hình chóp cụt không song song với nhau như trong hình chóp thường. Chúng tạo với mặt phẳng đáy những góc khác nhau, phụ thuộc vào vị trí của chúng trong hình chóp ban đầu.

Tổng diện tích các mặt bên tạo thành diện tích xung quanh của hình chóp cụt. Việc tính toán diện tích này thường được thực hiện thông qua tổng diện tích các hình thang bên.

Phân loại và dạng đặc biệt của hình chóp cụt

Phân loại hình chóp cụt dựa trên hình dạng của đáy và mặt cắt song song với đáy. Khi hai mặt đáy song song có cùng dạng hình học nhưng kích thước khác nhau, ta có hình chóp cụt có đáy song song. Theo Học Thế Nào, việc phân loại này giúp việc tính toán diện tích và thể tích trở nên dễ dàng hơn.

Hình chóp cụt có đáy là hình vuông

Hình chóp cụt có đáy là hình vuông được tạo thành khi cắt một hình chóp có đáy là hình vuông bởi một mặt phẳng song song với đáy. Đặc điểm quan trọng là các cạnh bên không vuông góc với đáy, tạo thành các mặt bên là hình thang.

Trong thực tế, hình dạng này thường xuất hiện trong kiến trúc kim tự tháp cổ đại của người Ai Cập. Các khối đá được xếp chồng lên nhau, thu nhỏ dần về phía đỉnh tạo thành hình chóp cụt hoàn chỉnh.

Hình chóp cụt có đáy là hình tròn

Hình chóp cụt có đáy là hình tròn được tạo ra khi cắt một hình nón bởi một mặt phẳng song song với đáy. Đây là dạng hình học phổ biến trong công nghiệp, đặc biệt là thiết kế các ống khói, phễu, và bình chứa.

Ứng dụng thực tiễn của hình dạng này có thể thấy trong thiết kế của các ống khói nhà máy. Phần đáy rộng hơn giúp tăng độ ổn định, trong khi phần trên thu nhỏ lại giúp tăng tốc độ thoát khí.

Hình chóp cụt có đáy là đa giác đều

Hình chóp cụt có đáy là đa giác đều được tạo thành khi cắt một hình chóp có đáy là đa giác đều bởi một mặt phẳng song song với đáy. Các mặt bên của hình chóp cụt này là những hình thang cân đồng dạng.

Trong công nghiệp đóng gói, hình dạng này thường được sử dụng để thiết kế các hộp đựng sản phẩm có khả năng xếp chồng. Các cạnh nghiêng giúp sản phẩm dễ dàng tháo khỏi khuôn đúc và tăng độ bền của bao bì.

Việc hiểu rõ đặc điểm của từng loại hình chóp cụt giúp tối ưu hóa việc ứng dụng trong thực tế, từ thiết kế công trình đến sản xuất công nghiệp.

Công thức tính toán các yếu tố của hình chóp cụt

Để tính toán chính xác các yếu tố của hình chóp cụt, cần nắm vững các công thức tính diện tích hình chóp cụt và thể tích hình chóp cụt. Các công thức này giúp giải quyết nhiều bài toán thực tiễn trong kiến trúc, xây dựng và thiết kế.

Việc tính toán các yếu tố của hình chóp cụt đòi hỏi sự chính xác và áp dụng đúng công thức. Bạn có thể tham khảo thêm công thức diện tích hình chóp cụt để hiểu rõ hơn về cách áp dụng.

Công thức tính diện tích xung quanh

Diện tích xung quanh của hình chóp cụt được tính bằng tổng diện tích các mặt bên. Mỗi mặt bên là một hình thang với đáy lớn và đáy nhỏ tương ứng với các cạnh của đáy lớn và đáy nhỏ của hình chóp cụt.

Công thức tổng quát: Sxq = P.h/2, trong đó P là tổng các đường cao của các hình thang bên, h là chiều cao của hình thang bên. Đối với hình chóp cụt đều, công thức được viết gọn là: Sxq = (P1 + P2).l/2, với P1, P2 là chu vi đáy lớn và đáy nhỏ, l là độ dài đường sinh.

Công thức tính diện tích toàn phần

Diện tích toàn phần của hình chóp cụt bằng tổng diện tích xung quanh và diện tích hai đáy. Công thức này áp dụng cho mọi loại hình chóp cụt, không phân biệt đều hay không đều.

Với hình chóp cụt có đáy là đa giác đều n cạnh, diện tích toàn phần được tính theo công thức: St = Sxq + S1 + S2. Trong đó S1, S2 lần lượt là diện tích đáy lớn và đáy nhỏ của hình chóp cụt.

Công thức tính thể tích

Thể tích hình chóp cụt được tính theo công thức: V = (h/3)(S1 + S2 + √(S1.S2)). Trong đó h là chiều cao hình chóp cụt, S1 và S2 là diện tích đáy lớn và đáy nhỏ.

Công thức này có nguồn gốc từ phép tính tích phân và được ứng dụng rộng rãi trong thực tế. Ví dụ, khi tính thể tích của bể chứa nước hình chóp cụt tại nhà máy thủy điện Sơn La, kỹ sư đã áp dụng công thức này để tính toán chính xác lượng nước có thể chứa.

Ứng dụng thực tiễn của hình chóp cụt trong đời sống và kỹ thuật

Ứng dụng hình chóp cụt xuất hiện phổ biến trong nhiều lĩnh vực của cuộc sống, từ kiến trúc đến công nghiệp sản xuất. Hình dạng đặc trưng này mang lại tính thẩm mỹ và công năng vượt trội, đồng thời đảm bảo độ bền vững cho các công trình và sản phẩm. Để tính toán chính xác kích thước khi thiết kế, các kỹ sư thường sử dụng công thức chu vi hình chóp cụt làm cơ sở.

Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc, hình chóp cụt được ứng dụng rộng rãi để tạo nên những công trình độc đáo và ấn tượng. Các kim tự tháp cổ đại ở Ai Cập là minh chứng điển hình cho việc sử dụng hình chóp cụt trong xây dựng từ thời cổ đại. Cấu trúc này giúp phân bố trọng lượng đều và tăng độ ổn định cho công trình.

Ngày nay, nhiều tòa nhà hiện đại cũng áp dụng nguyên lý thiết kế này, như tháp Transamerica ở San Francisco với phần thân thu nhỏ dần về phía đỉnh. Kiểu thiết kế này không chỉ tạo điểm nhấn về mặt thẩm mỹ mà còn giúp giảm tác động của gió lên công trình cao tầng.

Ứng dụng trong công nghiệp và sản xuất

Trong ngành công nghiệp, ứng dụng của hình chóp cụt thể hiện rõ qua việc thiết kế các phễu chứa, bunker và thùng chứa vật liệu. Hình dạng này cho phép vật liệu di chuyển dễ dàng từ trên xuống dưới nhờ tác dụng của trọng lực, đồng thời tránh tình trạng tắc nghẽn.

Các nhà máy xi măng thường sử dụng silô hình chóp cụt để lưu trữ nguyên liệu. Theo số liệu từ Hiệp hội Xi măng Việt Nam, thiết kế này giúp tăng hiệu quả lưu trữ lên 30% và giảm chi phí vận hành khoảng 15% so với các dạng thùng chứa truyền thống.

Ứng dụng trong thiết kế và mỹ thuật

Trong lĩnh vực thiết kế và mỹ thuật, hình chóp cụt mang đến những giá trị thẩm mỹ độc đáo. Các nhà thiết kế thường sử dụng hình dạng này để tạo ra những tác phẩm nghệ thuật điêu khắc ấn tượng, đèn trang trí và đồ nội thất hiện đại.

Studio thiết kế Zaha Hadid đã ứng dụng hình chóp cụt vào nhiều dự án nội thất, tạo ra những không gian sống độc đáo và sang trọng. Các tác phẩm này không chỉ đẹp mắt mà còn tối ưu được công năng sử dụng, như tủ kệ có thể tận dụng không gian theo chiều cao và góc nhìn đa chiều.

Xu hướng thiết kế minimalist hiện đại cũng ưa chuộng việc sử dụng hình chóp cụt trong các sản phẩm trang trí nội thất, từ bình hoa đến đèn trần, tạo nên những đi

Phương pháp giải các dạng bài tập về hình chóp cụt

Việc giải các bài tập hình chóp cụt đòi hỏi nắm vững kiến thức về các yếu tố hình học và công thức tính toán. Phương pháp tiếp cận cần có tính hệ thống, từ việc xác định các thành phần cơ bản đến áp dụng công thức phù hợp.

Để giải quyết hiệu quả các bài toán về hình chóp cụt, cần phân tích kỹ dữ kiện đề bài, vẽ hình minh họa chính xác và xác định rõ yếu tố cần tìm. Việc nắm vững các công thức tính diện tích, thể tích và mối quan hệ giữa các yếu tố trong hình học không gian là yếu tố then chốt.

Bài tập về tính diện tích

Khi giải bài tập tính diện tích, bước đầu tiên là xác định các thành phần cần tính như diện tích đáy, diện tích xung quanh hay diện tích toàn phần. Mỗi loại diện tích có công thức riêng và cách tiếp cận khác nhau.

Việc tính diện tích xung quanh thường liên quan đến tỷ số đồng dạng giữa hai mặt đáy và chiều cao của hình chóp cụt. Cần chú ý đến mối quan hệ giữa các cạnh bên và góc nghiêng để áp dụng công thức chính xác.

Đối với diện tích toàn phần, cần tổng hợp cả diện tích xung quanh và diện tích hai đáy. Việc kiểm tra kết quả bằng cách so sánh với các trường hợp đặc biệt giúp đảm bảo tính chính xác của lời giải.

Bài tập về tính thể tích

Thể tích hình chóp cụt được tính dựa trên diện tích hai đáy và chiều cao. Công thức cơ bản V = 1/3.h(S1 + S2 + √(S1.S2)) cần được áp dụng linh hoạt tùy theo dữ kiện đề bài.

Trong nhiều trường hợp, đề bài không cho trực tiếp các yếu tố cần thiết. Khi đó, cần vận dụng các định lý về tam giác đồng dạng hoặc quan hệ lượng giác để tìm ra các yếu tố trung gian.

Việc xác định chính xác tỷ số đồng dạng giữa hai mặt đáy là bước quan trọng, giúp tìm ra mối liên hệ giữa các kích thước tương ứng và đơn giản hóa quá trình tính toán.

Bài tập tổng hợp

Các bài tập tổng hợp thường yêu cầu kết hợp nhiều kiến thức và kỹ năng khác nhau. Việc phân tích bài toán thành các bước nhỏ giúp giải quyết vấn đề một cách có hệ thống.

Trong quá trình giải, cần chú ý đến việc chuyển đổi đơn vị đo và kiểm tra tính hợp lý của kết quả. Nhiều bài toán đòi hỏi vận dụng cả kiến thức về góc, khoảng cách và quan hệ song song, vuông góc trong không gian.

Kỹ năng vẽ hình và biểu diễn không gian ba chiều trên mặt phẳng cũng đóng vai trò quan trọng, giúp hình dung rõ ràng các yếu tố và mối quan hệ trong bài toán.

Hình chóp cụt là gì? Đây là một khái niệm quan trọng trong hình học không gian mà bạn không thể bỏ qua. Bài viết đã cung cấp đầy đủ các đặc điểm, công thức tính toán và ứng dụng thực tế của hình chóp cụt. Nắm vững kiến thức này sẽ giúp bạn tự tin hơn trong việc giải bài tập và áp dụng vào thực tế. Hãy khám phá thêm để phát triển kỹ năng toán học của mình!