Hình chóp là gì, tính chất và ứng dụng của hình chóp trong thực tế như thế nào là những lý thuyết căn bản nhưng vô cùng quan trọng trong chương trình THPT. Bài viết dưới đây của Học Thế Nào sẽ dẫn dắt bạn đi sâu vào thế giới của hình chóp trong hình học không gian, từ định nghĩa cơ bản, phân loại, tính chất, đến các công thức tính toán và ứng dụng thực tiễn của nó.
Hình chóp là gì?
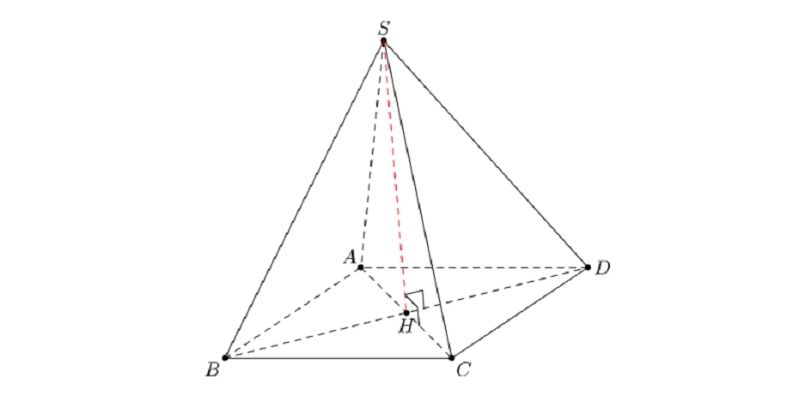
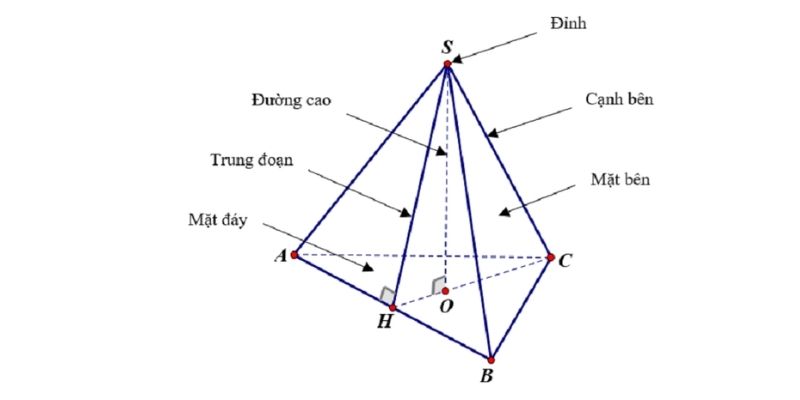
Hình chóp là một khối đa diện được tạo thành bởi một đa giác lồi (đáy) và các tam giác hội tụ tại một điểm chung được gọi là đỉnh. Các tam giác bao quanh hình chóp được gọi là mặt bên.
Có rất nhiều loại hình chóp khác nhau trong hình học không gian. Chúng được phân loại dựa theo tên đáy. Chẳng hạn như hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác, hình chóp lục giác… Ngoài ra, ta có thể phân loại hình chóp theo các tiêu chí khác như:
Theo vị trí đỉnh:
- Hình chóp đứng: Đỉnh chóp vuông góc với mặt đáy.
- Hình chóp xiên: Đỉnh chóp không vuông góc với mặt đáy.
Theo độ dài cạnh bên:
- Hình chóp đều: Các cạnh bên bằng nhau.
- Hình chóp xiên bất kỳ: Các cạnh bên không bằng nhau.
Tính chất của hình chóp
Hình chóp có những tính chất hình học như sau:
- Số cạnh, số mặt, số đỉnh:
- Số cạnh = Số cạnh đáy + Số cạnh bên
- Số mặt = Số cạnh đáy + 1
- Số đỉnh = Số mặt
- Đường cao: Đường thẳng vuông góc từ đỉnh xuống mặt đáy (chỉ xảy ra với hình chóp đứng).
- Góc chóp: Góc tạo bởi cạnh bên và mặt đáy.
- Diện tích toàn phần: Tổng diện tích các mặt của hình chóp.
- Thể tích:
- Hình chóp đứng: V = (1/3)* S*h, với S là diện tích đáy và h là chiều cao.
- Hình chóp xiên: Thể tích có thể tính bằng cách chia hình chóp thành các khối chóp con hoặc sử dụng tích phân.
Một số loại hình chóp thường gặp
Thông thường ta thường hay bắt gặp một số dạng đặc biệt của hình chóp trong các bài toán hình bao gồm: hình chóp đa giác đều, hình chóp tứ giác đều, hình chóp tam giác đều và hình chóp cụt đều.
Hình chóp đa giác đều là gì?
Hình chóp đa giác đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau. Các mặt bên của hình chóp đều là các tam giác cân bằng nhau, chung đỉnh là đỉnh của hình chóp và có chân đường cao trùng với tâm đa giác đáy.
Tính chất:
- Các cạnh bên của hình chóp đều bằng nhau.
- Các mặt bên của hình chóp đều là các tam giác cân bằng nhau.
- Các mặt bên của hình chóp đều tạo với mặt đáy các góc bằng nhau.
- Các cạnh bên của hình chóp đều tạo với mặt đáy các góc bằng nhau.
- Đường cao của hình chóp đều trùng với trục của hình chóp.
- Tâm của đa giác đáy trùng với tâm của hình chóp.
- Hình chóp đều có thể nội tiếp và ngoại tiếp một hình cầu.
Hình chóp tứ giác đều là gì?
Hình chóp tứ giác đều là hình chóp đa giác đều có đáy là hình vuông. Các mặt bên của hình chóp tứ giác đều là các tam giác cân vuông.
Ngoài các tính chất chung của hình chóp đa giác đều, hình chóp tứ giác đều còn có các tính chất sau:
- Các cạnh bên của hình chóp tứ giác đều bằng nhau và bằng đường chéo của hình vuông đáy.
- Các mặt bên của hình chóp tứ giác đều là các tam giác vuông cân có góc ở đỉnh bằng 45 độ.
- Đường cao của hình chóp tứ giác đều bằng 1/2 cạnh đáy.
- Diện tích xung quanh của hình chóp tứ giác đều bằng diện tích đáy nhân với một nửa độ dài cạnh bên.
- Thể tích của hình chóp tứ giác đều bằng 1/3 diện tích đáy nhân với chiều cao.
Hình chóp tam giác đều là gì?
Hình chóp tam giác đều là hình chóp đa giác đều có đáy là tam giác đều. Các mặt bên của hình chóp tam giác đều là các tam giác đều.
- Các cạnh bên của hình chóp tam giác đều bằng nhau và bằng đường cao của tam giác đều đáy.
- Các mặt bên của hình chóp tam giác đều là các tam giác đều có góc ở đỉnh bằng 60 độ.
- Đường cao của hình chóp tam giác đều trùng với trục của hình chóp.
- Diện tích xung quanh của hình chóp tam giác đều bằng diện tích đáy nhân với một nửa độ dài cạnh bên.
- Thể tích của hình chóp tam giác đều bằng 1/4 diện tích đáy nhân với chiều cao.
Hình chóp cụt đều là gì?
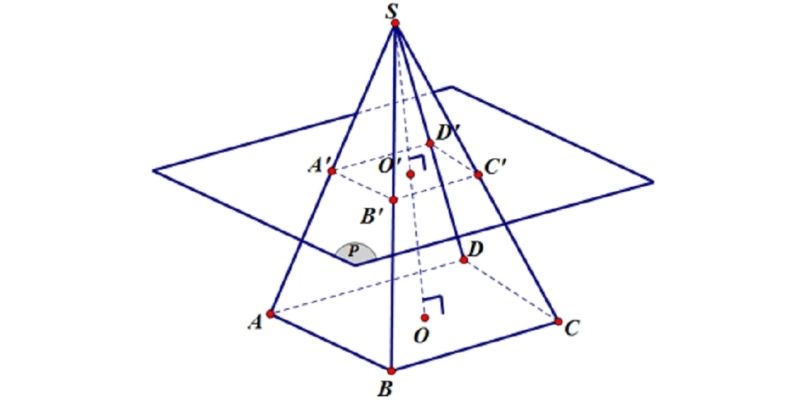
Hình chóp cụt đều là phần hình chóp đều nằm giữa mặt phẳng đáy của hình chóp và mặt phẳng song song với đáy và cắt hình chóp. Hình chóp cụt đều có hai đáy là đa giác đều song song với nhau và các mặt bên là các hình thang cân.
- Hai đáy của hình chóp cụt đều là đa giác đều đồng dạng.
- Các cạnh bên của hình chóp cụt đều bằng nhau.
- Các mặt bên của hình chóp cụt đều là các hình thang cân có các góc ở đáy bằng nhau.
- Chiều cao của hình chóp cụt đều bằng khoảng cách giữa hai đáy.
- Diện tích toàn phần của hình chóp cụt đều bằng tổng diện tích hai đáy và diện tích xung quanh.
- Thể tích của hình chóp cụt đều bằng 1/3 (S1 + S2 + √(S1 * S2)) * h, với S1 và S2 là diện tích hai đáy và h là chiều cao.
Phân biệt hình chóp có đáy là đa giác đều
Để dễ dàng phân biệt các hình chóp có đáy là đa giác đều, bạn có thể tham khảo bảng dưới đây:
| Loại hình chóp | Đáy | Mặt bên | Số cạnh đáy | Số mặt | Số cạnh |
| Hình chóp tam giác đều | Tam giác đều | Tam giác đều | 3 | 6 | 4 |
| Hình chóp tứ giác đều | Hình vuông | Tam giác cân | 4 | 8 | 5 |
| Hình chóp ngũ giác đều | Ngũ giác đều | Tam giác cân | 5 | 10 | 6 |
| Hình chóp lục giác đều | Lục giác đều | Tam giác cân | 6 | 12 | 7 |
Các công thức toán học liên quan đến hình chóp
Dưới đây là một số công thức toán học quen thuộc thường được sử dụng trong các bài tập liên quan đến hình chóp:
Công thức tính chu vi hình chóp:
Chu vi hình chóp (P) bằng tổng chu vi các mặt bên và mặt đáy:
$$ P=P_{mặt\;bên}+P_{mặt\;đáy} $$
Công thức tính diện tích xung quanh hình chóp:
Diện tích xung quanh hình chóp (Sxq) được tính bằng nửa chu vi đáy (P/2) nhân với trung đoạn (d):
$$ S_{xq}=\frac P2\times d $$
Công thức tính diện tích toàn phần hình chóp:
Diện tích toàn phẩn của hình chóp (Stp) được tính bằng tổng của diện tích xung quanh (Sxq) và diện tích đáy (Sđáy):
$$ S_{tp}=S_{xq}+S_{đáy} $$
Công thức tính thể tích hình chóp:
Thể tích hình chóp (V) được tính bằng tích của 1/2 diện tích đáy nhân với chiều cao (h):
$$ V=\frac13\times S_{đáy}\times h $$
Một số bài tập liên quan đến hình chóp
Dưới đây là một số bài tập liên quan đến các công thức cơ bản của hình chóp giúp bạn nắm vững cách giải trong phần này:
Bài tập 1:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 4cm, chiều cao của hình chóp là 3cm.
a) Tính diện tích xung quanh của hình chóp.
b) Tính thể tích của hình chóp.
Giải:
a) Diện tích xung quanh của hình chóp:
Sxq = 3 * p* a
- p: Nửa chu vi đáy (p = AB/2 = 4/2 = 2cm)
- a: Trung đoạn của một mặt bên (a = √(AB^2 – AH^2) = √(4^2 – 3^2) = √5 cm)
Sxq = 3 * 2 * √5 = 6√5 cm^2
b) Thể tích của hình chóp:
V = (1/3) * Sđáy * h
- S_đáy: Diện tích đáy (S_đáy = AB^2 = 4^2 = 16 cm^2)
- h: Chiều cao (h = 3cm)
V = (1/3) * 16 * 3 = 16 cm^3
Bài tập 2:
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 5cm, các mặt bên là tam giác cân có độ dài cạnh bên là 6cm.
a) Tính diện tích xung quanh của hình chóp.
b) Tính thể tích của hình chóp.
Giải:
a) Diện tích xung quanh của hình chóp:
Sxq = 4 * a * d
- a: Cạnh đáy hình vuông (a = 5cm)
- d: Trung đoạn của một mặt bên (d = √(AB^2 – AH^2) = √(5^2 – (6/2)^2) = √7 cm)
Sxq = 4 * 5 * √7 = 20√7 cm^2
b) Thể tích của hình chóp:
V = (1/3) * Sđáy * h
- S_đáy: Diện tích đáy (S_đáy = a^2 = 5^2 = 25 cm^2)
- h: Chiều cao (h = √(SB^2 – AB^2) = √(6^2 – 5^2) = √1 cm)
V = (1/3) * 25 * 1 = 25/3 cm^3
Bài tập 3:
Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ có các cạnh đáy ABCD và A’B’C’D’ là hình vuông cạnh 3cm, cạnh bên BB’ vuông góc với đáy dưới ABCD.
a) Tính diện tích xung quanh của hình chóp cụt.
b) Tính thể tích của hình chóp cụt.
Giải:
a) Diện tích xung quanh của hình chóp cụt:
S_xq = 1/2 * (P1 + P2) * h
- P1: Chu vi đáy dưới (P1 = 4 * a = 4 * 3 = 12cm)
- P2: Chu vi đáy trên (P2 = 4 * a’ = 4 * 3 = 12cm)
- h: Chiều cao của hình chóp cụt (h = BB’ = √(AB^2 – AA’^2) = √(3^2 – (3/2)^2) = √3/4 cm)
S_xq = 1/2 * (12 + 12) * √3/4 = 9√3 cm^2
b) Thể tích của hình chóp cụt:
V = (1/3) * h * (S1 + S2 + √(S1 * S2))
- S1: Diện tích đáy dưới (S1 = a^2 = 3^2 = 9 cm^2)
- S2: Diện tích đáy trên (S2 = a’^2 = 3^2 = 9 cm^2)
- h: Chiều cao của hình chóp cụt (h = √3/4 cm)
V = (1/3) * √3/4 * (9 + 9 + √(9 * 9))
V = (1/3) * √3/4 * (18 + 3√3)
V = (3√3 + 18√3) / 12
V = 21√3 / 12
V ≈ 3.47 cm^3
Lời kết
Hy vọng qua bài viết của chúng tôi, bạn đã nắm vững được lý thuyết về hình chóp là gì, tính chất và các công thức liên quan trong phần này. Bên cạnh đó, chúng tôi cũng đã cung cấp cho bạn một số bài tập có lời giải giúp bạn hiểu rõ hơn về cách làm những bài tập tính toán liên quan đến hình chóp. Chúc các bạn học tốt!