Tìm hiểu hình chóp tứ giác đều qua định nghĩa, tính chất và ứng dụng toán học

Hình chóp tứ giác đều là một khái niệm quan trọng trong hình học không gian, có ý nghĩa lớn trong toán học. Bài viết này sẽ cung cấp định nghĩa, tính chất, công thức và các ứng dụng của hình chóp tứ giác đều. Cùng khám phá những kiến thức thú vị và cách giải bài toán hiệu quả!

Hình chóp tứ giác đều và các đặc điểm cơ bản trong hình học không gian

Trong Hình học không gian, hình chóp tứ giác đều là một khối đa diện đặc biệt được tạo thành từ một đáy là hình vuông và 4 mặt bên là các tam giác đều bằng nhau. Đây là một trong những hình khối cơ bản và quan trọng trong không gian ba chiều.

Cấu trúc của hình chóp tứ giác đều có những đặc điểm độc đáo và thú vị. Đỉnh của hình chóp nằm trên đường thẳng vuông góc với tâm của đáy, tạo nên sự cân đối hoàn hảo. Các cạnh bên bằng nhau và các mặt bên có diện tích bằng nhau, tạo nên tính đối xứng cao.

Trong thực tế, hình dạng này xuất hiện phổ biến trong kiến trúc và thiết kế. Ví dụ điển hình là Kim tự tháp Giza ở Ai Cập – một trong những kỳ quan thế giới cổ đại được xây dựng với tỷ lệ gần như hoàn hảo của một hình chóp tứ giác đều. Các nhà khoa học đã chứng minh rằng hình dạng này mang lại sự ổn định và độ bền vượt trội cho công trình.

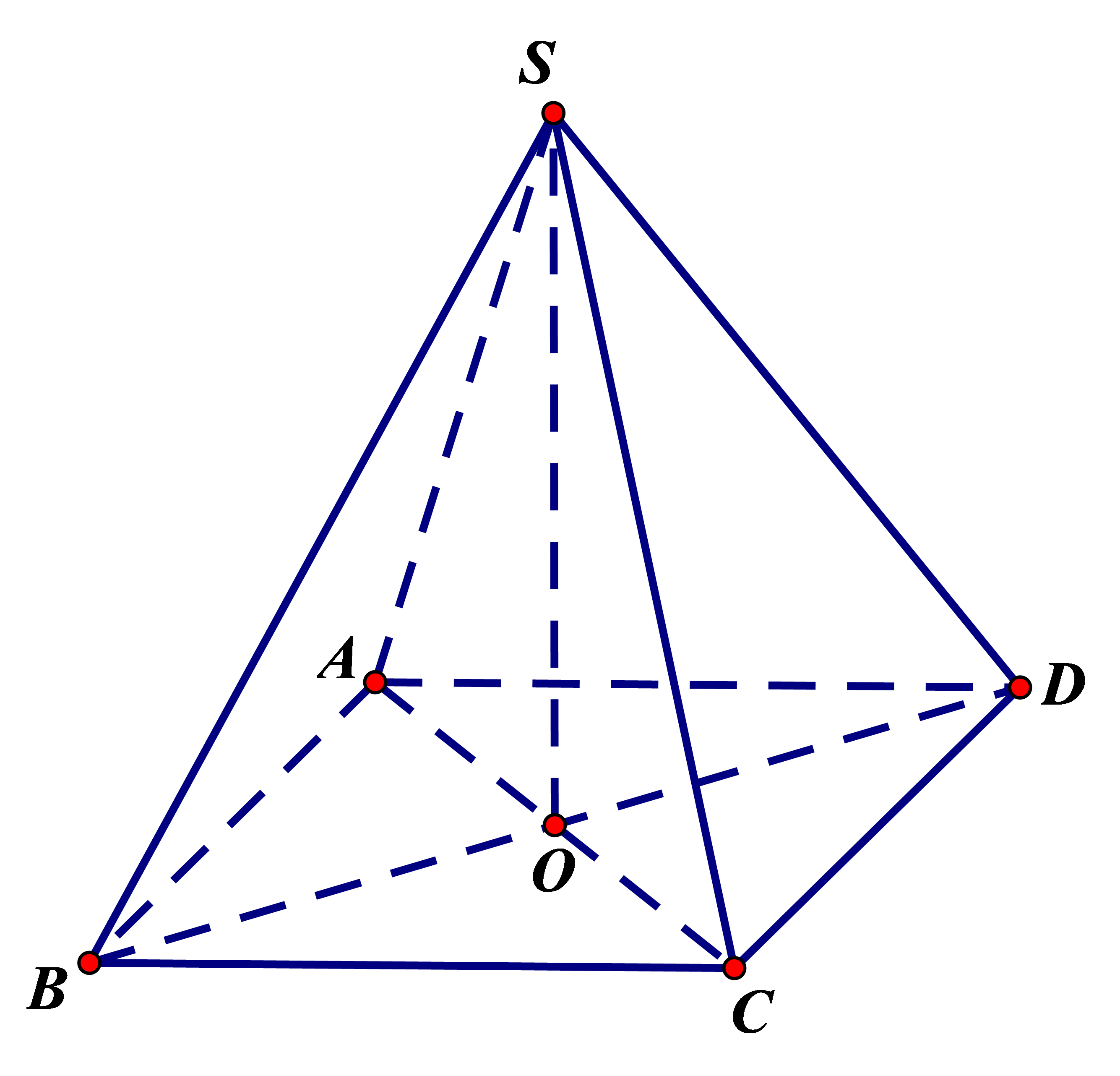
Việc hiểu rõ về hình chóp tứ giác đều không chỉ quan trọng trong toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác như kỹ thuật, xây dựng và thiết kế công nghiệp. Đặc biệt trong ngành kiến trúc, các nguyên lý của hình khối này thường được áp dụng để tạo nên những công trình vừa đẹp mắt vừa có tính ổn định cao.

Các tính chất quan trọng của hình chóp tứ giác đều trong toán học

Tính chất hình chóp tứ giác đều là những đặc điểm độc đáo giúp phân biệt nó với các hình chóp khác. Hình chóp tứ giác đều được tạo thành từ một đáy là hình vuông và một đỉnh nằm trên đường thẳng vuông góc với tâm của đáy. Các cạnh bên và mặt bên của hình này có độ dài và diện tích bằng nhau.

Đặc điểm của đáy hình chóp tứ giác đều

Đáy của hình chóp tứ giác đều là một hình vuông hoàn hảo với bốn cạnh bằng nhau và bốn góc vuông. Tương tự như hình bình hành có tâm đối xứng không​, đáy hình chóp tứ giác đều cũng có tâm đối xứng nằm tại giao điểm của hai đường chéo.

Các đường chéo của đáy cắt nhau tại tâm và chia đôi lẫn nhau. Điều này tạo nên tính đối xứng hoàn hảo cho hình chóp, giúp việc tính toán các yếu tố khác trở nên dễ dàng hơn.

Các cạnh bên và mặt bên của hình chóp tứ giác đều

Bốn cạnh bên của hình chóp tứ giác đều có độ dài bằng nhau và tạo với mặt đáy những góc bằng nhau. Điều này tạo nên sự cân đối hoàn hảo cho hình chóp. Các mặt bên là những tam giác cân đồng dạng, có diện tích bằng nhau.

Khi khai triển hình chóp, bốn mặt bên sẽ tạo thành bốn tam giác cân giống hệt nhau. Đây là một đặc điểm quan trọng giúp phân biệt hình chóp tứ giác đều với các loại hình chóp khác.

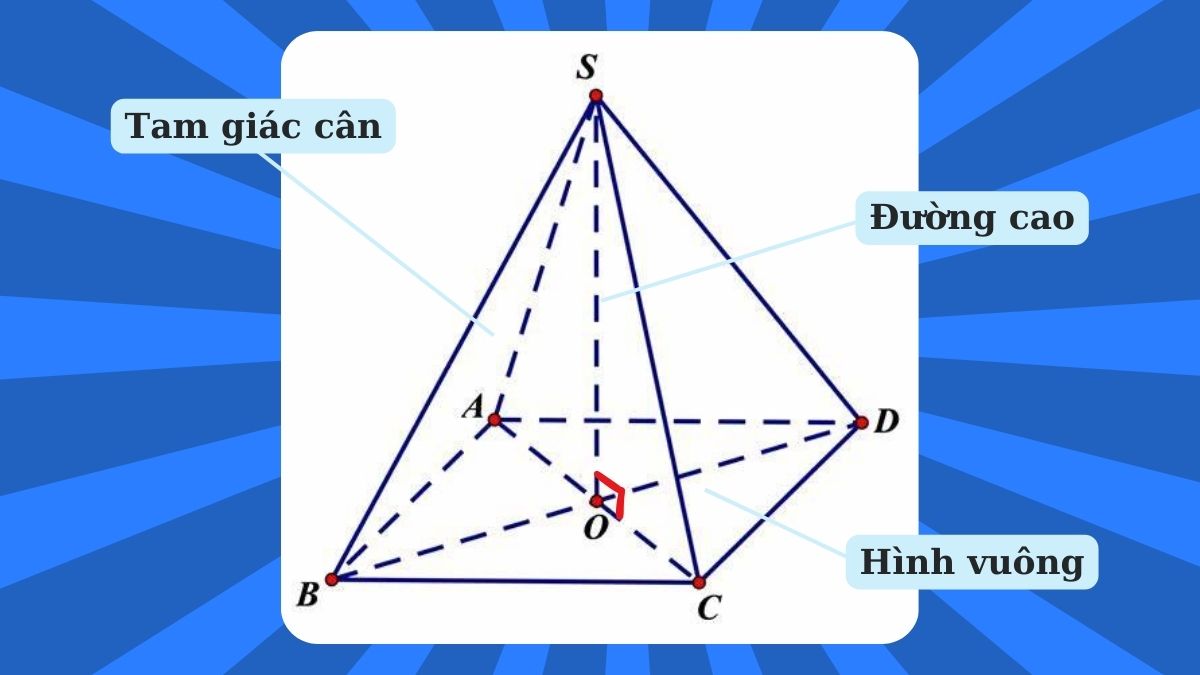
Đường cao và tâm đối xứng

Đường cao của hình chóp tứ giác đều là đoạn thẳng từ đỉnh hạ vuông góc xuống tâm của đáy. Đường cao này trùng với trục đối xứng của hình chóp, tạo nên tính đối xứng xoay bậc 4 cho hình.

Tâm đối xứng của hình chóp nằm trên đường cao, chia đường cao theo tỷ lệ 1:3 tính từ đỉnh. Vị trí này có ý nghĩa quan trọng trong việc tính toán thể tích và các yếu tố khác của hình chóp tứ giác đều.

Phương pháp tính toán các yếu tố của hình chóp tứ giác đều

Để tính toán chính xác các yếu tố của hình chóp tứ giác đều, cần nắm vững các công thức và phương pháp tính chu vi, diện tích và thể tích. Mỗi thành phần đều có mối liên hệ chặt chẽ với nhau và tuân theo các quy luật hình học không gian.

Việc tính toán các yếu tố này đòi hỏi sự hiểu biết về đặc điểm của hình chóp tứ giác đều – một khối đa diện có đáy là hình vuông và các mặt bên là những tam giác đều bằng nhau. Các phép tính cần được thực hiện theo trình tự logic từ đơn giản đến phức tạp.

Công thức tính chu vi và diện tích đáy

Chu vi đáy hình chóp tứ giác đều được tính bằng tổng độ dài 4 cạnh của hình vuông đáy. Do các cạnh bằng nhau nên chu vi bằng 4 lần độ dài một cạnh đáy.

Với diện tích đáy, ta có công thức là bình phương độ dài cạnh đáy, vì đáy là hình vuông. Công thức này áp dụng cho mọi trường hợp không phụ thuộc vào chiều cao của hình chóp.

Cách tính diện tích xung quanh và toàn phần

Diện tích hình chóp tứ giác đều xung quanh được tính bằng tổng diện tích của 4 mặt bên tam giác đều. Mỗi tam giác có diện tích bằng một nửa tích của cạnh đáy và đường cao tam giác mặt bên.

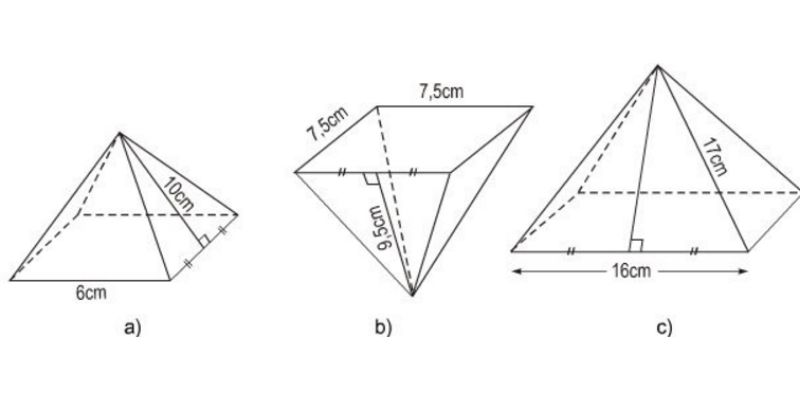
Diện tích toàn phần là tổng của diện tích xung quanh và diện tích đáy. Kết quả này cho ta biết tổng diện tích bề mặt của toàn bộ khối chóp, rất hữu ích trong các bài toán thực tế về đóng gói hay trang trí.

Công thức tính thể tích hình chóp tứ giác đều

Thể tích khối chóp tứ giác đều được tính bằng một phần ba tích của diện tích đáy và chiều cao hình chóp. Công thức thể tích hình chóp tứ giác đều này áp dụng cho mọi hình chóp có đáy là hình vuông.

Để tính chính xác, cần xác định rõ chiều cao vuông góc từ đỉnh đến mặt phẳng đáy. Chiều cao này khác với độ dài cạnh bên của hình chóp và có thể tính được thông qua định lý Pytago khi biết khoảng cách từ chân đường cao đến tâm đáy.

Hướng dẫn vẽ và xây dựng hình chóp tứ giác đều

Hình chóp tứ giác đều là gì? Đây là hình khối có đáy là hình vuông và các mặt bên là các tam giác đều bằng nhau. Đỉnh của hình chóp nằm trên đường thẳng vuông góc với tâm của đáy, tạo nên một hình khối cân đối và đẹp mắt.

Để vẽ và xây dựng hình chóp tứ giác đều cần nắm vững các nguyên tắc cơ bản về hình học không gian. Hocthenaovn cung cấp nhiều tài liệu tham khảo giúp người học dễ dàng tiếp cận kiến thức này.

Các bước vẽ hình chóp tứ giác đều cơ bản

Bước đầu tiên là vẽ hình vuông ABCD làm đáy của hình chóp. Các cạnh của hình vuông phải bằng nhau và vuông góc với nhau để tạo nên đáy chuẩn xác.

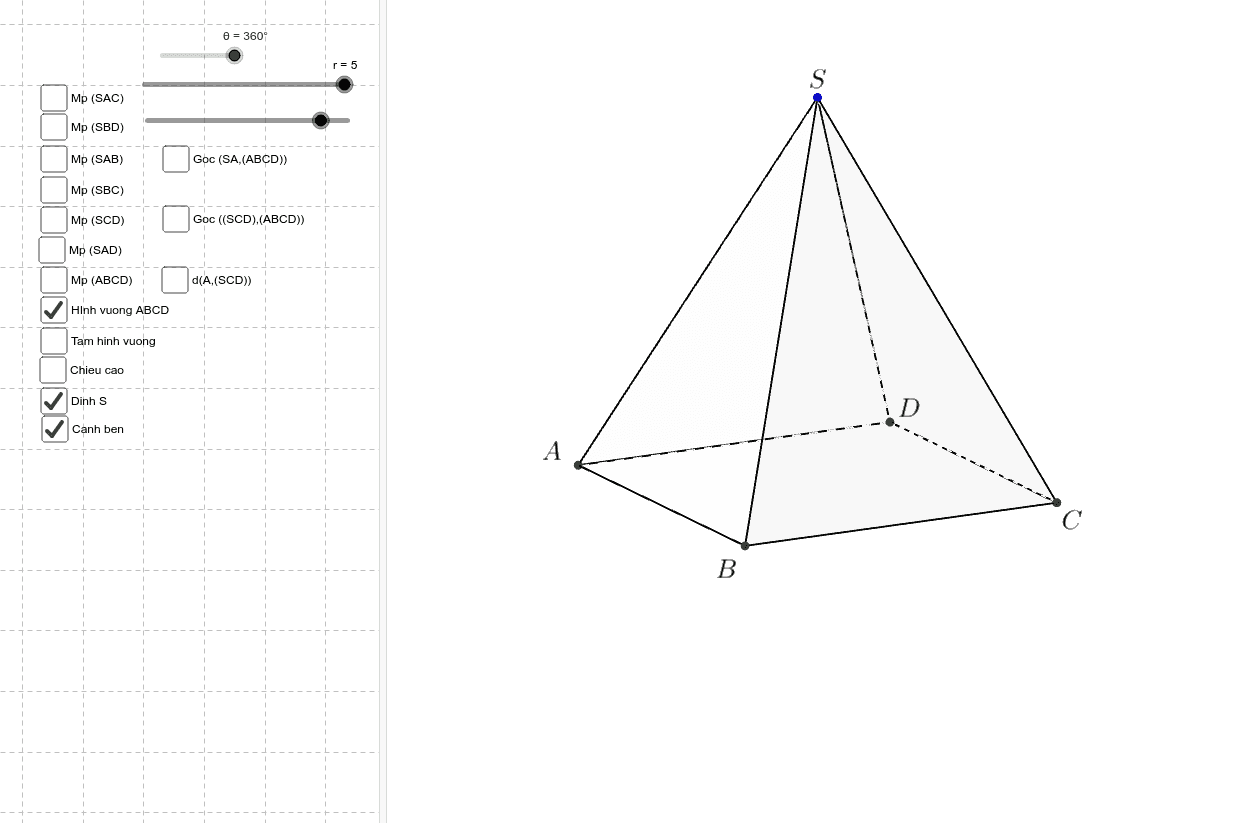
Tiếp theo, xác định tâm O của hình vuông ABCD bằng cách vẽ hai đường chéo. Từ tâm O, dựng đường thẳng vuông góc với mặt đáy và lấy một điểm S trên đường thẳng này làm đỉnh của hình chóp.

Cuối cùng, nối đỉnh S với các đỉnh A, B, C, D của đáy để hoàn thành hình chóp tứ giác đều. Các cạnh bên SA, SB, SC, SD phải bằng nhau để đảm bảo tính đều của hình chóp.

Kỹ thuật vẽ hình chiếu và thiết diện

Khi vẽ hình chiếu của hình chóp tứ giác đều, cần xác định rõ mặt phẳng chiếu và góc nhìn. Hình chiếu thẳng góc thường được sử dụng để thể hiện rõ nhất các đặc điểm của hình chóp.

Thiết diện được tạo ra khi một mặt phẳng cắt hình chóp. Để vẽ thiết diện chính xác, cần xác định đường giao của mặt phẳng cắt với các mặt của hình chóp. Các điểm giao này được nối với nhau tạo thành đường biên của thiết diện.

Việc thể hiện đường nét ẩn bằng nét đứt trong hình chiếu và thiết diện giúp người xem hiểu rõ hơn về cấu trúc không gian của hình chóp. Đồng thời, việc ghi chú kích thước và góc độ một cách rõ ràng sẽ giúp bản vẽ trở nên chuyên nghiệp và dễ hiểu hơn.

Ứng dụng và bài tập về hình chóp tứ giác đều

Ứng dụng hình chóp tứ giác đều được thể hiện rõ nét trong nhiều lĩnh vực từ kiến trúc đến công nghiệp. Trong kiến trúc, hình dạng này thường xuất hiện ở các công trình như mái nhà, tháp chuông hay các công trình tôn giáo. Trong công nghiệp, nó được ứng dụng để thiết kế các phễu chứa, bunker chứa vật liệu rời.

Để giải quyết các bài toán về hình chóp tứ giác đều, cần nắm vững các tính chất hình học cơ bản và mối quan hệ giữa các yếu tố. Việc áp dụng các định lý về tam giác vuông đồng dạng sẽ giúp giải quyết nhiều bài toán phức tạp.

Các dạng bài tập thường gặp

Trong hình học không gian, các bài tập về hình chóp tứ giác đều thường xuất hiện dưới nhiều dạng khác nhau. Phổ biến nhất là các bài toán yêu cầu tìm góc giữa các cạnh, góc giữa các mặt, hay góc giữa đường thẳng và mặt phẳng.

Một dạng bài tập khác thường xuyên xuất hiện là tìm khoảng cách giữa các đối tượng trong hình chóp. Điều này đòi hỏi việc vận dụng linh hoạt các công thức tính khoảng cách từ điểm đến đường thẳng, từ điểm đến mặt phẳng.

Phương pháp giải các bài toán về đồng dạng

Khi giải các bài toán về đồng dạng trong hình chóp tứ giác đều, việc nhận biết hai tam giác đồng dạng là bước quan trọng đầu tiên. Các tam giác được tạo bởi thiết diện song song với đáy thường đồng dạng với tam giác trong mặt đáy.

Phương pháp chiếu hình thường được sử dụng để chuyển bài toán không gian về bài toán phẳng. Điều này giúp đơn giản hóa quá trình giải và tận dụng được các tính chất của hình phẳng.

Việc sử dụng tỉ số đồng dạng cũng là một công cụ hiệu quả. Khi xác định được tỉ số đồng dạng, ta có thể dễ dàng tìm được các yếu tố còn lại của hình.

Bài tập tính toán thể tích và diện tích

Để tính toán thể tích hình chóp tứ giác đều, cần xác định chính xác diện tích đáy và chiều cao. Công thức cơ bản là một phần ba tích của diện tích đáy với chiều cao vuông góc.

Tính toán diện tích xung quanh đòi hỏi phải xác định được chiều cao hình tam giác từ đỉnh đến cạnh đáy. Diện tích toàn phần sẽ bằng tổng diện tích các mặt bên và diện tích đáy.

Trong nhiều trường hợp, việc tính toán cần kết hợp với các định lý về đường vuông góc, định lý về hình chiếu. Điều này giúp xác định chính xác các kích thước cần thiết cho bài toán.

Hình chóp tứ giác đều là một trong những khái niệm quan trọng trong hình học không gian. Việc nắm vững hình chóp tứ giác đều giúp học sinh hiểu rõ những tính chất cơ bản, công thức tính toán thể tích, diện tích, cũng như ứng dụng trong thực tế. Những kiến thức này không chỉ hỗ trợ việc giải quyết bài tập mà còn ứng dụng vào nhiều tình huống trong đời sống hàng ngày.