Hình chữ nhật có bao nhiêu tâm đối xứng và các tính chất cần biết

Hình chữ nhật có bao nhiêu tâm đối xứng? Đây là câu hỏi thú vị mà nhiều học sinh lớp 8 thường gặp. Để xác định số lượng tâm đối xứng của hình chữ nhật, bạn cần nắm rõ tính chất đặc trưng của nó. Bài viết này sẽ cung cấp phương pháp và cách giải thích chi tiết giúp bạn hiểu hơn về khái niệm này.

Hình chữ nhật có bao nhiêu tâm đối xứng?

Hình chữ nhật có 1 tâm đối xứng duy nhất, nằm tại giao điểm của hai đường chéo. Điểm này cũng chính là trung điểm của hình chữ nhật, nơi chia đôi cả chiều dài và chiều rộng của hình.

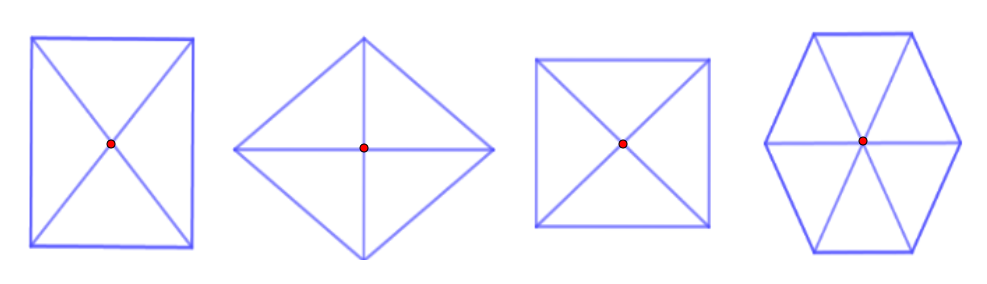
Khi xoay hình chữ nhật có bao nhiêu tâm đối xứng quanh tâm này một góc 180 độ, hình sẽ tự khớp với chính nó. Điều này chứng tỏ đây là tâm đối xứng của hình. Ngoài ra, hình chữ nhật không có tâm đối xứng nào khác vì chỉ có một điểm duy nhất thỏa mãn tính chất này.

Tâm đối xứng của hình chữ nhật cũng là điểm cân bằng của hình. Nếu đặt một tấm bìa hình chữ nhật lên đầu bút chì tại điểm này, tấm bìa sẽ nằm cân bằng hoàn hảo. Đây là một ứng dụng thực tế của việc xác định tâm đối xứng trong cuộc sống hàng ngày.

Tìm hiểu về hình chữ nhật và các tính chất cơ bản

Hình chữ nhật là một trong những hình học phẳng cơ bản và phổ biến nhất trong toán hình học phẳng. Để hiểu rõ về hình chữ nhật, cần nắm vững định nghĩa, các yếu tố cấu thành và những tính chất hình chữ nhật đặc trưng.

Định nghĩa và đặc điểm của hình chữ nhật

Hình chữ nhật là tứ giác có bốn góc vuông. Đây là một hình học phẳng đóng, có tính đối xứng cao và được ứng dụng rộng rãi trong thực tế, từ kiến trúc đến thiết kế.

Trong thực tiễn, các công trình kiến trúc nổi tiếng như tòa nhà Empire State Building tại New York được thiết kế dựa trên nguyên lý hình chữ nhật, tạo nên sự vững chắc và thẩm mỹ. Các cửa sổ, khung cửa trong nhà cũng thường có dạng hình chữ nhật để tối ưu không gian và ánh sáng.

Các yếu tố cấu thành hình chữ nhật

Một hình chữ nhật được cấu thành từ các yếu tố cơ bản sau:

• Bốn cạnh: gồm hai cặp cạnh song song và bằng nhau
• Bốn góc vuông: mỗi góc có số đo 90 độ
• Hai đường chéo: bằng nhau và cắt nhau tại trung điểm

Các yếu tố này tạo nên sự cân đối và ổn định cho hình chữ nhật. Trong thiết kế công nghiệp, các kỹ sư thường áp dụng nguyên lý này để tạo ra các sản phẩm có độ bền cao.

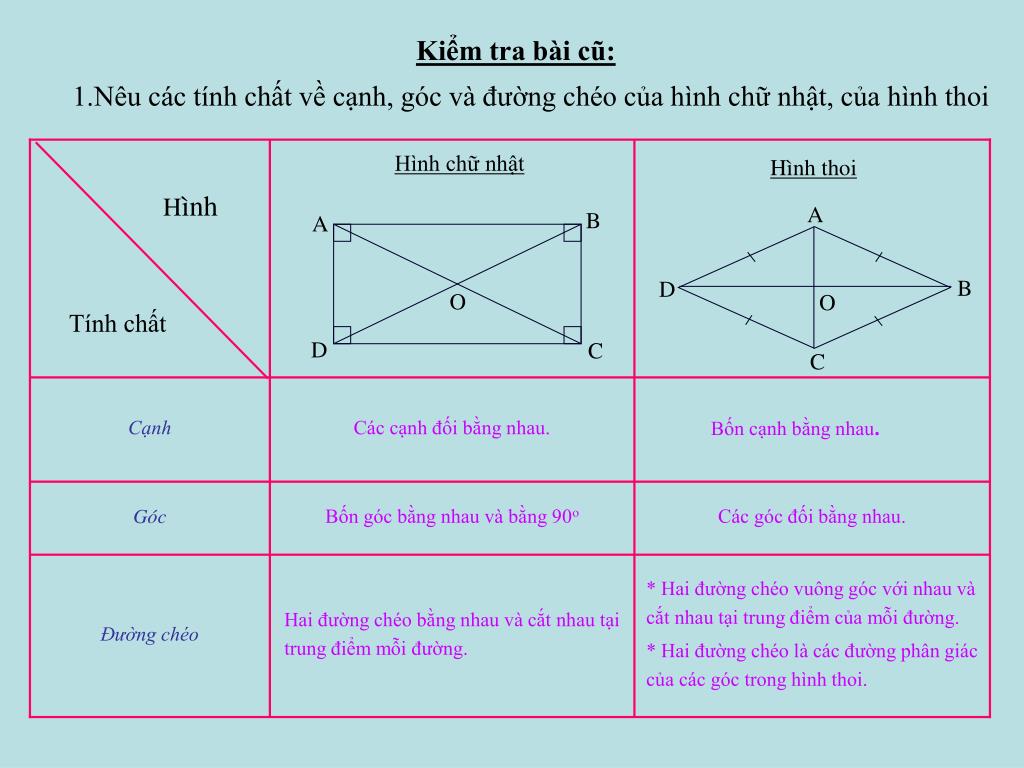
Tính chất đặc trưng của hình chữ nhật

Một hình chữ nhật có những tính chất quan trọng làm nên đặc điểm riêng biệt của nó. Các cạnh đối diện song song và bằng nhau tạo nên tính đối xứng hoàn hảo qua trục dọc và ngang.

Trong nghệ thuật và thiết kế, tỷ lệ vàng (1:1.618) thường được áp dụng để tạo ra hình chữ nhật có tính thẩm mỹ cao. Ví dụ như bức tranh Mona Lisa của Leonardo da Vinci được vẽ trong khung hình chữ nhật tuân theo tỷ lệ này.

Đặc biệt, hình chữ nhật có khả năng lát đầy mặt phẳng mà không để lại khoảng trống, tính chất này được ứng dụng rộng rãi trong thiết kế gạch lát nền, trang trí nội thất.

Phương pháp xác định tâm đối xứng trong hình chữ nhật

Việc xác định tâm đối xứng trong hình chữ nhật là một kỹ năng quan trọng trong hình học. Để tìm được tâm đối xứng chính xác, cần nắm vững các khái niệm cơ bản và quy tắc xác định. Các phương pháp xác định phương pháp xác định tâm đối xứng sẽ được trình bày chi tiết qua các phần dưới.

Khái niệm về tâm đối xứng

Tâm đối xứng là điểm mà qua đó, mỗi điểm của hình sẽ có một điểm đối xứng là gì tương ứng nằm cách đều và nằm trên cùng một đường thẳng. Khi xoay hình 180° quanh tâm đối xứng, hình sẽ trùng khớp với chính nó.

Trong hình học phẳng, tâm đối xứng có vai trò quan trọng trong việc xác định tính chất đối xứng của hình. Điểm này giúp ta hiểu rõ hơn về cấu trúc và đặc điểm của các hình hình học.

Cách xác định tâm đối xứng trong hình học phẳng

Để xác định tâm đối xứng trong hình học phẳng, ta cần dựa vào các đường chéo của hình. Đường chéo là đường thẳng nối hai đỉnh không kề nhau của hình.

Trong trường hợp hình có nhiều cạnh, việc xác định tâm đối xứng sẽ phức tạp hơn. Ta cần vẽ các đường chéo và tìm giao điểm của chúng. Giao điểm này chính là tâm đối xứng của hình.

Một cách khác là sử dụng phép quay 180° để kiểm tra. Nếu sau khi quay, hình trùng khớp với vị trí ban đầu thì điểm quay chính là tâm đối xứng.

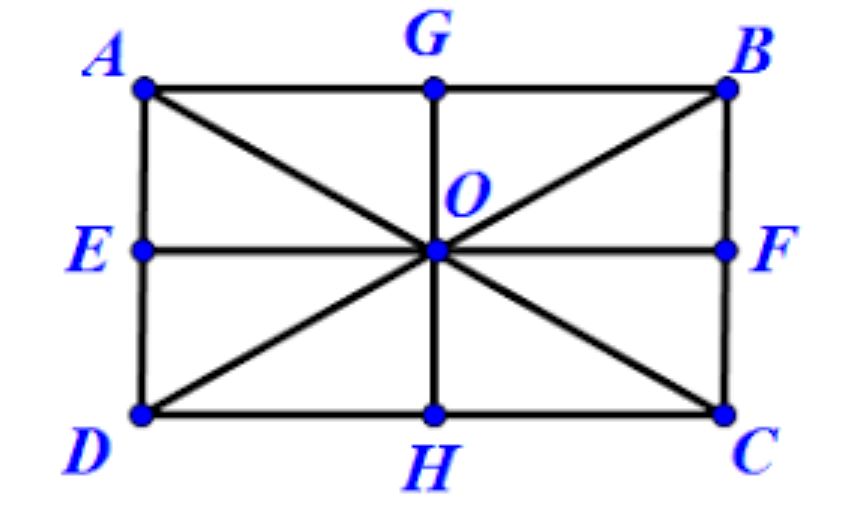
Quy tắc tìm tâm đối xứng của hình chữ nhật

Trong hình chữ nhật, tâm đối xứng nằm tại giao điểm của hai đường chéo. Điểm này cũng chính là trung điểm của mỗi đường chéo.

Để xác định chính xác, ta có thể kẻ hai đường chéo của hình chữ nhật. Hai đường này sẽ cắt nhau tại một điểm. Điểm này chia mỗi đường chéo thành hai phần bằng nhau.

Một đặc điểm quan trọng là tâm đối xứng của hình chữ nhật cũng là trung điểm của đoạn thẳng nối hai đỉnh đối diện bất kỳ. Điều này giúp ta có thêm một cách kiểm chứng độ chính xác khi xác định tâm đối xứng.

Ứng dụng tâm đối xứng trong bài tập hình chữ nhật

Tâm đối xứng là một khái niệm quan trọng trong hình học, đặc biệt khi áp dụng vào bài tập hình chữ nhật. Việc nắm vững các tính chất của tâm đối xứng giúp giải quyết nhiều dạng bài tập phức tạp một cách đơn giản và hiệu quả hơn. Như Học Thế Nào đã đề cập, việc vận dụng tâm đối xứng trong hình chữ nhật mang lại nhiều lợi ích trong học tập và thực hành toán học.

Các dạng bài tập về tâm đối xứng

Trong hình chữ nhật, tâm đối xứng thường xuất hiện dưới nhiều dạng bài tập khác nhau. Các bài toán về tính diện tích phần giao của hai hình chữ nhật là dạng phổ biến nhất, đòi hỏi học sinh phải xác định chính xác vị trí tâm đối xứng.

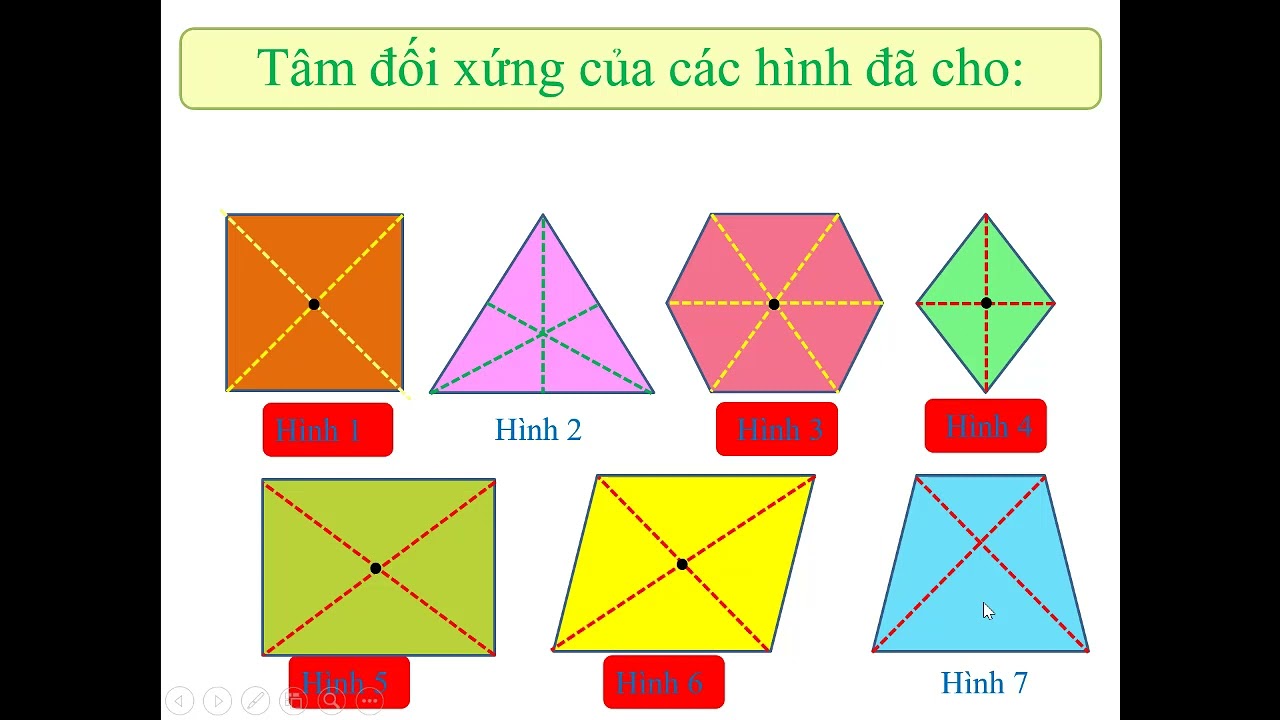
Dạng bài tập thứ hai liên quan đến việc chứng minh hai đoạn thẳng bằng nhau thông qua tâm đối xứng. Đây là dạng bài tập giúp rèn luyện kỹ năng lập luận logic và vận dụng các tính chất đối xứng.

Ngoài ra còn có các bài toán về tìm tọa độ điểm đối xứng, xác định vị trí tương đối của các đường thẳng sau khi đối xứng qua một điểm cho trước.

Phương pháp giải bài tập

Để giải các bài tập về ứng dụng tâm đối xứng, cần tuân theo quy trình giải có hệ thống. Bước đầu tiên là xác định vị trí tâm đối xứng của hình chữ nhật, thường là giao điểm của hai đường chéo.

Tiếp theo, cần vẽ các đường phụ để tạo thành các cặp điểm đối xứng. Việc này giúp nhận diện các quan hệ bằng nhau giữa các đoạn thẳng và góc.

Cuối cùng, áp dụng các tính chất của tâm đối xứng để chứng minh hoặc tính toán các yếu tố cần tìm. Đặc biệt chú ý đến tính chất: hai điểm đối xứng cách đều tâm đối xứng và nằm trên cùng một đường thẳng với tâm.

Ví dụ minh họa và hướng dẫn giải

Xét bài toán: Cho hình chữ nhật ABCD có tâm O. Điểm M nằm trên cạnh AB. Tìm điểm N trên CD sao cho MN đi qua O và ON = OM.

Cách giải:

• Xác định O là giao điểm hai đường chéo AC và BD
• Vẽ đường thẳng từ M qua O, kéo dài cắt CD tại N
• Do O là tâm đối xứng nên ON = OM

Bài toán này minh họa cách vận dụng tính chất cơ bản của tâm đối xứng để tìm điểm đối xứng. Việc nắm vững nguyên lý này sẽ giúp giải quyết nhiều bài toán phức tạp hơn một cách hiệu quả.

Mối liên hệ giữa tâm đối xứng và hình học đối xứng

Tâm đối xứng đóng vai trò then chốt trong hình học đối xứng, tạo nên sự cân bằng và hài hòa cho các hình. Điểm đặc biệt này cho phép một hình được xoay 180° quanh tâm mà vẫn trùng khớp với hình ban đầu. Ví dụ, hình chữ nhật có mấy tâm đối xứng – câu trả lời là một tâm duy nhất nằm tại giao điểm của hai đường chéo.

Tâm đối xứng tạo ra mối liên hệ chặt chẽ giữa các điểm đối xứng trên hình. Khi một điểm di chuyển, điểm đối xứng của nó cũng di chuyển theo quy luật tương ứng, duy trì tính cân đối của toàn bộ hình. Đây là nguyên lý cơ bản giúp xác định và kiểm chứng tính đối xứng của các hình học.

Vai trò của tâm đối xứng trong hình học

Tâm đối xứng giúp xác định các tính chất quan trọng của hình học. Nó là cơ sở để phân loại và nghiên cứu các dạng hình học khác nhau, từ hình cơ bản như hình lục giác đều có bao nhiêu trục đối xứng đến các hình phức tạp hơn.

Trong việc giải toán, tâm đối xứng là công cụ hữu hiệu để chứng minh các bài toán về hình học. Nó cho phép áp dụng các tính chất đối xứng để rút ngắn quá trình giải và tìm ra lời giải sáng tạo.

Tâm đối xứng còn là nền tảng để phát triển các khái niệm hình học nâng cao như phép biến hình, phép quay và phép đối xứng trục. Điều này mở rộng khả năng ứng dụng trong nhiều lĩnh vực khác nhau.

So sánh với các dạng đối xứng khác

Đối xứng tâm có những đặc điểm riêng biệt so với đối xứng trục. Trong khi đối xứng trục tạo ra hình ảnh phản chiếu qua một đường thẳng, đối xứng tâm tạo ra hình ảnh xoay 180° quanh một điểm. Điều này tạo nên sự đa dạng trong nghiên cứu hình học.

Một số hình có thể sở hữu cả tâm đối xứng và trục đối xứng như hình lập phương có mấy cạnh. Sự kết hợp này làm tăng tính đối xứng và tạo nên vẻ đẹp hoàn hảo cho hình học.

Mỗi dạng đối xứng đều có ưu điểm riêng trong việc ứng dụng thực tế. Đối xứng tâm thường được ưu tiên trong thiết kế các cấu trúc cần tính ổn định cao.

Ứng dụng trong thực tế

Trong kiến trúc, tâm đối xứng được áp dụng rộng rãi để tạo nên các công trình có tính thẩm mỹ và cân bằng. Điển hình như Taj Mahal ở Ấn Độ, với thiết kế đối xứng hoàn hảo qua tâm của tòa nhà chính.

Ngành công nghiệp sản xuất cũng tận dụng tính chất đối x

Trong bài viết, việc xác định hình chữ nhật có bao nhiêu tâm đối xứng là một nội dung quan trọng trong hình học. Hình chữ nhật không chỉ có nhiều tính chất đặc trưng mà còn cung cấp bài tập phong phú giúp học sinh rèn luyện kỹ năng. Qua việc hiểu rõ tâm đối xứng, người đọc có thể vận dụng kiến thức này vào thực tế và giải quyết các bài toán một cách hiệu quả. Việc nắm vững khái niệm này sẽ hỗ trợ các bạn trong việc tiếp cận các vấn đề hình học phức tạp hơn.