Tìm hiểu khoảng cách giữa đường thẳng và mặt phẳng trong toán học

Khoảng cách giữa đường thẳng và mặt phẳng là một khái niệm quan trọng trong hình học không gian. Các phương pháp xác định khoảng cách này bao gồm sử dụng vector pháp tuyến của mặt phẳng, hình chiếu vuông góc và công thức tính toán. Bài viết này sẽ hướng dẫn chi tiết để bạn nắm vững cách tính và ứng dụng trong thực tế.

Khoảng cách giữa đường thẳng và mặt phẳng là gì?

Khoảng cách giữa đường thẳng và mặt phẳng là độ dài đoạn thẳng ngắn nhất nối từ một điểm bất kỳ trên đường thẳng đến mặt phẳng, và đoạn thẳng này vuông góc với mặt phẳng. Đây là khoảng cách nhỏ nhất có thể đo được giữa đường thẳng và mặt phẳng.

Để xác định khoảng cách này, ta cần xét vector pháp tuyến của mặt phẳng và vector chỉ phương của đường thẳng. Khoảng cách sẽ được tính thông qua công thức toán học liên quan đến tích vô hướng của các vector này và một điểm bất kỳ trên đường thẳng.

Trong thực tế, việc tính khoảng cách giữa đường thẳng và mặt phẳng có ý nghĩa quan trọng trong nhiều lĩnh vực như kiến trúc, xây dựng và thiết kế 3D. Ví dụ, khi thiết kế cầu vượt, kỹ sư cần tính toán khoảng cách từ dầm cầu đến mặt đường bên dưới để đảm bảo độ an toàn cho các phương tiện lưu thông.

Các phương pháp xác định khoảng cách từ đường thẳng đến mặt phẳng trong không gian

Việc xác định khoảng cách đường thẳng đến mặt phẳng là một bài toán quan trọng trong hình học không gian. Có nhiều phương pháp khác nhau để giải quyết bài toán này, mỗi phương pháp đều có những ưu điểm riêng và phù hợp với từng trường hợp cụ thể. Dưới đây là 3 phương pháp chính thường được sử dụng.

Phương pháp vector pháp tuyến của mặt phẳng

Vector pháp tuyến của mặt phẳng đóng vai trò then chốt trong việc xác định khoảng cách. Phương pháp này dựa trên nguyên lý chiếu vector từ một điểm bất kỳ trên đường thẳng lên vector pháp tuyến của mặt phẳng.

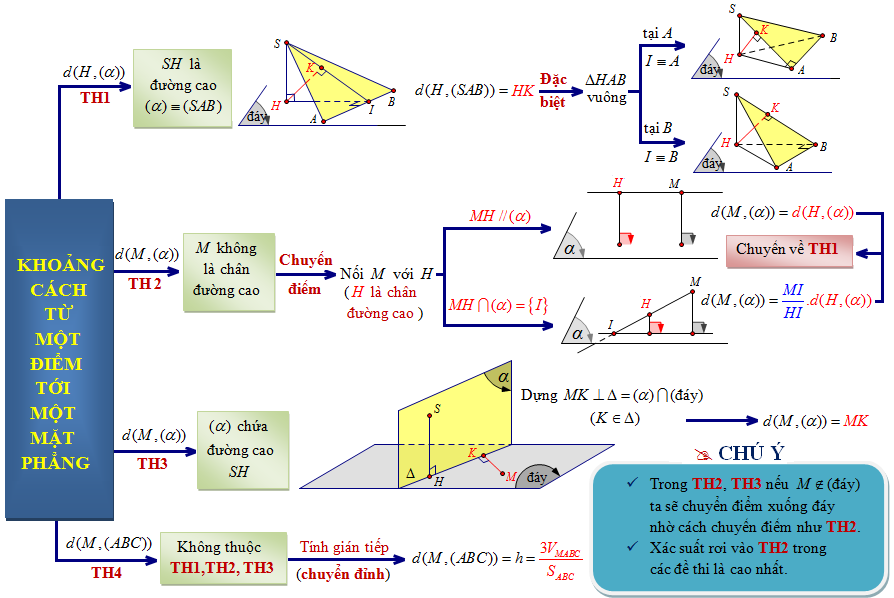
Khi áp dụng phương pháp này, ta cần xác định rõ phương trình mặt phẳng và vector pháp tuyến của nó. Sau đó, chọn một điểm bất kỳ trên đường thẳng và tính toán độ dài hình chiếu của vector nối điểm đó với một điểm trên mặt phẳng lên vector pháp tuyến.

Phương pháp hình chiếu vuông góc

Phương pháp này sử dụng tính chất của hình chiếu vuông góc để xác định khoảng cách giữa đường thẳng và mặt phẳng. Tương tự như cách tính khoảng cách từ điểm đến mặt phẳng, ta cần xác định điểm hình chiếu của một điểm trên đường thẳng xuống mặt phẳng.

Quá trình này đòi hỏi việc giải một hệ phương trình để tìm tọa độ điểm hình chiếu. Sau khi có được điểm hình chiếu, khoảng cách cần tìm chính là độ dài đoạn thẳng nối điểm ban đầu với điểm hình chiếu của nó.

Phương pháp sử dụng công thức tính khoảng cách

Phương pháp này áp dụng trực tiếp công thức tính khoảng cách giữa đường thẳng và mặt phẳng. Công thức này được xây dựng dựa trên các yếu tố hình học và đại số tuyến tính.

Ưu điểm của phương pháp này là tính nhanh chóng và chính xác. Tuy nhiên, người sử dụng cần nắm vững cách áp dụng công thức và các điều kiện cần thiết để đảm bảo kết quả chính xác.

Việc áp dụng công thức đòi hỏi ta phải biết được phương trình tham số của đường thẳng và phương trình tổng quát của mặt phẳng. Từ đó, thay các hệ số vào công thức để tính ra kết quả cuối cùng.

Công thức tính khoảng cách giữa đường thẳng và mặt phẳng song song

Khoảng cách giữa đường thẳng và mặt phẳng được xác định bằng công thức d = |ax0 + by0 + cz0 + d|/√(a² + b² + c²), trong đó (x0, y0, z0) là một điểm bất kỳ trên đường thẳng và ax + by + cz + d = 0 là phương trình mặt phẳng. Công thức này áp dụng cho cả trường hợp đường thẳng song song hoặc cắt mặt phẳng.

Để áp dụng công thức chính xác, cần xác định rõ vị trí tương đối giữa đường thẳng và mặt phẳng. Học thế nào sẽ giúp bạn hiểu rõ hơn về cách áp dụng công thức trong từng trường hợp cụ thể.

Trường hợp đường thẳng và mặt phẳng song song

Khi đường thẳng song song với mặt phẳng, khoảng cách giữa chúng sẽ không đổi tại mọi điểm. Vector chỉ phương của đường thẳng vuông góc với vector pháp tuyến của mặt phẳng.

Để xác định khoảng cách trong trường hợp này, ta chỉ cần lấy một điểm bất kỳ trên đường thẳng và thay vào công thức. Kết quả tính được sẽ là khoảng cách ngắn nhất giữa đường thẳng và mặt phẳng.

Trường hợp đường thẳng và mặt phẳng cắt nhau

Khi đường thẳng cắt mặt phẳng, khoảng cách giữa chúng bằng 0 tại điểm cắt. Vector chỉ phương của đường thẳng không vuông góc với vector pháp tuyến của mặt phẳng.

Trong thực tế, việc xác định điểm cắt giữa đường thẳng và mặt phẳng có ý nghĩa quan trọng trong nhiều ứng dụng như thiết kế 3D, xây dựng và kiến trúc.

Ứng dụng công thức trong các bài toán thực tế

Trong lĩnh vực xây dựng, công thức này được sử dụng để tính khoảng cách an toàn giữa các cấu trúc. Ví dụ, khi thiết kế đường ống dẫn gas đi qua các tòa nhà, kỹ sư cần đảm bảo khoảng cách tối thiểu để tránh rủi ro.

Trong ngành hàng không, việc tính toán khoảng cách giữa đường bay của máy bay và các chướng ngại vật như núi cao hay công trình xây dựng là yếu tố quan trọng đảm bảo an toàn bay.

Các phần mềm thiết kế 3D như AutoCAD và SketchUp cũng ứng dụng công thức này để tính toán và hiển thị chính xác vị trí các đối tượng trong không gian ba chiều.

Phương pháp giải các dạng bài tập về khoảng cách giữa đường và mặt

Để tính khoảng cách giữa đường thẳng và mặt phẳng, cần xác định vector pháp tuyến của mặt phẳng và vector chỉ phương của đường thẳng. Phương pháp này giúp tìm được khoảng cách ngắn nhất giữa hai đối tượng hình học trong không gian.

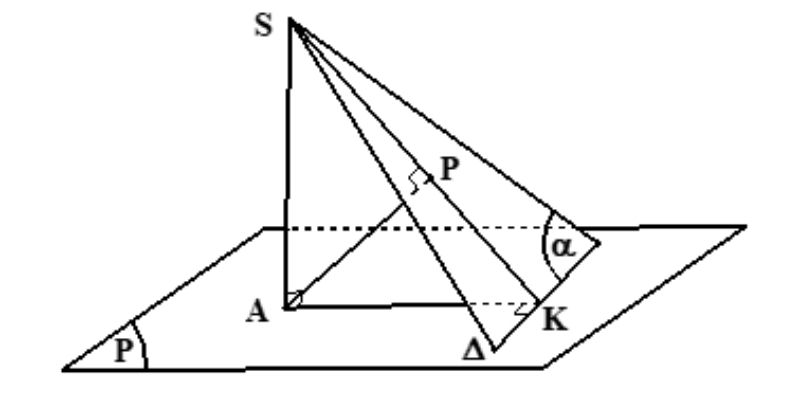
Việc tính khoảng cách giữa đường và mặt đòi hỏi sự kết hợp giữa kiến thức về vector và phép chiếu vuông góc. Tương tự như khoảng cách giữa 2 đường thẳng, ta cần xác định điểm chung và góc giữa hai đối tượng.

Bài tập mẫu và phương pháp giải

Khi giải bài tập về khoảng cách, bước đầu tiên là xác định phương trình của đường thẳng và mặt phẳng. Sau đó, tính vector pháp tuyến của mặt phẳng và vector chỉ phương của đường thẳng.

Tiếp theo, áp dụng công thức tính khoảng cách bằng cách lấy tích vô hướng của vector pháp tuyến đơn vị với vector nối một điểm bất kỳ trên đường thẳng đến một điểm bất kỳ trên mặt phẳng.

Cuối cùng, lấy giá trị tuyệt đối của kết quả để được khoảng cách cần tìm. Phương pháp này áp dụng cho mọi trường hợp, kể cả khi đường thẳng song song hoặc cắt mặt phẳng.

Các dạng bài tập thường gặp

Dạng 1: Tính khoảng cách khi đường thẳng song song với mặt phẳng. Trường hợp này đơn giản nhất vì khoảng cách không đổi tại mọi điểm.

Dạng 2: Xác định khoảng cách khi đường thẳng cắt mặt phẳng. Khi này khoảng cách bằng 0 và cần tìm tọa độ giao điểm.

Dạng 3: Tìm khoảng cách khi đường thẳng và mặt phẳng chéo nhau. Đây là dạng phức tạp nhất, đòi hỏi áp dụng đầy đủ các bước tính toán.

Lưu ý khi giải bài tập

Cần kiểm tra kỹ mối quan hệ giữa đường thẳng và mặt phẳng trước khi áp dụng công thức. Việc này giúp tránh sai sót và chọn phương pháp giải phù hợp.

Khi tính toán vector pháp tuyến và vector chỉ phương, phải đảm bảo các vector được chuẩn hóa. Điều này ảnh hưởng trực tiếp đến độ chính xác của kết quả cuối cùng.

Với các bài tập phức tạp, nên vẽ hình minh họa để hình dung rõ vị trí tương đối giữa đường thẳng và mặt phẳng. Phương pháp này giúp kiểm tra tính hợp lý của kết quả tính được.

Ứng dụng của khoảng cách giữa đường thẳng và mặt phẳng trong thực tế

Việc tính khoảng cách giữa đường thẳng và mặt phẳng có nhiều ứng dụng quan trọng trong đời sống và sản xuất. Kiến thức này giúp các kỹ sư, kiến trúc sư và nhà thiết kế tối ưu hóa không gian, đảm bảo an toàn và tính thẩm mỹ cho các công trình.

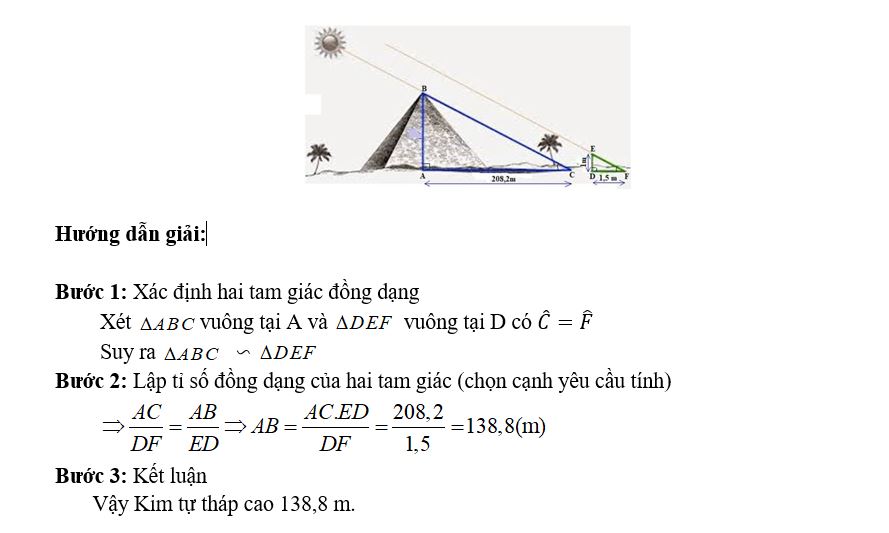
Để áp dụng hiệu quả, các chuyên gia thường sử dụng cách tính khoảng cách từ đường thẳng đến mặt phẳng thông qua các phần mềm chuyên dụng, kết hợp với kinh nghiệm thực tế để đưa ra những giải pháp tối ưu nhất.

Ứng dụng trong kiến trúc và xây dựng

Trong lĩnh vực kiến trúc, việc tính toán khoảng cách giữa các đường ống kỹ thuật và sàn nhà đóng vai trò quan trọng. Theo tiêu chuẩn của Hiệp hội Kỹ sư Cơ khí Hoa Kỳ (ASME), khoảng cách tối thiểu giữa đường ống và mặt sàn phải đảm bảo để thuận tiện cho việc bảo trì và sửa chữa.

Các công trình cầu đường cũng áp dụng nguyên lý này để thiết kế khoảng cách an toàn giữa dây văng và mặt cầu. Ví dụ như cầu Nhật Tân ở Hà Nội, các kỹ sư đã tính toán kỹ lưỡng khoảng cách này để đảm bảo độ võng cho phép và tuổi thọ công trình.

Ứng dụng trong thiết kế và công nghiệp

Ngành công nghiệp ô tô sử dụng các tính toán khoảng cách trong thiết kế hệ thống treo. Hãng Mercedes-Benz áp dụng công nghệ AIRMATIC cho phép điều chỉnh khoảng cách giữa gầm xe và mặt đường, tối ưu hóa khí động học và mang lại cảm giác lái thoải mái.

Trong sản xuất robot công nghiệp, việc tính toán chính xác khoảng cách giữa cánh tay robot và bề mặt làm việc giúp tăng độ chính xác và hiệu quả sản xuất. Công ty FANUC đã phát triển hệ thống cảm biến thông minh, cho phép robot tự động điều chỉnh khoảng cách này với độ chính xác đến micromet.

Ứng dụng trong các lĩnh vực khác

Trong ngành hàng không, khoảng cách giữa các đường bay và bề mặt địa hình được tính toán kỹ lưỡng để đảm bảo an toàn. Tổ chức Hàng không Dân dụng Quốc tế (ICAO) quy định các tiêu chuẩn nghiêm ngặt về độ cao tối thiểu giữa đường bay và địa hình.

Lĩnh vực y tế ứng dụng các tính toán khoảng cách trong phẫu thuật robot, nơi các cánh tay robot cần di chuyển chính xác theo quỹ đạo định sẵn. Hệ thống phẫu thuật Da Vinci sử dụng công nghệ định vị 3D để duy trì khoảng cách tối ưu giữa dụng cụ phẫu thuật và các mô.

Ngành điện lực áp dụng nguyên lý này trong việc thiết kế đường dây tải điện, tính toán khoảng cách an toàn giữa dây đi

Trong toán học, khoảng cách giữa đường thẳng và mặt phẳng là một khái niệm quan trọng, giúp chúng ta hiểu rõ hơn về vị trí trong không gian. Bài viết đã trình bày các phương pháp xác định khoảng cách này cùng với công thức tính toán cụ thể. Hiểu biết về khoảng cách sẽ hỗ trợ hiệu quả trong việc giải quyết các bài tập liên quan và ứng dụng trong thực tiễn, đặc biệt trong lĩnh vực kiến trúc và thiết kế.