Hướng dẫn viết phương trình mặt phẳng đi qua 3 điểm trong không gian Oxyz

Phương trình mặt phẳng đi qua 3 điểm là một khái niệm quan trọng trong hình học không gian. Việc xác định mặt phẳng này không chỉ yêu cầu bạn hiểu rõ cách viết phương trình mà còn cần tìm hiểu các ứng dụng thực tế trong giải toán. Bài viết này sẽ cung cấp cho bạn các phương pháp, công thức và ví dụ cụ thể để dễ dàng thao tác với bài toán liên quan đến mặt phẳng trong không gian.

Phương trình mặt phẳng đi qua 3 điểm và cách xác định trong không gian Oxyz

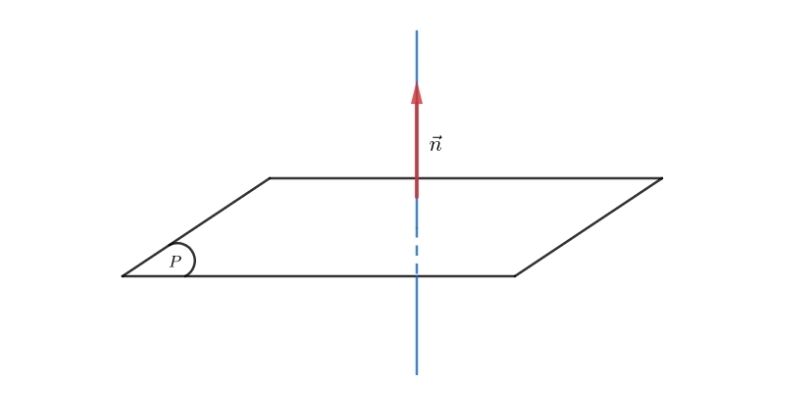
Trong hình học không gian oxyz, phương trình mặt phẳng đi qua 3 điểm là một dạng phương trình quan trọng giúp xác định vị trí và hướng của mặt phẳng. Để xác định phương trình này, ta cần có tọa độ của 3 điểm không thẳng hàng làm cơ sở.

Khi có 3 điểm A(x₁,y₁,z₁), B(x₂,y₂,z₂), C(x₃,y₃,z₃) không thẳng hàng, ta có thể xác định phương trình mặt phẳng bằng cách sử dụng định thức. Phương trình tổng quát có dạng:

|x-x₁ y-y₁ z-z₁|
|x₂-x₁ y₂-y₁ z₂-z₁| = 0
|x₃-x₁ y₃-y₁ z₃-z₁|

Việc triển khai định thức này sẽ cho ta phương trình dạng ax + by + cz + d = 0, trong đó a, b, c là các hệ số và d là số hạng tự do. Các hệ số này được tính từ tọa độ của 3 điểm đã cho và thể hiện vector pháp tuyến của mặt phẳng. Phương pháp này đảm bảo tính chính xác và hiệu quả trong việc xác định phương trình mặt phẳng trong không gian ba chiều.

Các phương pháp viết phương trình mặt phẳng đi qua 3 điểm không thẳng hàng

Để viết phương trình mặt phẳng đi qua 3 điểm, chúng ta cần xác định được vector pháp tuyến của mặt phẳng và một điểm thuộc mặt phẳng đó. Có nhiều phương pháp khác nhau để thực hiện việc này, mỗi phương pháp đều có những ưu điểm riêng tùy thuộc vào bài toán cụ thể.

Khi ba điểm không thẳng hàng cho trước, chúng sẽ xác định duy nhất một mặt phẳng trong không gian. Điều này là do ba điểm không thẳng hàng tạo thành một tam giác, và tam giác này nằm trên mặt phẳng cần tìm. Để vecto đồng phẳng là gì giúp xác định mặt phẳng một cách chính xác.

Phương pháp sử dụng định thức

Phương pháp sử dụng định thức là cách tiếp cận phổ biến để viết pt mặt phẳng đi qua 3 điểm. Phương pháp này dựa trên việc biểu diễn điều kiện đồng phẳng của bốn điểm thông qua định thức.

Khi có ba điểm A(x₁,y₁,z₁), B(x₂,y₂,z₂), C(x₃,y₃,z₃), ta sẽ xét một điểm bất kỳ M(x,y,z) thuộc mặt phẳng. Điều kiện để bốn điểm A, B, C, M đồng phẳng được biểu diễn qua định thức bằng 0.

Ưu điểm của phương pháp này là tính toán khá đơn giản và có thể áp dụng cho mọi trường hợp ba điểm không thẳng hàng.

Phương pháp sử dụng vector pháp tuyến

Vector pháp tuyến của mặt phẳng có thể được tìm bằng cách lấy tích có hướng của hai vector chỉ phương nằm trên mặt phẳng. Đây là phương pháp hiệu quả để viết ptmp đi qua 3 điểm.

Từ ba điểm A, B, C cho trước, ta xác định hai vector AB và AC. Tích có hướng của AB và AC sẽ cho ta vector pháp tuyến của mặt phẳng.

Phương pháp này đặc biệt hữu ích khi cần tìm góc giữa hai mặt phẳng hoặc khoảng cách từ một điểm đến mặt phẳng.

Phương pháp tham số hóa

Phương pháp tham số hóa sử dụng hai tham số để biểu diễn mọi điểm trên mặt phẳng. Điểm bất kỳ trên mặt phẳng được biểu diễn dưới dạng tổ hợp tuyến tính của ba điểm cho trước.

Phương trình tham số của mặt phẳng có dạng: M = A + u(B-A) + v(C-A), trong đó u và v là các tham số. Từ phương trình tham số, ta có thể chuyển về phương trình tổng quát của mặt phẳng.

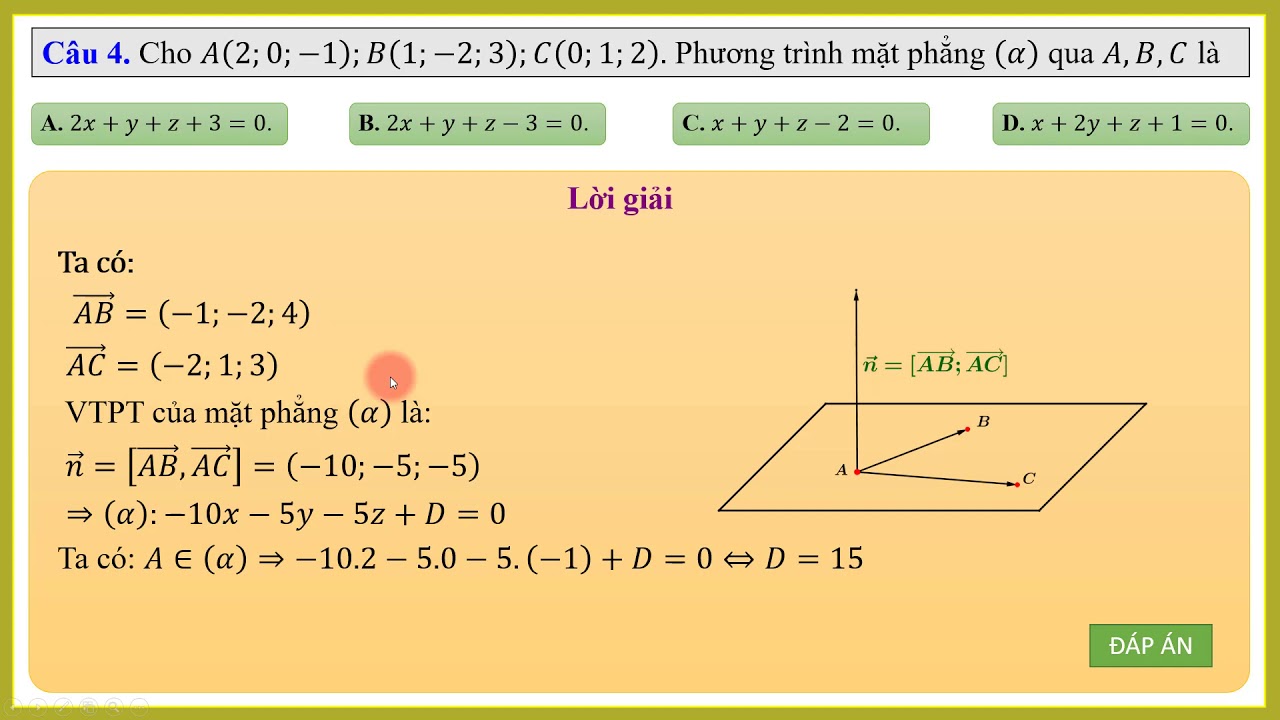
Phương pháp này rất thuận lợi khi cần xét các bài toán về giao tuyến của hai mặt phẳng hoặc tìm tập hợp điểm thỏa mãn các điều kiện phức tạp.

Công thức tổng quát và các dạng phương trình mặt phẳng trong không gian

Mặt phẳng trong không gian có thể được biểu diễn bằng nhiều dạng phương trình khác nhau. Mỗi dạng phương trình có những ưu điểm riêng và phù hợp với từng bài toán cụ thể. Phương trình mặt phẳng qua 3 điểm là một trong những dạng cơ bản và thường gặp nhất.

Để xác định một mặt phẳng trong không gian, ta cần biết các yếu tố xác định như vector pháp tuyến, điểm thuộc mặt phẳng hoặc ba điểm không thẳng hàng. Từ đó có thể viết được công thức mặt phẳng phù hợp với bài toán.

Phương trình tổng quát Ax + By + Cz + D = 0

Phương trình tổng quát là dạng phổ biến nhất để biểu diễn mặt phẳng trong không gian. Vector pháp tuyến của mặt phẳng có tọa độ n(A,B,C) vuông góc với mọi vector nằm trong mặt phẳng.

Hệ số A, B, C không đồng thời bằng 0 và D là hằng số. Khi biết tọa độ một điểm M0(x0,y0,z0) thuộc mặt phẳng, ta có thể tìm được D = -(Ax0 + By0 + Cz0).

Phương trình tham số của mặt phẳng

Phương trình tham số thể hiện mối quan hệ giữa tọa độ điểm bất kỳ trên mặt phẳng với hai tham số t và s. Dạng này đặc biệt hữu ích khi nghiên cứu các bài toán về tập hợp điểm.

Nếu biết một điểm M0(x0,y0,z0) và hai vector a(a1,a2,a3), b(b1,b2,b3) không cùng phương nằm trong mặt phẳng, ta có thể viết mặt phẳng trung trực dưới dạng tham số.

Phương trình pháp tuyến của mặt phẳng

Phương trình pháp tuyến được xây dựng dựa trên tính chất vector pháp tuyến vuông góc với mọi vector nằm trong mặt phẳng. Dạng này thường được sử dụng khi đã biết một điểm và vector pháp tuyến của mặt phẳng.

Vector pháp tuyến n(A,B,C) và một điểm M0(x0,y0,z0) thuộc mặt phẳng cho phép ta viết phương trình pháp tuyến dưới dạng: A(x-x0) + B(y-y0) + C(z-z0) = 0. Đây là dạng phương trình rất thuận tiện khi giải các bài toán về góc giữa hai mặt phẳng.

Ứng dụng của phương trình mặt phẳng trong giải toán hình học không gian

Phương trình mặt phẳng là công cụ quan trọng giúp giải quyết nhiều bài toán hình học không gian. Việc tìm phương trình mặt phẳng giúp xác định chính xác vị trí và hướng của mặt phẳng trong không gian ba chiều. Để áp dụng hiệu quả, ta cần nắm vững các ứng dụng cơ bản sau.

Xác định vị trí tương đối của điểm và mặt phẳng

Khi thay tọa độ một điểm vào phương trình mặt phẳng, ta có thể xác định được vị trí tương đối giữa điểm và mặt phẳng. Nếu kết quả bằng 0, điểm đó nằm trên mặt phẳng. Như vậy, để xác định một điểm trên mặt phẳng, ta chỉ cần kiểm tra điều kiện này.

Trong thực tế, phương pháp này được Hocthenao ứng dụng rộng rãi trong thiết kế 3D và xây dựng. Các kỹ sư thường sử dụng để kiểm tra độ phẳng của các bề mặt công trình hoặc xác định vị trí các điểm neo trong không gian.

Tính khoảng cách từ điểm đến mặt phẳng

Công thức tính khoảng cách từ điểm đến mặt phẳng là một trong những ứng dụng phương trình mặt phẳng phổ biến nhất. Khoảng cách này được tính bằng giá trị tuyệt đối của tử số chia cho mẫu số trong công thức.

Trong ngành xây dựng, công thức này giúp tính toán độ lệch của các cấu kiện so với mặt phẳng chuẩn. Các chuyên gia kiểm định chất lượng sử dụng kết quả để đánh giá độ chính xác trong thi công.

Tìm giao tuyến của hai mặt phẳng

Giao tuyến của hai mặt phẳng là một đường thẳng được xác định bằng cách giải hệ phương trình của hai mặt phẳng đó. Phương pháp này đặc biệt quan trọng trong thiết kế kiến trúc và xây dựng.

Trong công nghiệp sản xuất, việc xác định giao tuyến giúp tính toán chính xác đường cắt giữa các tấm panel hoặc vị trí hàn nối các tấm kim loại. Nhiều phần mềm CAD hiện đại đã tích hợp tính năng này để hỗ trợ người dùng thiết kế nhanh chóng và chính xác.

Bài tập và phương pháp giải các dạng toán về mặt phẳng đi qua 3 điểm

Việc xác định mặt phẳng đi qua 3 điểm là một bài toán quan trọng trong hình học không gian. Phương pháp giải các dạng toán này thường dựa vào việc thiết lập phương trình mặt phẳng và kiểm tra các điều kiện đã cho.

Để giải quyết các bài toán về mặt phẳng trong không gian, cần nắm vững các kiến thức về vector pháp tuyến và phương trình tổng quát của mặt phẳng. Việc phương trình bậc 3 có 3 nghiệm khi nào cũng có mối liên hệ chặt chẽ với bài toán này khi xét về mặt đại số.

Bài tập mẫu có lời giải chi tiết

Bài toán: Cho 3 điểm A(1,2,3), B(2,1,4), C(3,2,1). Tìm phương trình tính diện tích mặt phẳng đi qua 3 điểm đó.

Bước 1: Xác định vector pháp tuyến của mặt phẳng bằng tích có hướng của hai vector AB và AC.
Bước 2: Thay tọa độ điểm A vào phương trình tổng quát ax + by + cz + d = 0.
Bước 3: Giải hệ phương trình để tìm các hệ số.

Các dạng bài tập thường gặp

Các bài toán về mặt phẳng thường xuất hiện dưới nhiều dạng khác nhau. điều kiện để pt bậc 3 có 3 nghiệm có thể áp dụng trong một số trường hợp đặc biệt.

Một số dạng bài tập phổ biến bao gồm tìm phương trình mặt phẳng, xác định góc giữa hai mặt phẳng và tính khoảng cách từ điểm đến mặt phẳng. pt có 3 nghiệm pb khi nào là một công cụ hữu ích để kiểm tra tính đúng đắn của kết quả.

Phương pháp kiểm tra kết quả

Để kiểm tra kết quả bài toán mặt phẳng, có thể áp dụng nhiều phương pháp khác nhau. Việc viet hàm bậc 3 và kiểm tra các điều kiện đặc biệt là một cách tiếp cận hiệu quả.

Phương pháp thế tọa độ các điểm vào phương trình mặt phẳng tìm được là cách kiểm tra phổ biến nhất. Nếu kết quả đúng, tọa độ của cả ba điểm phải thỏa mãn phương trình.

Ngoài ra, có thể kiểm tra bằng cách tính góc giữa vector pháp tuyến của mặt phẳng với các vector tạo bởi ba điểm đã cho. Các góc này phải vuông góc với nhau nếu kết quả chính xác.

Phương trình mặt phẳng đi qua 3 điểm là một khái niệm cơ bản trong hình học không gian. Việc xác định và viết phương trình mặt phẳng này không chỉ giúp bạn hiểu rõ hơn về cấu trúc hình học mà còn ứng dụng được trong nhiều bài tập môn toán. Hãy cùng khám phá và thực hành để nắm vững kiến thức này, từ đó nâng cao kỹ năng giải toán và ứng dụng trong thực tiễn.