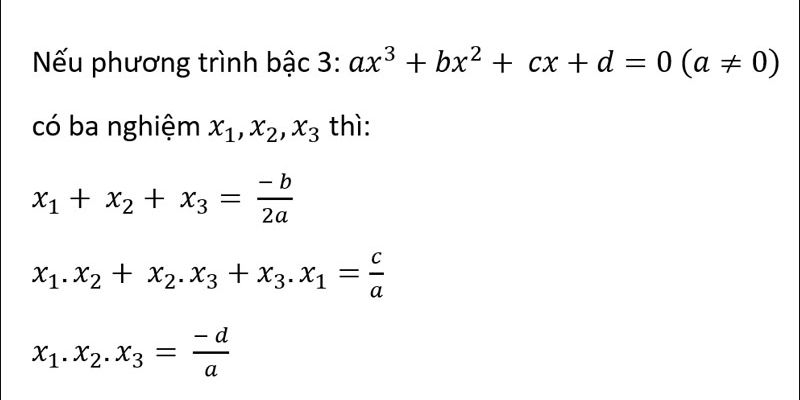Phương trình bậc 3: Cách giải và tính toán nghiệm hiệu quả trong toán học

Phương trình bậc 3: Kiến thức và ứng dụng trong toán học Phương trình bậc 3 là một phần quan trọng trong chương trình toán học. Bài viết này cung cấp kiến thức về công thức, phương pháp giải và các dạng bài tập thường gặp. Bạn sẽ tìm thấy hướng dẫn cụ thể giúp nắm vững cách giải quyết các bài toán liên quan đến loại phương trình này một cách hiệu quả.

Phương trình bậc 3 và các dạng tổng quát trong toán học

Phương trình bậc 3 là phương trình đại số có dạng tổng quát ax³ + bx² + cx + d = 0, trong đó a ≠ 0 và a, b, c, d là các hệ số thực. Đây là dạng phương trình phức tạp hơn so với phương trình bậc nhất một ẩn có dạng và thường xuất hiện trong nhiều bài toán thực tế.

Trong toán học, phương trình bậc ba có thể được giải bằng nhiều phương pháp khác nhau như công thức Cardano, phương pháp thế, phương pháp đổi biến hoặc phương pháp đồ thị. Mỗi phương pháp đều có những ưu điểm và hạn chế riêng, tùy thuộc vào dạng cụ thể của phương trình.

Một đặc điểm quan trọng của phương trình bậc 3 là nó luôn có ít nhất một nghiệm thực và có thể có tối đa ba nghiệm thực phân biệt. Điều này được chứng minh thông qua định lý cơ bản của đại số và tính chất liên tục của hàm số bậc 3. Việc xác định số lượng nghiệm thực có thể dựa vào việc phân tích biệt thức của phương trình.

Cách tính delta và ý nghĩa của delta trong phương trình bậc 3

Delta phương trình bậc 3 là một yếu tố quan trọng giúp xác định bản chất và số lượng nghiệm của phương trình. Khi tính toán delta bậc 3, ta có thể dự đoán được số nghiệm thực và nghiệm phức của phương trình.

Việc tính delta của phương trình bậc 3 giúp ta tiết kiệm thời gian giải phương trình, bởi từ giá trị delta có thể biết được số lượng nghiệm mà không cần giải chi tiết. Đây là phương pháp hiệu quả được áp dụng rộng rãi trong toán học và các ứng dụng thực tế.

Công thức tính delta của phương trình bậc 3

Với phương trình bậc 3 có dạng tổng quát ax³ + bx² + cx + d = 0 (a ≠ 0), ta có công thức tính delta như sau:
Delta = 18abcd – 4b³d + b²c² – 4ac³ – 27a²d²

Để áp dụng công thức này một cách chính xác, cần lưu ý các hệ số a, b, c, d phải được xác định đúng từ phương trình đã cho. Trong trường hợp phương trình chưa ở dạng chuẩn, ta cần biến đổi về dạng tổng quát trước khi tính delta phương trình bậc 3.

Mối quan hệ giữa delta và số nghiệm của phương trình

Giá trị của delta quyết định trực tiếp đến số lượng và tính chất của nghiệm phương trình bậc 3. Khi delta > 0, phương trình có 3 nghiệm thực phân biệt. điều kiện phương trình bậc 3 có 3 nghiệm

Khi delta = 0, phương trình có ít nhất một nghiệm thực kép. Trường hợp này có thể xảy ra theo hai cách: hoặc có một nghiệm kép và một nghiệm đơn, hoặc có một nghiệm bậc ba.

Khi delta < 0, phương trình có một nghiệm thực và hai nghiệm phức liên hợp. Điều này có ý nghĩa quan trọng trong các bài toán vật lý và kỹ thuật, nơi nghiệm phức thường mang những ý nghĩa vật lý đặc biệt.

Phương pháp giải và tìm nghiệm của phương trình bậc 3

Để tìm nghiệm của phương trình bậc 3, có hai phương pháp chính được sử dụng phổ biến là công thức Cardan và phương pháp phân tích nhân tử. Mỗi phương pháp đều có những ưu điểm và hạn chế riêng, phù hợp với từng dạng phương trình cụ thể.

Việc lựa chọn phương pháp giải phù hợp sẽ giúp tiết kiệm thời gian và đạt kết quả chính xác. Trong nhiều trường hợp, phương trình bậc 3 có 3 nghiệm và việc tìm ra tất cả các nghiệm đòi hỏi phải áp dụng đúng phương pháp.

Công thức Cardan giải phương trình bậc 3

Công thức phương trình bậc 3 Cardan là phương pháp tổng quát để giải mọi phương trình bậc 3. Phương pháp này do nhà toán học người Ý Gerolamo Cardano phát triển vào thế kỷ 16.

Công thức này đặc biệt hiệu quả khi phương trình ở dạng chuẩn ax³ + bx² + cx + d = 0. Tuy nhiên, việc áp dụng công thức đòi hỏi nhiều bước tính toán phức tạp và dễ sai sót nếu không cẩn thận.

Trong thực tế, công thức Cardan thường được sử dụng khi các phương pháp đơn giản hơn không áp dụng được. Đây là công cụ quan trọng trong lý thuyết đại số và có nhiều ứng dụng trong khoa học kỹ thuật.

Phương pháp nhân tử phân tích tam thức bậc 3

Phân tích tam thức bậc 3 thành nhân tử là phương pháp trực quan và hiệu quả khi có thể đoán được một nghiệm của phương trình. Phương pháp này đặc biệt phù hợp với các bài toán thực tế.

Khi phân tích được thành nhân tử, việc tìm các nghiệm còn lại trở nên đơn giản hơn nhiều so với sử dụng công thức Cardan. Tuy nhiên, khó khăn lớn nhất là phải tìm được nghiệm đầu tiên.

Trong giảng dạy và học tập, phương pháp này thường được ưu tiên sử dụng vì tính trực quan và dễ hiểu của nó. Nhiều bài toán trong chương trình phổ thông được thiết kế để có thể giải bằng phương pháp này.

Cách phân tích tam thức bậc 3 khi biết một nghiệm

Khi đã biết một nghiệm x₁ của phương trình, ta có thể chia đa thức bậc 3 cho (x – x₁) để được thương là một đa thức bậc 2. Phương pháp này giúp đơn giản hóa việc tìm các nghiệm còn lại.

Quá trình phân tích cần được thực hiện cẩn thận và có hệ thống để tránh sai sót. Việc kiểm tra lại kết quả bằng cách thế các nghiệm vào phương trình ban đầu là rất quan trọng.

Trong nhiều trường hợp, nghiệm đầu tiên có thể được tìm thấy bằng cách quan sát hoặc thử các số hợp lý. Điều này đặc biệt đúng với các phương trình có hệ số nguyên và nghiệm hữu tỷ.

Định lý Vi-ét và ứng dụng trong phương trình bậc 3

Định lý Vi-ét là một công cụ quan trọng giúp giải quyết các bài toán liên quan đến viet hàm bậc 3. Định lý này thiết lập mối liên hệ giữa các nghiệm và hệ số của phương trình, từ đó tạo điều kiện thuận lợi cho việc tìm nghiệm.

Khi áp dụng định lý Vi-ét vào phương trình bậc 3, ta có thể xác định được mối quan hệ giữa tổng, tích và tổng các tích từng cặp nghiệm với các hệ số của phương trình. Điều này giúp đơn giản hóa quá trình giải phương trình và kiểm tra kết quả.

Hệ thức Vi-ét cho phương trình bậc 3

Đối với vi-ét bậc 3, khi xét phương trình ax³ + bx² + cx + d = 0 (a ≠ 0) với ba nghiệm x₁, x₂, x₃, ta có các hệ thức cơ bản sau:
x₁ + x₂ + x₃ = -b/a
x₁x₂ + x₂x₃ + x₃x₁ = c/a
x₁x₂x₃ = -d/a

Các hệ thức này có ý nghĩa quan trọng trong việc phân tích tính chất của nghiệm. Khi áp dụng quy tắc xét dấu của hàm bậc 3 có 3 nghiệm, ta có thể xác định được dấu và quan hệ giữa các nghiệm một cách hiệu quả.

Cách áp dụng Vi-ét để tìm nghiệm

Khi giải viet phương trình bậc 3, việc áp dụng Vi-ét thường được thực hiện theo hai bước chính. Đầu tiên, ta đưa phương trình về dạng chuẩn bằng cách chia toàn bộ phương trình cho hệ số của x³.

Tiếp theo, sử dụng các hệ thức Vi-ét để thiết lập hệ phương trình giữa các nghiệm. Phương pháp này đặc biệt hiệu quả khi một trong các nghiệm đã được biết trước hoặc khi có thêm điều kiện bổ sung về mối quan hệ giữa các nghiệm.

Trong nhiều trường hợp, việc kết hợp Vi-ét với các phương pháp khác như phương pháp thế, phương pháp nhóm hạng tử sẽ giúp quá trình giải phương trình trở nên đơn giản và hiệu quả hơn.

Các dạng bài tập thường gặp về phương trình bậc 3

Việc nắm vững các dạng bài tập về phương trình bậc 3 giúp học sinh phát triển tư duy giải tích và kỹ năng giải quyết vấn đề toán học. Các bài tập thường xuất hiện trong chương trình phổ thông và thi đại học đòi hỏi nhiều phương pháp giải khác nhau.

Để giải thành công các bài toán về pt bậc 3, học sinh cần kết hợp kiến thức từ nhiều phần như phương trình bậc nhất hai ẩn là gì và các phương pháp giải tích cơ bản. Việc rèn luyện qua nhiều dạng bài tập sẽ giúp nâng cao khả năng tư duy và kỹ năng tính toán.

Bài tập về tìm nghiệm phương trình bậc 3

Dạng bài tập tìm nghiệm thường yêu cầu học sinh áp dụng các phương pháp như phân tích thừa số, đặt ẩn phụ hoặc công thức Cardano. Việc nhận biết đúng dạng bài tập sẽ giúp chọn được phương pháp giải phù hợp nhất.

Khi giải các bài toán phức tạp hơn như phương trình mặt phẳng đi qua 3 điểm, học sinh cần kết hợp kiến thức về phương trình bậc 3 với hình học không gian. Điều này đòi hỏi khả năng tổng hợp và vận dụng kiến thức linh hoạt.

Một số kỹ thuật quan trọng khi giải bài tập tìm nghiệm bao gồm: kiểm tra tính chất của hệ số, xét dấu của biểu thức delta, và áp dụng các công thức nghiệm đặc biệt. Việc thực hành nhiều sẽ giúp nâng cao độ chính xác và tốc độ giải.

Bài tập về ứng dụng Vi-ét trong phương trình bậc 3

Định lý Vi-ét là công cụ mạnh mẽ giúp thiết lập mối quan hệ giữa các nghiệm và hệ số của phương trình. Các bài tập ứng dụng Vi-ét thường yêu cầu tính tổng, tích hoặc các biểu thức đối xứng của nghiệm.

Khi áp dụng Vi-ét, học sinh cần chú ý đến dạng chuẩn của phương trình và các hệ thức cơ bản. Việc nắm vững các công thức Vi-ét mở rộng sẽ giúp giải nhanh nhiều bài toán phức tạp.

Các bài tập nâng cao thường kết hợp Vi-ét với các phương pháp khác như: quy đổi biểu thức, sử dụng bất đẳng thức, hay chứng minh các mệnh đề về nghiệm. Điều này đòi hỏi sự linh hoạt trong tư duy và khả năng kết hợp nhiều kiến thức.

Phương trình bậc 3 là một trong những kiến thức cơ bản nhưng đầy thú vị trong toán học, giúp học sinh phát triển tư duy và khả năng giải quyết vấn đề. Bài viết đã trình bày rõ ràng về cách tính delta, phương pháp giải và ứng dụng định lý Vi-ét. Kiến thức này không chỉ cung cấp cho bạn công cụ để tìm nghiệm mà còn giúp bạn nâng cao kỹ năng toán học của mình hiệu quả.