Điều kiện để phương trình bậc 3 có 3 nghiệm phân biệt và cách xác định số nghiệm

Điều kiện để phương trình bậc 3 có 3 nghiệm là kiến thức quan trọng trong học toán. Để xác định số nghiệm, bạn cần xem xét đến hệ số và dấu của biệt thức. Bài viết này sẽ cung cấp hướng dẫn chi tiết và công thức cần thiết để ứng dụng vào thực tế.

Điều kiện để phương trình bậc 3 có 3 nghiệm

Để xác định điều kiện để phương trình bậc 3 có 3 nghiệm, trước tiên cần hiểu rằng một phương trình bậc 3 có thể có 1 hoặc 3 nghiệm thực phụ thuộc vào giá trị của biệt thức Δ. Khi Δ < 0, phương trình sẽ có 3 nghiệm thực phân biệt.

Biệt thức Δ của phương trình bậc 3 ax³ + bx² + cx + d = 0 được tính theo công thức: Δ = 18abcd – 4b³d + b²c² – 4ac³ – 27a²d². Để phương trình có 3 nghiệm thực phân biệt, giá trị của biệt thức Δ phải âm và các hệ số a, b, c, d phải thỏa mãn điều kiện tồn tại nghiệm.

Ngoài điều kiện về biệt thức, phương trình bậc 3 còn cần thỏa mãn một số điều kiện bổ sung. Đó là hệ số a ≠ 0 (để đảm bảo là phương trình bậc 3) và các hệ số b, c, d phải là số thực. Khi tất cả các điều kiện này được thỏa mãn, phương trình sẽ có đúng 3 nghiệm thực phân biệt.

Phân tích các dạng nghiệm của phương trình bậc 3 thông qua đồ thị

Phương trình bậc 3 có thể có 1, 2 hoặc 3 nghiệm thực phụ thuộc vào dạng đồ thị của hàm số. Việc phân tích đồ thị giúp xác định được số lượng nghiệm một cách trực quan thông qua các giao điểm với trục hoành.

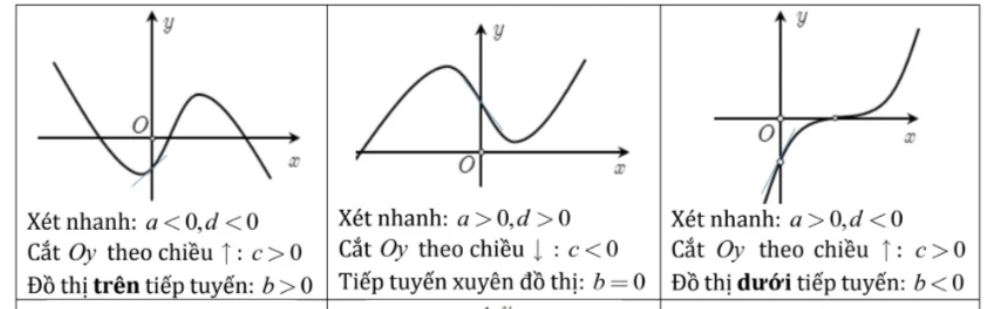
Khi xét về mặt hình học, nghiệm của phương trình bậc 3 chính là hoành độ của các điểm mà đồ thị hàm số cắt trục Ox. Số lượng giao điểm này phụ thuộc vào cách đồ thị uốn cong và vị trí tương đối với trục hoành.

Đồ thị hàm số bậc 3 và mối liên hệ với số nghiệm

Đồ thị của hàm số bậc ba luôn có dạng đường cong liên tục, có một điểm uốn và hai điểm cực trị (nếu có). Khi đồ thị chỉ cắt trục Ox tại một điểm, phương trình có một nghiệm thực duy nhất.

Trong trường hợp đồ thị tiếp xúc với trục Ox tại một điểm và cắt tại điểm còn lại, phương trình sẽ có hai nghiệm, trong đó có một nghiệm kép. xét dấu hàm bậc 3 sẽ giúp xác định chính xác vị trí các điểm này.

Đặc biệt, khi đồ thị cắt trục Ox tại ba điểm khác nhau, phương trình sẽ có ba nghiệm phân biệt. Điều này xảy ra khi đồ thị có hai điểm cực trị nằm ở hai phía của trục Ox.

Điều kiện để có 3 nghiệm phân biệt thông qua đồ thị

Điều kiện để phương trình bậc 3 có 3 nghiệm phân biệt được thể hiện rõ qua hình dạng đồ thị. Điểm cực đại phải nằm phía trên trục Ox và điểm cực tiểu phải nằm phía dưới trục Ox.

Về mặt đại số, điều này tương đương với việc giá trị của hàm số tại điểm cực đại phải dương và giá trị tại điểm cực tiểu phải âm. Khi đó, theo tính liên tục của hàm số, đồ thị buộc phải cắt trục Ox tại ba điểm khác nhau.

Ngoài ra, khoảng cách giữa hai điểm cực trị theo phương ngang càng lớn thì khả năng tồn tại ba nghiệm phân biệt càng cao. Điều này đảm bảo đồ thị có đủ không gian để uốn lượn và tạo ra ba giao điểm với trục hoành.

Điều kiện về hệ số để phương trình bậc 3 có 3 nghiệm thực phân biệt

Để một phương trình bậc 3 có dạng ax³ + bx² + cx + d = 0 (a ≠ 0) có 3 nghiệm thực phân biệt, cần thỏa mãn các điều kiện về hệ số liên quan đến biệt thức Δ và các hệ số a, b, c, d của phương trình.

Các điều kiện về hệ số phương trình được xác định thông qua biệt thức Δ = 18abcd – 4b³d + b²c² – 4ac³ – 27a²d². Khi Δ > 0, phương trình sẽ có 3 nghiệm thực phân biệt. điều kiện để phương trình bậc 3 có 3 nghiệm phân biệt

Phân tích điều kiện về dấu của biệt thức

Biệt thức Δ đóng vai trò quyết định trong việc xác định tính chất nghiệm của phương trình bậc 3. Khi Δ > 0, các nghiệm của phương trình sẽ là 3 số thực phân biệt, không trùng nhau.

Nếu Δ = 0, phương trình sẽ có nghiệm kép hoặc ba nghiệm trùng nhau. Trường hợp này xảy ra khi các hệ số thỏa mãn các điều kiện đặc biệt về mối quan hệ giữa chúng.

Khi Δ < 0, phương trình chỉ có một nghiệm thực duy nhất và hai nghiệm phức liên hợp. Điều này cho thấy tầm quan trọng của việc tính toán và xác định dấu của biệt thức Δ.

Áp dụng định lý Viète cho phương trình bậc 3

Định lý Viète cung cấp các công thức quan trọng liên hệ giữa nghiệm và hệ số của phương trình bậc 3. Với x₁, x₂, x₃ là ba nghiệm của phương trình, các công thức Viète có dạng:
x₁ + x₂ + x₃ = -b/a
x₁x₂ + x₂x₃ + x₃x₁ = c/a
x₁x₂x₃ = -d/a

Khi áp dụng định lý Viète, ta có thể kiểm tra tính hợp lý của nghiệm tìm được và xác minh các điều kiện về điều kiện để phương trình bậc 3 có 3 nghiệm. Đồng thời, định lý cũng giúp ta hiểu rõ hơn về mối quan hệ giữa các nghiệm của phương trình.

Việc kết hợp giữa điều kiện về biệt thức và định lý Viète giúp ta có cái nhìn toàn diện về bản chất của nghiệm phương trình bậc 3, từ đó có thể giải quyết các bài toán liên quan một cách hiệu quả.

Phương pháp xác định số nghiệm của phương trình bậc 3

Để xác định số nghiệm của phương trình bậc 3, ta cần phân tích các yếu tố quyết định như hệ số và đồ thị của hàm số. Phương trình bậc 3 có 3 nghiệm khi nào phụ thuộc vào việc đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

Một yếu tố quan trọng cần xem xét là điều kiện nghiệm thực của phương trình. Khi phương trình có 3 nghiệm phân biệt, các nghiệm này đều phải là số thực và nằm trên trục hoành của đồ thị hàm số bậc 3.

Để giải quyết bài toán tìm m để pt có 3 nghiệm pb, ta cần kết hợp nhiều phương pháp khác nhau như phân tích đồ thị, sử dụng đạo hàm và phương pháp thế.

Sử dụng đạo hàm để xét tính đơn điệu

Đạo hàm là công cụ hiệu quả để xác định tính đơn điệu và các điểm cực trị của hàm số bậc 3. Khi đạo hàm bậc nhất có 2 nghiệm phân biệt, đồ thị hàm số sẽ có 2 điểm cực trị.

Việc phân tích dấu của đạo hàm giúp ta xác định các khoảng đơn điệu tăng, giảm của hàm số. Điều này rất quan trọng vì nó cho biết khả năng cắt trục hoành của đồ thị.

Nếu hai điểm cực trị nằm ở hai phía của trục hoành và hàm số có giá trị dương khi x tiến đến dương vô cùng, phương trình sẽ có đúng 3 nghiệm thực phân biệt.

Phương pháp thế để tìm nghiệm

Sau khi xác định được số nghiệm, ta có thể sử dụng phương pháp thế để tìm các nghiệm cụ thể. Phương pháp này đặc biệt hiệu quả khi ta đã biết một nghiệm của phương trình.

Khi đã tìm được một nghiệm x₁, ta có thể phân tích đa thức thành nhân tử để tìm hai nghiệm còn lại. Quá trình này giúp chuyển bài toán từ giải phương trình bậc 3 thành giải phương trình bậc 2.

Trong một số trường hợp đặc biệt, ta có thể sử dụng các công thức nghiệm tổng quát như công thức Cardano. Tuy nhiên, phương pháp này thường phức tạp và khó áp dụng trong thực tế.

Các trường hợp đặc biệt của phương trình bậc 3

Phương trình bậc 3 có thể có nhiều dạng nghiệm khác nhau tùy thuộc vào các hệ số và điều kiện để pt bậc 3 có 3 nghiệm. Việc phân tích các trường hợp đặc biệt giúp ta hiểu rõ hơn về bản chất và cách giải phương trình. Theo công thức đại số, ta có thể xác định được các dạng nghiệm dựa vào biểu thức delta.

Khi delta > 0, phương trình sẽ có ba nghiệm phân biệt thực. Ngược lại, khi delta < 0, phương trình sẽ có một nghiệm thực và hai nghiệm phức liên hợp. Trường hợp delta = 0 sẽ dẫn đến sự xuất hiện của nghiệm kép.

Phương trình có nghiệm phức

Khi phương trình bậc 3 có nghiệm phức, ta thường gặp một nghiệm thực và hai nghiệm phức liên hợp. Điều này xảy ra khi delta của phương trình nhỏ hơn 0.

Ví dụ với phương trình x³ – 6x + 4 = 0, ta có delta < 0. Phương trình này có một nghiệm thực x₁ = -2 và hai nghiệm phức liên hợp x₂ = 1 + i√3 và x₃ = 1 – i√3.

Việc tìm nghiệm phức đòi hỏi sử dụng các phép tính với số phức và công thức Cardano một cách chính xác.

Phương trình có nghiệm kép

Trường hợp nghiệm kép xuất hiện khi delta = 0, tức là phương trình có hai nghiệm trùng nhau và một nghiệm đơn. Đây là trường hợp đặc biệt thể hiện sự chuyển tiếp giữa trường hợp ba nghiệm thực phân biệt và trường hợp có nghiệm phức.

Một ví dụ điển hình là phương trình x³ – 3x² + 3x – 1 = 0, có nghiệm kép x₁ = x₂ = 1 và nghiệm đơn x₃ = 1. Khi vẽ đồ thị, đường cong sẽ tiếp xúc với trục hoành tại điểm có nghiệm kép.

Nghiệm kép có ý nghĩa quan trọng trong nhiều ứng dụng thực tế, đặc biệt trong các bài toán tối ưu và lý thuyết điều khiển.

Để phương trình bậc 3 có 3 nghiệm, điều kiện cần thiết là phải có 3 nghiệm phân biệt. Việc nắm rõ điều kiện để phương trình bậc 3 có 3 nghiệm không chỉ giúp bạn giải quyết bài toán một cách hiệu quả mà còn là cơ sở kiến thức quan trọng trong môn toán. Hãy tìm hiểu các phương pháp và điều kiện liên quan để áp dụng vào thực tế.