Phương trình hoành độ giao điểm và cách xác định trong hình học phẳng

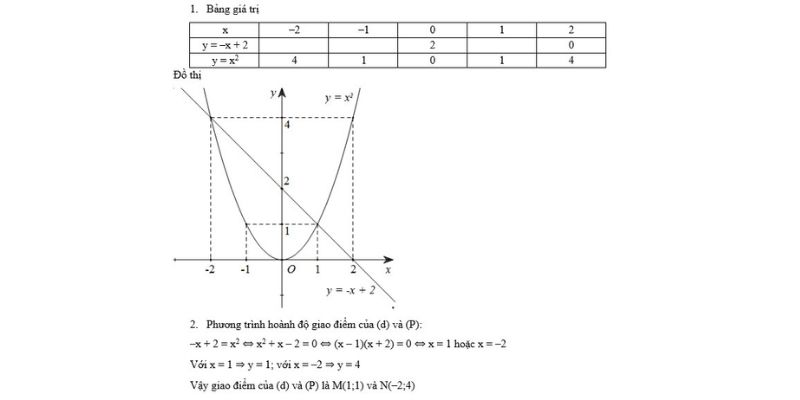
Hoành độ giao điểm là một khái niệm quan trọng trong toán học, đặc biệt trong việc xác định giao điểm của các đường thẳng. Bài viết này sẽ trình bày phương trình hoành độ giao điểm và các phương pháp khác nhau giúp bạn thuần thục trong việc tìm hoành độ. Khám phá ngay để nâng cao kỹ năng toán học của bạn!

Phương trình hoành độ giao điểm và cách xác định trong hệ tọa độ Oxy

Phương trình hoành độ giao điểm là phương trình xác định tọa độ x của điểm mà tại đó hai đường thẳng, đường cong hoặc đồ thị của hai hàm số cắt nhau trong hệ trục tung trục hoành. Để tìm được phương trình này, ta cần giải hệ phương trình của hai đường thẳng hoặc đồ thị đã cho.

Khi hai đồ thị cắt nhau, tọa độ x của điểm giao sẽ là nghiệm của phương trình thu được sau khi giải hệ phương trình. Hoành độ giao điểm là gì? Đó chính là giá trị x tìm được từ phương trình hoành độ, cho biết vị trí chính xác trên trục hoành nơi hai đồ thị gặp nhau.

Để xác định hoành độ giao điểm một cách chính xác, ta thực hiện theo các bước sau: Đầu tiên, lập hệ phương trình từ hai đồ thị. Tiếp theo, biến đổi để thu được phương trình chỉ còn ẩn x. Cuối cùng, giải phương trình để tìm giá trị x – chính là hoành độ của điểm giao cần tìm. Việc xác định hoành độ giao điểm giúp ta biết được vị trí chính xác nơi hai đồ thị gặp nhau trên trục hoành, từ đó có thể tìm được tọa độ đầy đủ của điểm giao.

Các phương pháp tìm hoành độ giao điểm của hai đường thẳng

Phương trình hoành độ giao điểm là gì? Đó chính là phương trình xác định tọa độ x của điểm mà hai đường thẳng cắt nhau. Để tìm được hoành độ giao điểm của hai đường thẳng, có thể áp dụng nhiều phương pháp khác nhau tùy thuộc vào dạng bài toán cụ thể.

Phương pháp giải hệ phương trình tuyến tính

Phương pháp này thường được áp dụng khi hai đường thẳng được cho dưới dạng phương trình tổng quát ax + by + c = 0. Bằng cách giải hệ phương trình của hai đường thẳng, ta sẽ tìm được tọa độ điểm giao.

Khi áp dụng phương pháp này, cần lưu ý rằng nghiệm của hệ phương trình sẽ cho ta cả hoành độ và tung độ của điểm giao. Trong hình học không gian oxyz, phương pháp này còn có thể mở rộng để tìm giao điểm của đường thẳng với mặt phẳng.

Phương pháp thế và phương pháp cộng đại số

Phương pháp thế được sử dụng khi một trong hai đường thẳng có dạng y = ax + b. Ta thay biểu thức của y vào phương trình còn lại để tìm x. Phương pháp này đơn giản và hiệu quả với các phương trình đơn giản.

Phương pháp cộng đại số thường áp dụng khi hai phương trình có hệ số tương đồng. Bằng cách nhân các hệ số thích hợp rồi cộng hoặc trừ hai phương trình, ta có thể loại bỏ một ẩn và tìm được nghiệm dễ dàng.

Phương pháp đồ thị hình học

Phương pháp này sử dụng cách vẽ đồ thị hai đường thẳng trên cùng một hệ trục tọa độ. Tìm hoành độ giao điểm bằng cách xác định tọa độ x của điểm giao cắt trên đồ thị.

Phương pháp đồ thị giúp trực quan hóa bài toán và kiểm chứng kết quả tính toán. Tuy nhiên, độ chính xác phụ thuộc vào kỹ năng vẽ và thước đo được sử dụng. Phương pháp này thường được dùng để ước lượng nghiệm trước khi áp dụng các phương pháp đại số chính xác.

Ứng dụng hoành độ giao điểm trong giải toán hình học phẳng

Phương trình hoành độ giao điểm là công cụ quan trọng giúp xác định vị trí giao nhau của hai đường thẳng trong mặt phẳng tọa độ. Thông qua việc giải phương trình này, ta có thể tìm được tọa độ điểm giao của hai đường thẳng, từ đó phân tích các mối quan hệ hình học.

Khi Học Thế Nào về cách ứng dụng phương trình này, việc xét phương trình hoành độ giao điểm giúp ta giải quyết nhiều bài toán phức tạp về vị trí tương đối và khoảng cách giữa các đối tượng hình học một cách hiệu quả và chính xác.

Xác định vị trí tương đối của hai đường thẳng

Để xác định vị trí tương đối của hai đường thẳng, ta cần phân tích nghiệm của phương trình hoành độ giao điểm. Nếu phương trình có một nghiệm duy nhất, hai đường thẳng cắt nhau tại một điểm. Trường hợp phương trình vô nghiệm chứng tỏ hai đường thẳng song song.

Khi phương trình có vô số nghiệm, điều này cho thấy hai đường thẳng trùng nhau hoàn toàn. Việc phân tích các trường hợp này giúp ta có cái nhìn tổng quát về mối quan hệ hình học giữa các đường thẳng trong mặt phẳng tọa độ.

Tính khoảng cách và góc giữa hai đường thẳng

Sau khi xác định được vị trí tương đối, ta có thể tính toán khoảng cách giữa hai đường thẳng thông qua công thức tổng quát. Đối với hai đường thẳng cắt nhau, góc giữa chúng được xác định bằng công thức lượng giác dựa trên vector pháp tuyến.

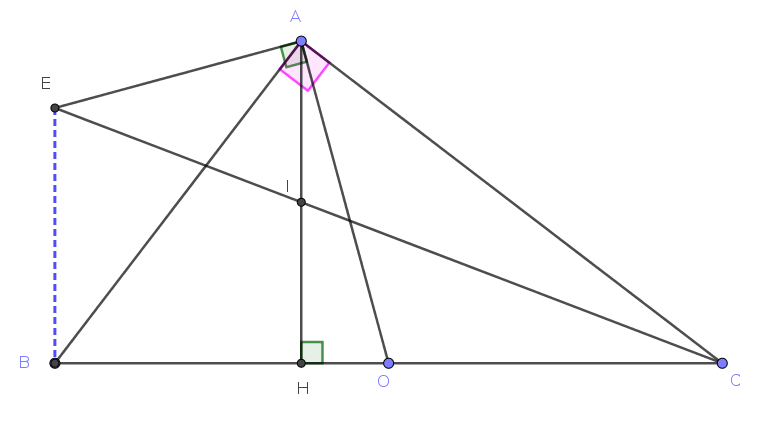
Việc tính toán các đại lượng này có ý nghĩa quan trọng trong nhiều ứng dụng thực tế như thiết kế công trình, quy hoạch đô thị hay các bài toán về chuyển động. Kết quả tính toán chính xác sẽ giúp đưa ra các quyết định phù hợp trong quá trình thiết kế và thi công.

Mối liên hệ giữa hoành độ giao điểm và đồ thị hàm số

Mối liên hệ giữa hoành độ giao điểm và đồ thị hàm số thể hiện qua việc xác định các điểm mà đồ thị cắt trục hoành. Khi một đường thẳng hoặc đường cong cắt trục Ox tại một điểm, hoành độ của điểm đó chính là nghiệm của phương trình f(x) = 0.

Để xác định chính xác các điểm giao, ta cần xét kí hiệu giao giữa đồ thị hàm số và trục hoành. Tọa độ giao điểm có dạng (a,0) trong đó a là nghiệm của phương trình f(x) = 0.

Việc nắm vững mối liên hệ này giúp giải quyết nhiều bài toán về phương trình, đặc biệt là các phương trình phức tạp khó giải bằng phương pháp đại số thông thường.

Xác định giao điểm của đồ thị hàm số với trục hoành

Để xác định giao điểm của đồ thị hàm số với trục hoành, ta cần thực hiện hai bước cơ bản. Đầu tiên, lập phương trình f(x) = 0 vì tại giao điểm với trục Ox, tung độ y luôn bằng 0.

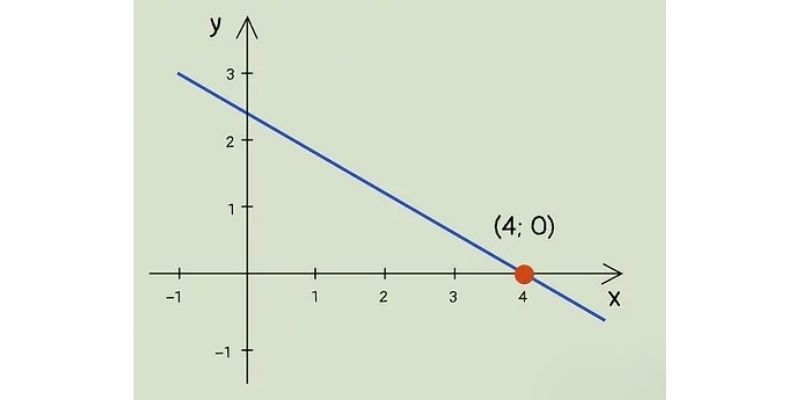
Sau khi giải phương trình f(x) = 0, ta thu được các giá trị x. Mỗi giá trị x tìm được sẽ cho ta một hoành độ của giao điểm. Tọa độ giao điểm hoàn chỉnh sẽ có dạng (x,0).

Ví dụ với hàm số y = x² – 4, phương trình x² – 4 = 0 cho ta x = ±2. Do đó đồ thị hàm số cắt trục Ox tại hai điểm có tọa độ (-2,0) và (2,0).

Tìm nghiệm của phương trình bằng hoành độ giao điểm

Phương pháp tìm nghiệm thông qua hoành độ giao điểm đặc biệt hữu ích khi giải các phương trình phức tạp. Bằng cách vẽ đồ thị và xác định các điểm cắt trục hoành, ta có thể tìm được nghiệm gần đúng của phương trình.

Phương pháp này còn giúp kiểm chứng kết quả tính toán đại số. Nếu nghiệm tìm được bằng cách giải phương trình trùng với hoành độ giao điểm, ta có thể khẳng định kết quả là chính xác.

Trong thực tế, nhiều phần mềm toán học như GeoGebra, Desmos thường sử dụng phương pháp đồ thị để giúp người dùng hình dung và xác định nghiệm của phương trình một cách trực quan.

Bài tập và phương pháp giải về hoành độ giao điểm

Việc tìm hoành độ giao điểm của hai đường thẳng là một kỹ năng quan trọng trong hình học phẳng. Tìm giao điểm hai đường thẳng không chỉ giúp xác định vị trí cắt nhau mà còn là nền tảng để giải quyết nhiều bài toán phức tạp hơn.

Khi giải các bài toán về phương trình đường thẳng, việc xác định hoành độ giao điểm thường đòi hỏi phải giải hệ phương trình. Tương tự như biến cố xung khắc trong xác suất thống kê, hai đường thẳng song song sẽ không có giao điểm.

Để giải quyết các bài toán về pt hoành độ giao điểm, cần nắm vững phương pháp giải hệ phương trình và các tính chất hình học cơ bản. Việc áp dụng đúng công thức và kiểm tra kỹ kết quả sẽ giúp tránh các sai sót không đáng có.

Bài tập cơ bản về tìm hoành độ giao điểm

Các bài tập cơ bản thường yêu cầu tìm hoành độ giao điểm của hai đường thẳng khi biết phương trình của chúng. Phương pháp giải thường bao gồm việc giải hệ phương trình và xác định tọa độ điểm giao cắt.

Một số bài tập đòi hỏi phải biến đổi phương trình về dạng chuẩn trước khi giải. Điều này giúp phát triển kỹ năng biến đổi đại số và tư duy logic trong quá trình giải toán.

Việc kiểm tra lại kết quả bằng cách thế các giá trị tìm được vào phương trình ban đầu là bước quan trọng để đảm bảo độ chính xác của lời giải.

Bài tập nâng cao và ứng dụng thực tế

Các bài tập nâng cao thường kết hợp với các yếu tố hình học khác như đường tròn, parabol hoặc các đường cong bậc cao. Những bài toán này đòi hỏi sự linh hoạt trong việc áp dụng kiến thức và kỹ năng phân tích sâu sắc.

Trong thực tế, việc tìm hoành độ giao điểm được ứng dụng rộng rãi trong nhiều lĩnh vực. Ví dụ, các kỹ sư xây dựng sử dụng kiến thức này để tính toán điểm giao nhau của các kết cấu, hoặc các nhà thiết kế đồ họa áp dụng để xác định vị trí cắt nhau của các đường nét trong thiết kế.

Khả năng giải quyết các bài toán phức tạp về hoành độ giao điểm còn giúp phát triển tư duy không gian và kỹ năng giải quyết vấn đề, những yếu tố quan trọng trong nhiều ngành nghề hiện đại.

Hoành độ giao điểm là khái niệm quan trọng trong toán học, giúp xác định vị trí giao nhau của các đường thẳng. Việc nắm rõ các phương pháp tìm hoành độ giao điểm sẽ hỗ trợ học sinh trong việc giải quyết nhiều bài toán hình học và ứng dụng thực tế. Qua bài viết, bạn không chỉ hiểu sâu sắc về phương trình hoành độ giao điểm mà còn biết cách áp dụng nó một cách hiệu quả trong các bài tập khó khăn hơn.