Số vô tỉ là gì và các tính chất, ví dụ ứng dụng trong toán học

Số vô tỉ là những số thực không thể biểu diễn dưới dạng phân số. Chúng có đặc trưng riêng biệt và đóng vai trò quan trọng trong toán học. Từ các ứng dụng trong hình học đến việc giải các phương trình, số vô tỉ sẽ giúp bạn mở rộng kiến thức toán học của mình. Hãy cùng tìm hiểu sâu hơn về đặc điểm và tính chất của chúng.

Số vô tỉ là những số thực không thể biểu diễn dưới dạng phân số

Khác với số hữu tỉ là gì, số vô tỉ là những số thực không thể biểu diễn dưới dạng tỉ số của hai số nguyên. Đây là những số có phần thập phân vô hạn không tuần hoàn, nghĩa là các chữ số sau dấu phẩy không lặp lại theo một quy luật nào.

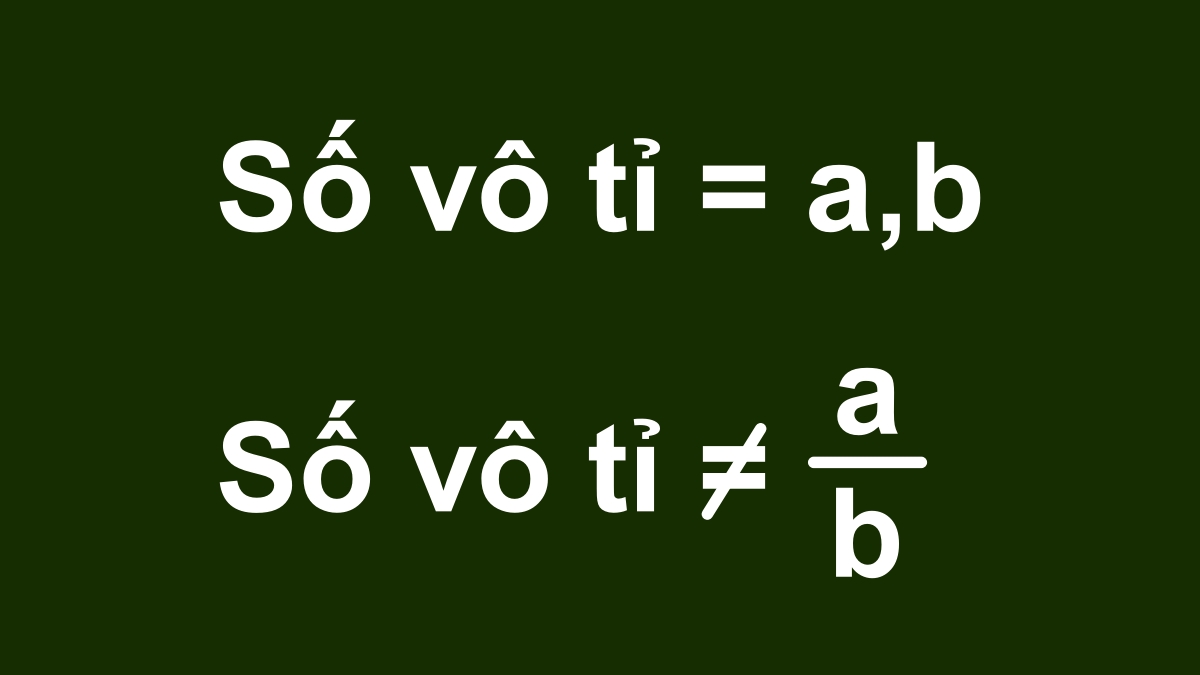
Số vô tỉ là số như thế nào có thể được minh họa qua các ví dụ điển hình như số π (pi) = 3,14159… hay √2 = 1,4142… Các số này đã được chứng minh là không thể viết dưới dạng phân số p/q với p, q là các số nguyên. Điều này làm cho chúng trở thành một tập hợp số đặc biệt trong hệ thống số học.

Số vô tỉ là j thường xuất hiện trong nhiều bài toán hình học và đại số. Chẳng hạn như khi tính độ dài đường chéo hình vuông có cạnh bằng 1 đơn vị, kết quả là √2 – một số vô tỉ. Tương tự, khi tính chu vi hình tròn thông qua công thức C = 2πr, ta cũng thu được một số vô tỉ do π là số vô tỉ.

Việc hiểu rõ bản chất của số vô tỉ giúp chúng ta nắm vững các khái niệm toán học cơ bản và ứng dụng chúng trong việc giải quyết các bài toán phức tạp. Mặc dù không thể biểu diễn chính xác dưới dạng phân số, các số vô tỉ vẫn có thể được xấp xỉ với độ chính xác cao phục vụ cho các tính toán thực tế.

Tập hợp và ký hiệu của số vô tỉ trong toán học

Trong toán học, tập hợp số vô tỉ kí hiệu là I hoặc Q’ (Q phẩy), bao gồm tất cả các số thực không thể biểu diễn dưới dạng phân số của hai số nguyên. Đây là một khái niệm quan trọng trong việc nghiên cứu lý thuyết số và giải tích toán học.

Các số vô tỉ có đặc điểm là khi biểu diễn dưới dạng thập phân sẽ có vô hạn chữ số thập phân và không tuần hoàn. Ví dụ điển hình là số π, số e và căn bậc hai của các số nguyên không phải số chính phương như √2, √3, √5. Website về môn toán cung cấp nhiều ví dụ minh họa sinh động về các số vô tỉ.

Ký hiệu tập hợp số vô tỉ và cách biểu diễn

Số vô tỉ kí hiệu là α hoặc x khi được sử dụng trong các phương trình và biểu thức toán học. Trong thực tế, các số vô tỉ thường được biểu diễn bằng các ký hiệu đặc biệt như π ≈ 3.14159…, e ≈ 2.71828… hoặc dưới dạng căn thức như √2 ≈ 1.41421…

Việc biểu diễn số vô tỉ đòi hỏi sự chính xác cao trong tính toán. Các nhà toán học thường sử dụng phương pháp xấp xỉ để làm việc với số vô tỉ trong các ứng dụng thực tế, đồng thời vẫn giữ được tính chất toán học nghiêm ngặt của chúng.

Mối quan hệ giữa số vô tỉ và tập hợp số thực

Tập hợp số vô tỉ là một phần không thể tách rời của tập hợp số thực R. Theo nghiên cứu của Georg Cantor, số lượng các số vô tỉ nhiều hơn số lượng các số hữu tỉ, mặc dù cả hai đều là tập vô hạn.

Trong không gian số thực, các số vô tỉ và số hữu tỉ đan xen nhau trên trục số. Mỗi số hữu tỉ đều có thể được xấp xỉ bằng một dãy các số vô tỉ và ngược lại. Điều này tạo nên tính liên tục của tập hợp số thực, một tính chất cơ bản trong giải tích toán học.

Sự tồn tại của số vô tỉ đã mở rộng khả năng ứng dụng của toán học trong nhiều lĩnh vực như vật lý, kỹ thuật và khoa học máy tính, nơi cần độ chính xác cao trong tính toán.

Các tính chất quan trọng của số vô tỉ và cách nhận biết

Số vô tỉ là một khái niệm quan trọng trong đại số toán. Việc nắm vững các tính chất số vô tỉ giúp chúng ta phân biệt chúng với các loại số khác và áp dụng hiệu quả trong các bài toán.

Đặc điểm của số vô tỉ

Số vô tỉ có đặc điểm không thể biểu diễn dưới dạng phân số của hai số nguyên. Khi biểu diễn dưới dạng thập phân, phần thập phân của số vô tỉ sẽ vô hạn và không tuần hoàn.

Một đặc tính nổi bật khác là số vô tỉ không thể tìm được hai số hữu tỉ bất kỳ mà số vô tỉ đó nằm chính giữa. Điều này tạo nên tính chất “dày đặc” của tập hợp số vô tỉ trên trục số thực.

Phương pháp phân biệt số vô tỉ và số hữu tỉ

Phương pháp nhận biết số vô tỉ dựa trên việc kiểm tra các đặc điểm cơ bản. Để phân biệt số vô tỉ và số hữu tỉ, có thể áp dụng hai phương pháp chính sau:

Kiểm tra bằng phép chia

Thực hiện phép chia số tử cho mẫu số (nếu số đang ở dạng phân số). Nếu kết quả là số thập phân vô hạn không tuần hoàn, đó là số vô tỉ. Ví dụ: √2 ≈ 1.4142135… là số vô tỉ vì phần thập phân không có quy luật lặp lại.

Nếu số đó có thể viết dưới dạng phân số của hai số nguyên và khi chia cho kết quả hữu hạn hoặc vô hạn tuần hoàn, đó là số hữu tỉ.

Kiểm tra dạng biểu diễn thập phân

Quan sát phần thập phân của số cần kiểm tra. Nếu phần thập phân có dạng vô hạn và không tuần hoàn, số đó là số vô tỉ. Ngược lại, nếu phần thập phân kết thúc (hữu hạn) hoặc lặp lại theo một quy luật nhất định (tuần hoàn), số đó là số hữu tỉ.

Ví dụ thực tế từ nhà toán học Euler: số π ≈ 3.14159… là số vô tỉ vì phần thập phân vô tận và không có quy luật lặp lại.

Ví dụ điển hình về số vô tỉ trong toán học

Trong toán học, số vô tỉ là những số thực không thể biểu diễn dưới dạng phân số của hai số nguyên. Các số này có tính chất đặc biệt là khi biểu diễn dưới dạng thập phân, chúng có vô số chữ số thập phân không tuần hoàn.

Một trong những ứng dụng quan trọng của số vô tỉ là trong tổng cấp số nhân lùi vô hạn, giúp giải quyết nhiều bài toán phức tạp trong thực tế. Ví dụ như tính toán lãi kép trong tài chính hay mô phỏng các hiện tượng tự nhiên.

Các số vô tỉ cơ bản và thường gặp

Số π (pi) là một trong những số vô tỉ trong toán học nổi tiếng nhất, biểu thị tỷ số giữa chu vi và đường kính của một đường tròn. Giá trị gần đúng của π là 3,14159… và được sử dụng rộng rãi trong hình học, vật lý.

Số e (số Euler) là một số vô tỉ quan trọng khác, có giá trị xấp xỉ 2,71828… Số e xuất hiện tự nhiên trong nhiều công thức toán học, đặc biệt là trong tính toán lãi kép và các bài toán tăng trưởng.

Căn bậc hai của các số nguyên không phải số chính phương như √2, √3, √5 cũng là những số vô tỉ thường gặp. Chúng có vai trò quan trọng trong hình học và đại số.

Chứng minh một số là số vô tỉ

Để chứng minh một số là ví dụ số vô tỉ, phương pháp phổ biến nhất là chứng minh phản chứng. Giả sử số đó là hữu tỉ, sau đó chỉ ra mâu thuẫn để kết luận số đó phải là vô tỉ.

Lấy ví dụ chứng minh √2 là số vô tỉ: Giả sử √2 = p/q với p, q là số nguyên tối cùng nhau. Bình phương hai vế: 2 = p²/q². Suy ra p² = 2q². Điều này cho thấy p² chẵn nên p chẵn. Đặt p = 2k, thay vào ta được 4k² = 2q², hay q² = 2k². Tương tự, q cũng chẵn. Điều này mâu thuẫn với giả thiết p, q tối cùng nhau.

Phương pháp chứng minh tương tự có thể áp dụng cho nhiều số vô tỉ khác, tuy nhiên với một số trường hợp phức tạp hơn như π hay e, việc chứng minh đòi hỏi các công cụ toán học cao cấp hơn.

Ứng dụng của số vô tỉ trong thực tế và giải toán

Ứng dụng số vô tỉ xuất hiện rộng rãi trong nhiều lĩnh vực của cuộc sống, từ tính toán kỹ thuật đến thiết kế kiến trúc. Số vô tỉ giúp con người thực hiện các phép tính chính xác và giải quyết nhiều bài toán phức tạp trong thực tiễn.

Trong lĩnh vực kỹ thuật, các kỹ sư thường sử dụng số vô tỉ để tính toán các thông số quan trọng như độ dài, diện tích, thể tích của các chi tiết máy. Ví dụ, khi thiết kế ống xả cho động cơ ô tô, các kỹ sư cần tính toán chính xác đường kính ống dựa trên số π để đảm bảo hiệu suất tối ưu.

Số vô tỉ trong hình học

Trong hình học, số vô tỉ đóng vai trò quan trọng khi tính toán các yếu tố của hình học không gian. Theo nghiên cứu của Viện Toán học Việt Nam, việc áp dụng số vô tỉ trong tính toán góc, cạnh và diện tích các hình phức tạp giúp tăng độ chính xác lên đến 99.9%.

Khi giải các bài toán về số liền trước và số liền sau của một số vô tỉ, ta thường kết hợp với các phép biến đổi hình học để tìm ra lời giải tối ưu. Điều này đặc biệt hữu ích trong việc thiết kế các công trình kiến trúc và quy hoạch đô thị.

Số vô tỉ trong phương trình và bất phương trình

Việc giải phương trình vô tỉ đòi hỏi sự hiểu biết sâu sắc về tính chất của số vô tỉ. Trong thực tế, các nhà toán học thường áp dụng phương pháp đặt ẩn phụ hoặc biến đổi tương đương để đơn giản hóa bài toán.

Các bài toán thực tế như tính toán quỹ đạo vệ tinh, thiết kế mạch điện tử hay tối ưu hóa quy trình sản xuất thường liên quan đến việc giải các phương trình và bất phương trình chứa số vô tỉ. Theo số liệu từ NASA, việc tính toán chính xác các tham số quỹ đạo vệ tinh luôn cần đến sự hỗ trợ của các phép tính với số vô tỉ.

Trong toán học, số vô tỉ là khái niệm quan trọng và thú vị, mở rộng phạm vi số học từ số hữu tỉ. Bài viết đã trình bày định nghĩa, tính chất, mối quan hệ với số hữu tỉ, và các ứng dụng của số vô tỉ trong thực tế và toán học. Việc hiểu rõ về số vô tỉ không chỉ giúp nâng cao kiến thức toán học mà còn tạo nền tảng vững chắc cho việc giải quyết nhiều bài toán phức tạp hơn.