Khám phá thế giới hình học không gian cùng thể tích hình lập phương là một kỹ năng khá quan trọng mà bạn cần phải hiểu và biết đến. Qua bài viết này bạn sẽ hiểu vì sao thể tích khối lập phương mang lại lợi ích trong thực tiễn và nhiều lĩnh vực khác nhau.
Thể tích hình lập phương là gì?
Hình lập phương là khối hình đặc biệt với 3 chiều, 6 mặt vuông góc với nhau, tạo thành 12 cạnh với các mặt đều là hình vuông có số đo bằng nhau và 8 đỉnh. Thể tích khối lập phương là số đo cho không gian chứa ở bên trong hình ấy.
Khối lập phương sở hữu các tính chất dễ nhìn thấy bằng mắt thường. Cụ thể:
- Tổng cộng 6 mặt phẳng bằng nhau.
- Có 12 cạnh đều.
- Đường chéo các mặt đều như nhau.
- Tất cả các khối hình lập phương bằng nhau.
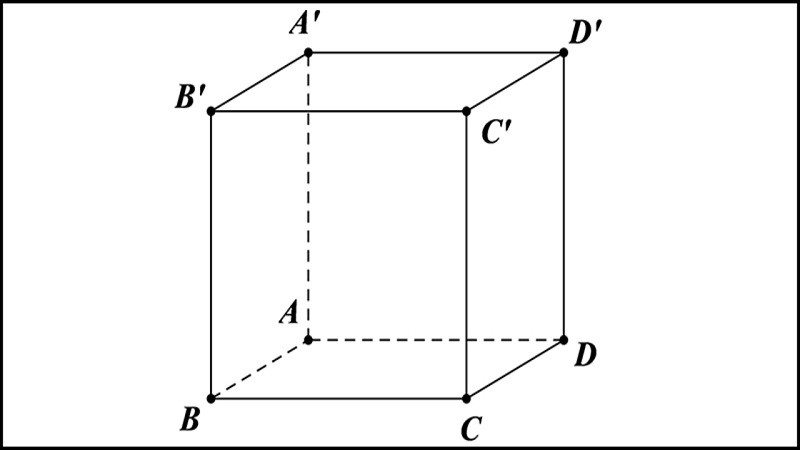
Công thức tính thể tích hình lập phương và các ví dụ
Mặc dù cách tính thể tích khá đơn giản nhưng vẫn còn rất nhiều bạn nhầm lẫn, thậm chí là ghi sai công thức. Điều này gây ra nhiều bất lợi từ học tập đến áp dụng công thức vào đời sống hằng ngày.
Tính thể tích hình lập phương
Để tính thể tích với công thức vô cùng dễ nhớ, bạn chỉ cần biết độ dài của 1 cạnh. Sau đó ta lấy số đo ba cạnh nhân lại với nhau. Hay nói cách khác thể tích hình lập phương bằng tích của độ dài ba cạnh.
Công thức bằng lời như sau:
V = cạnh x cạnh x cạnh
Hay viết dưới dạng toán học:
$$V=a*a*a=a^3$$
Trong đó:
- V: thể tích hình lập phương có đơn vị là cm3, m3,…
- a: độ dài xác định của 1 cạnh trong khối lập phương.
Ví dụ, 1 hình lập phương có độ dài cạnh là 5 cm. Vậy thể tích được tính như sau:
$$V=a\times a\times a=5\times5\times5=125(cm3)$$
Đối với hình lập phương có cạnh a, bạn cần chú ý đặc biệt với những nội dung sau đây để nhanh chóng tìm ra được độ dài của cạnh khi chưa có bất kỳ dữ kiện nào:
- Độ dài đường chéo của khối lập phương có công thức:
$$d=a^3$$
- Độ dài đường chéo ở từng mặt của hình lập phương là:
$$a^2$$
$$Stp=6\times a^2$$
- Diện tích xung quanh của hình lập phương:
$$Sxq=a\times a\times4$$
Một số ví dụ minh họa về cách tính thể tích khối lập phương
Dưới đây chúng tôi sẽ đưa ra 1 vài bài tập cơ bản giúp bạn luyện tập sau khi đã được cung cấp toàn bộ công thức bên trên. Đồng thời, kèm thời lời giải chi tiết để bạn tiện theo dõi từng bước và tự bản thân thực hành thành công.
Bài tập: Tính thể tích của 1 khối lập phương khi biết độ dài 1 cạnh là 4 cm. Nhìn vào đề bài, hãy áp dụng ngay công thức tính ở trên:
$$V=a\times a\times a=4\times4\times4=64(cm3)$$ hoặc $$V=a^3=4^3=64(cm3)$$.
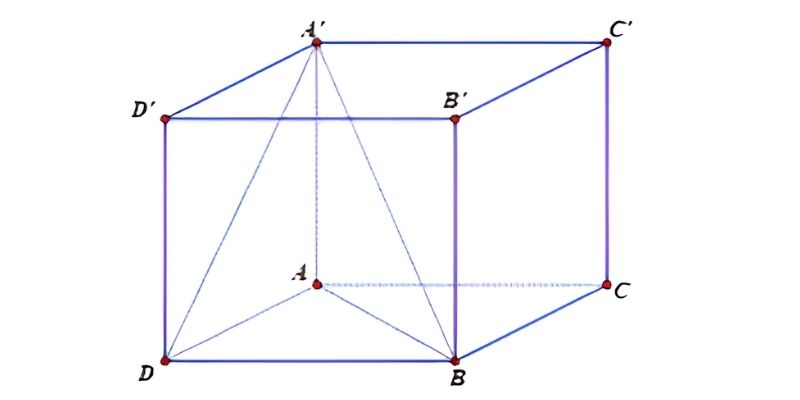Ứng dụng công thức thể tích khối lập phương trong thực tế
Không thể phủ nhận rằng công thức tính thể tích của khối lập phương mang lại nhiều lợi ích đầy thú vị trong cuộc sống. Cụ thể như sau:
- Xây dựng và các công trình kiến trúc: Khi chuẩn bị thiết kế nhà ở, văn phòng, trường học, bệnh viện,… việc biết tính thể tích hình lập phương cực kỳ quan trọng. Kỹ sư sẽ xác định được kích thước, diện tích, vật liệu cần cung ứng vào các công trình đó.
- Tạo sản phẩm: Nhiều sản phẩm công nghiệp như thùng chứa, hộp đựng, bao bì cần áp dụng công thức trên để tính chính xác sản phẩm. Có như vậy mới đáp ứng đủ điều kiện nhu cầu sử dụng và vận chuyển.
- Tính toán thể tích vật chất: Một vài lĩnh vực như: vật lý, kỹ thuật, hóa học cần xác định đúng thể tích của các chất lỏng, rắn đặc biệt quan trọng.
- Toán học & giáo dục: Với một hình lập phương biết trước thể tích, bạn có thể áp dụng công thức và tính toán được độ dài cạnh, từ đó biết được diện tích và chu vi của hình lập phương.
- Lưu trữ và vận chuyển: Trong các hoạt động di chuyển hàng hóa, việc bạn biết cách tính toán thể tích khối lập phương ở các thùng, kiện hàng để tối ưu hóa không gian vận hành sản phẩm.
Kết luận
Trên đây chúng tôi đã đưa ra toàn bộ thông tin đầy đủ về các công thức tính thể tích hình lập phương cùng các bài tập kèm đáp án chi tiết có thể tự học. Bên cạnh đó, bạn cũng biết được tầm quan trọng vốn có của công thức này khi đưa vào sử dụng trong đời sống thực.
