Bất đẳng thức bunhiacopxki và ứng dụng trong toán học cơ bản

Bất đẳng thức Bunhiacopxki là một trong những nội dung quan trọng trong toán học, giúp học sinh nắm vững các ứng dụng và định lý cơ bản. Bài viết sẽ hướng dẫn cụ thể cách chứng minh và áp dụng bất đẳng thức này cho 2 số, mở rộng cho 3 số và nhiều số khác. Thông qua bài giảng này, bạn sẽ khám phá những mẹo hữu ích trong việc giải bài tập và hiểu sâu về các biến thể của bất đẳng thức Bunhiacopxki.

Bất đẳng thức Bunhiacopxki và các ứng dụng cơ bản trong toán học

Bất đẳng thức Bunhiacopxki là một công cụ toán học quan trọng được phát biểu bởi nhà toán học người Nga Viktor Yakovlevich Bunyakovsky vào năm 1859. Bất đẳng thức này cho thấy mối liên hệ giữa tích phân của tích hai hàm số và tích của tích phân từng hàm số riêng biệt.

Trong lĩnh vực giải tích toán học, bđt bunhiacopxki và ứng dụng của nó đóng vai trò then chốt trong việc chứng minh nhiều định lý và giải quyết các bài toán phức tạp. Bất đẳng thức này thường được áp dụng trong không gian Hilbert và các lĩnh vực toán học hiện đại khác như lý thuyết xác suất, thống kê toán học.

Một trong những ứng dụng quan trọng của bất đẳng thức Bunhiacopxki là trong việc ước lượng và đánh giá các đại lượng trong lý thuyết xác suất. Chẳng hạn, khi tính toán phương sai của một biến ngẫu nhiên, bất đẳng thức này giúp thiết lập mối quan hệ giữa kỳ vọng của tích hai biến ngẫu nhiên và tích kỳ vọng của từng biến.

Ngoài ra, bất đẳng thức này còn được ứng dụng rộng rãi trong lý thuyết tối ưu, lý thuyết điều khiển và các bài toán biên. Các nhà nghiên cứu tại Đại học Stanford đã sử dụng bất đẳng thức Bunhiacopxki để phát triển các thuật toán tối ưu trong học máy và trí tuệ nhân tạo, đặc biệt trong việc huấn luyện các mô hình học sâu.

Cách chứng minh và áp dụng bất đẳng thức Bunhiacopxki cho 2 số thực

Bất đẳng thức Bunhiacopxki cho 2 số là một công cụ toán học quan trọng giúp chứng minh nhiều bài toán phức tạp. Bất đẳng thức này có mối liên hệ chặt chẽ với bất đẳng thức cauchy schwarz và thường được sử dụng song song trong các bài toán.

Để áp dụng hiệu quả bất đẳng thức này, cần nắm vững cách chứng minh và các dạng biến thể khác nhau. Việc hiểu rõ bản chất của bất đẳng thức sẽ giúp giải quyết nhiều bài toán về giá trị lớn nhất, nhỏ nhất một cách nhanh chóng và chính xác.

Phát biểu và chứng minh bất đẳng thức Bunhiacopxki cho 2 số

Với mọi số thực dương a và b, ta luôn có: (a + b)² ≥ 4ab. Dấu “=” xảy ra khi và chỉ khi a = b.

Chứng minh bất đẳng thức này có thể thực hiện qua hai cách chính:

Cách 1: Biến đổi vế trái thành (a + b)² – 4ab = (a – b)² ≥ 0. Điều này luôn đúng với mọi số thực a, b và dấu “=” xảy ra khi và chỉ khi a = b.

Cách 2: Áp dụng phương pháp chứng minh bằng cách khai triển: (a + b)² = a² + 2ab + b² ≥ 4ab. Suy ra a² – 2ab + b² ≥ 0, tương đương (a – b)² ≥ 0.

Các dạng bài tập điển hình về bất đẳng thức Bunhiacopxki 2 số

Dạng 1: Chứng minh bất đẳng thức trực tiếp bằng cách áp dụng công thức gốc. Ví dụ: Chứng minh (x + 1/x)² ≥ 4 với mọi x > 0.

Dạng 2: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức. Trong trường hợp này, ta thường đặt ẩn phụ để đưa về dạng chuẩn của bất đẳng thức.

Dạng 3: Kết hợp với các bất đẳng thức khác như Cauchy để giải quyết các bài toán phức tạp hơn. Ví dụ: Chứng minh (a + b)²/(4ab) ≥ 1 với mọi a, b > 0.

Việc nắm vững các dạng bài tập này sẽ giúp người học phát triển kỹ năng giải toán và tư duy logic tốt hơn.

Mở rộng bất đẳng thức Bunhiacopxki cho 3 số và nhiều số

Bất đẳng thức Bunhiacopxki có thể được mở rộng cho trường hợp 3 số và nhiều số, giúp giải quyết các bài toán phức tạp hơn trong đại số. Đây là một công cụ quan trọng trong việc chứng minh các bất đẳng thức và có mối liên hệ chặt chẽ với bất đẳng thức am-gm.

Việc mở rộng bất đẳng thức Bunhiacopxki cho 3 số giúp ta có thêm nhiều phương pháp giải quyết các bài toán về bất đẳng thức. Đặc biệt, khi kết hợp với các bất đẳng thức cơ bản khác, nó trở thành công cụ mạnh mẽ trong việc chứng minh các mệnh đề toán học phức tạp.

Phát biểu và chứng minh bất đẳng thức Bunhiacopxki cho 3 số

Với ba số thực dương a, b, c, ta có bất đẳng thức:
(a² + b²)(b² + c²)(c² + a²) ≥ 4abc(ab + bc + ca)

Để chứng minh bất đẳng thức này, ta có thể sử dụng phương pháp biến đổi đại số kết hợp với bất đẳng thức Cauchy. Đầu tiên, ta đặt x = a/b, y = b/c, z = c/a.

Khi đó, xyz = 1 và bất đẳng thức trên tương đương với:
(1 + x²)(1 + y²)(1 + z²) ≥ 4(x + y + z)

Các ví dụ minh họa và bài tập áp dụng

Một ví dụ điển hình về ứng dụng của bunhiacopxki 3 số là bài toán tìm giá trị nhỏ nhất của biểu thức (a² + b²)(b² + c²)(c² + a²) với điều kiện abc = 1.

Bài toán này có thể được giải quyết bằng cách áp dụng trực tiếp bất đẳng thức đã chứng minh. Khi abc = 1, ta có ab + bc + ca ≥ 3 (theo bất đẳng thức AM-GM).

Một ứng dụng khác là trong việc chứng minh các bất đẳng thức liên quan đến tổng và tích của các số dương. Ví dụ, khi giải bài toán tìm giá trị lớn nhất của tích (a² + b²)(b² + c²)(c² + a²) với điều kiện a + b + c = const.

Ứng dụng bất đẳng thức Bunhiacopxki trong chương trình toán lớp 9

Bất đẳng thức bunhiacopxki lớp 9 là một công cụ toán học quan trọng giúp giải quyết nhiều bài toán về so sánh đại lượng. Bất đẳng thức này thường được áp dụng khi cần chứng minh tổng bình phương các số lớn hơn hoặc bằng bình phương của tổng các số chia cho số lượng phần tử.

Việc nắm vững bất đẳng thức này giúp học sinh giải được nhiều dạng toán phức tạp, đặc biệt trong các bài toán về giá trị lớn nhất, nhỏ nhất. Ngoài ra, nó còn có mối liên hệ chặt chẽ với bất đẳng thức cosi trong việc chứng minh các bất đẳng thức phức tạp hơn.

Các dạng bài tập thường gặp

Dạng 1: Chứng minh bất đẳng thức trực tiếp bằng cách áp dụng công thức Bunhiacopxki. Đây là dạng cơ bản nhất giúp học sinh làm quen với cách sử dụng bất đẳng thức.

Dạng 2: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức. Trong dạng này, học sinh cần kết hợp Bunhiacopxki với các phương pháp biến đổi đại số để đưa về dạng quen thuộc.

Dạng 3: Chứng minh bất đẳng thức có chứa tham số. Đây là dạng nâng cao, đòi hỏi kỹ năng phân tích và xét các trường hợp của tham số.

Phương pháp giải và một số mẹo hay

Bước đầu tiên khi giải các bài toán về bất đẳng thức Bunhiacopxki là nhận diện được dạng bài. Cần xác định rõ các đại lượng cần so sánh và mối quan hệ giữa chúng.

Một mẹo hữu ích là luôn cố gắng đưa biểu thức về dạng tổng bình phương các số trừ đi bình phương của trung bình cộng. Điều này giúp áp dụng bất đẳng thức một cách trực tiếp và hiệu quả.

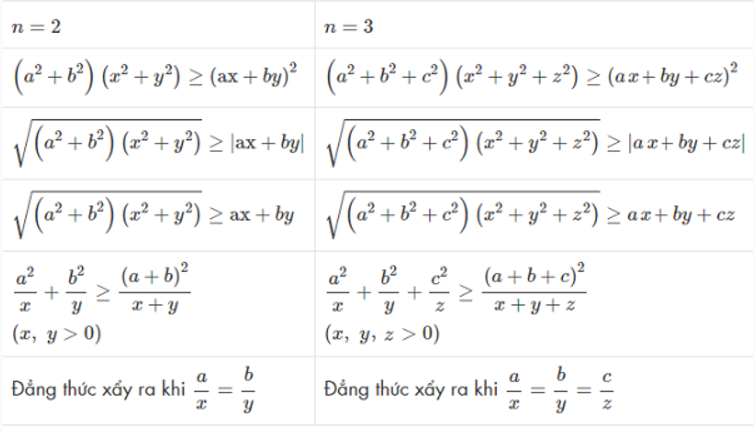
Khi gặp các bài toán có tham số, nên chia thành các trường hợp và xét dấu của biểu thức theo từng khoảng giá trị của tham số. Phương pháp này giúp giải quyết triệt để các bài toán phức tạp.

So sánh bất đẳng thức Bunhiacopxki với các bất đẳng thức cơ bản khác

Bất đẳng thức Bunhiacopxki có nhiều điểm tương đồng và khác biệt so với các bất đẳng thức cơ bản khác trong toán học. Về bản chất, nó là một công cụ mạnh mẽ để chứng minh các bất đẳng thức liên quan đến tổng và tích của các số thực dương.

So với bất đẳng thức Cauchy-Schwarz, định lý Bunhiacopxki có ưu thế hơn khi xử lý các bài toán liên quan đến dãy số có tính chất đặc biệt. Đặc biệt trong trường hợp các số hạng có mối liên hệ phức tạp, bất đẳng thức này thường cho kết quả chính xác và dễ áp dụng hơn.

Khi so sánh với bất đẳng thức AM-GM, bất đẳng thức BCS thể hiện tính linh hoạt cao hơn bởi khả năng xử lý các biểu thức có dạng tổng quát phức tạp. Điều này giúp giải quyết hiệu quả nhiều bài toán tối ưu trong đại số và giải tích.

Mối liên hệ với bất đẳng thức Cauchy

Bất đẳng thức Bunhiacopxki và Cauchy có mối liên hệ chặt chẽ trong việc chứng minh các bất đẳng thức. Trong nhiều trường hợp, chúng có thể được sử dụng thay thế cho nhau để đạt được kết quả mong muốn.

Khi áp dụng vào các bài toán cụ thể, hai bất đẳng thức này thường bổ trợ cho nhau. Nếu một bài toán khó giải quyết bằng bất đẳng thức Cauchy, việc chuyển sang sử dụng Bunhiacopxki có thể mang lại hướng tiếp cận mới hiệu quả hơn.

Sự kết hợp giữa hai bất đẳng thức tạo nên công cụ mạnh mẽ trong việc giải quyết các bài toán phức tạp. Đây là lý do các chuyên gia toán học thường xem xét cả hai phương pháp này song song khi tiếp cận vấn đề.

Ưu điểm và hạn chế khi sử dụng

Về ưu điểm, bất đẳng thức Bunhiacopxki cho phép xử lý hiệu quả các bài toán có cấu trúc phức tạp, đặc biệt là những bài toán liên quan đến tổng và tích của nhiều biến số. Phương pháp này cũng giúp đơn giản hóa quá trình chứng minh trong nhiều trường hợp.

Tuy nhiên, bất đẳng thức này cũng tồn tại một số hạn chế đáng kể. Việc áp dụng đòi hỏi người học phải có kiến thức nền tảng vững chắc về đại số và kỹ năng phân tích bài toán tốt. Ngoài ra, trong một số trường hợp đặc biệt, việc sử dụng bất đẳng thức này có thể dẫn đến các phép tính phức tạp không cần thiết.

Để khắc phục những hạn chế này, người học cần thực hành nhiều và phát triển khả năng nhận diện các tình huống phù hợp để áp dụng bất đẳng thức. Việc kết hợp linh hoạt với các phương pháp khác cũng là một chiến lược hiệu quả.

Các biến thể và dạng tổng quát của bất đẳng thức Bunhiacopxki

Bất đẳng thức bu-nhi-a-cốp-xki có nhiều dạng biến thể khác nhau, mỗi dạng đều có những đặc điểm và ứng dụng riêng trong việc giải toán. Dạng tổng quát phổ biến nhất là (a + b)² ≥ 4ab, với a và b là hai số thực dương bất kỳ. Đây được xem là nền tảng để phát triển các dạng phức tạp hơn.

Một biến thể quan trọng khác là dạng mở rộng cho n số thực dương, được biểu diễn dưới dạng (x₁ + x₂ + … + xₙ)² ≥ n(x₁x₂ + x₂x₃ + … + xₙx₁). Dạng này thường xuất hiện trong các bài toán tối ưu và chứng minh bất đẳng thức phức tạp.

Ngoài ra còn có dạng biến thể với các hàm số, trong đó công thức bunhiacopxki được áp dụng cho các biểu thức chứa hàm mũ, logarit hoặc lượng giác. Những dạng này đòi hỏi sự hiểu biết sâu sắc về tính chất của từng loại hàm số.

Các dạng biến đổi thường gặp

Trong thực tế giải toán, các dạng biến đổi của bất đẳng thức thường xuất hiện dưới nhiều hình thức khác nhau. Một trong những dạng phổ biến là biến đổi về cùng một biến số thông qua phép thế.

Việc áp dụng các phép biến đổi đồng dạng cũng là một kỹ thuật quan trọng. Bằng cách nhân cả hai vế với một số dương hoặc lấy nghịch đảo, ta có thể chuyển về dạng thuận lợi hơn để giải quyết.

Đặc biệt, khi kết hợp với các bất đẳng thức khác như Cauchy hay Jensen, bat dang thuc bunhiacopxki có thể được mở rộng thành những dạng phức tạp hơn, giúp giải quyết nhiều bài toán khó trong Olympic toán.

Phương pháp nhận biết và áp dụng

Để nhận biết khi nào cần sử dụng bất đẳng thức này, cần chú ý đến sự xuất hiện của các biểu thức bình phương và tích của các số dương. Khi bài toán yêu cầu chứng minh một bất đẳng thức có dạng tương tự, đây thường là dấu hiệu để áp dụng.

Trong quá trình giải toán, việc phân tích cấu trúc của biểu thức đóng vai trò quan trọng. Nếu có thể biến đổi về dạng tổng của các số hạng dương và tích của chúng, khả năng cao bất đẳng thức này sẽ được áp dụng.

Một chiến lược hiệu quả là kết hợp với các phương pháp khác như phương pháp quy nạp, phương pháp biến đổi tương đương hay phương pháp phản chứng. Điều này giúp mở rộng phạm vi ứng dụng và tăng hiệu quả giải quyết bài toán.

Bất đẳng thức Bunhiacopxki không chỉ là một trong những công cụ toán học quan trọng, mà còn mang lại nhiều lợi ích trong việc giải quyết bài toán ở nhiều cấp độ khác nhau. Việc nắm vững định lý này giúp học sinh có thêm khả năng áp dụng vào các bài tập thực tiễn và rèn luyện kĩ năng giải toán hiệu quả. Hãy cùng khám phá và vận dụng bất đẳng thức này để nâng cao thành tích học tập của bạn!