Tính chất đường phân giác trong tam giác và ứng dụng trong giải toán hình học

Tính chất đường phân giác là kiến thức quan trọng trong hình học. Đường phân giác không chỉ chia đôi góc của tam giác mà còn có nhiều ứng dụng trong việc giải các bài toán. Làm quen với những tính chất này sẽ giúp học sinh nắm vững và áp dụng vào thực tiễn một cách hiệu quả.

Tính chất đường phân giác trong tam giác và ứng dụng

Đường phân giác là đường thẳng chia đôi một góc thành hai góc bằng nhau. Trong tam giác, tính chất đường phân giác có vai trò quan trọng giúp giải quyết nhiều bài toán hình học phức tạp. Đặc biệt, nó có mối liên hệ chặt chẽ với tính chất phân phối trong các phép biến hình.

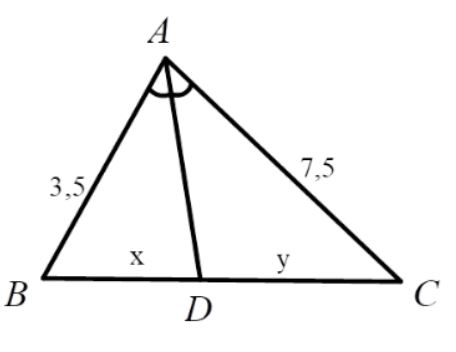
Khi xét về mặt hình học, đường phân giác của một góc trong tam giác sẽ chia cạnh đối diện thành hai phần tỷ lệ với độ dài hai cạnh kề góc đó. Điều này tạo nên một công cụ hữu hiệu để tính toán các yếu tố trong tam giác như độ dài cạnh, số đo góc hay diện tích các phần được chia.

Phân giác là một khái niệm cơ bản nhưng có nhiều ứng dụng thực tiễn. Trong kiến trúc, nguyên lý phân giác được áp dụng để thiết kế các cấu trúc đối xứng, tạo tính thẩm mỹ và cân bằng cho công trình. Trong quang học, định luật phản xạ ánh sáng cũng dựa trên nguyên lý về đường phân giác của góc tới và góc phản xạ.

Việc nắm vững các tính chất của đường phân giác không chỉ giúp giải quyết các bài toán hình học cơ bản mà còn là nền tảng để tiếp cận những vấn đề phức tạp hơn trong toán học và các lĩnh vực ứng dụng khác. Đây là một công cụ quan trọng trong việc phát triển tư duy logic và khả năng giải quyết vấn đề.

Các tính chất cơ bản của đường phân giác trong tam giác

Tính chất đường phân giác trong tam giác là những đặc điểm quan trọng giúp giải quyết nhiều bài toán hình học. Đường phân giác có vai trò đặc biệt trong việc chia đôi góc và tạo ra các tỷ lệ đặc trưng giữa các đoạn thẳng. Tính chất tia phân giác là nền tảng để hiểu rõ hơn về các tính chất này trong tam giác.

Đường phân giác chia đôi góc của tam giác

Đường phân giác của một góc trong tam giác là tia xuất phát từ đỉnh góc và chia góc đó thành hai góc bằng nhau. Tính chất này được áp dụng cho cả ba góc của tam giác, tạo thành ba đường phân giác nội tiếp.

Khi vẽ đường phân giác từ đỉnh A của tam giác ABC, ta sẽ tạo ra hai góc bằng nhau ở hai bên. Điều này có ý nghĩa quan trọng trong việc xác định tâm đường tròn nội tiếp của tam giác, vì ba đường phân giác của tam giác đồng quy tại một điểm.

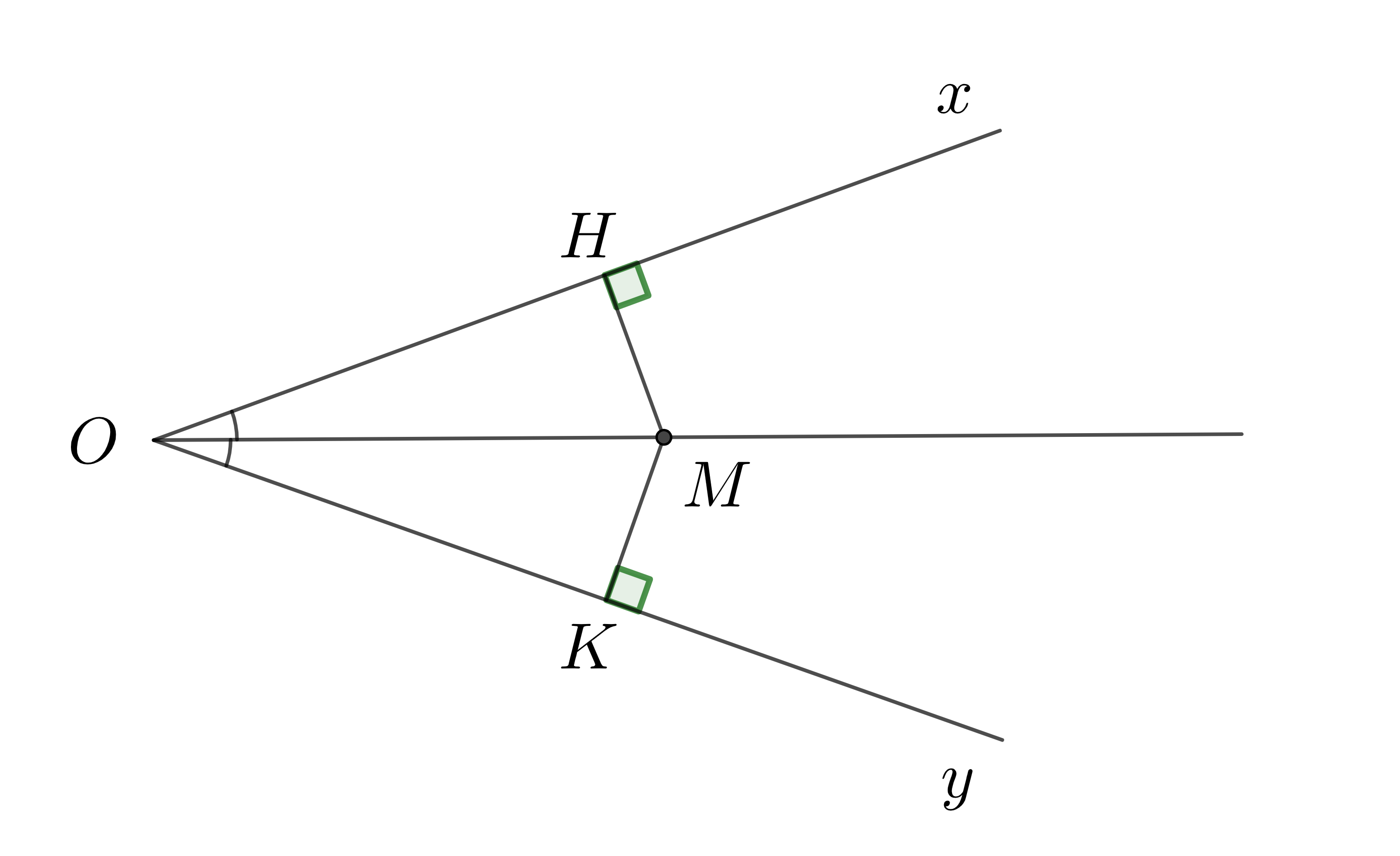
Tỷ lệ khoảng cách từ một điểm trên đường phân giác đến hai cạnh

Một điểm bất kỳ nằm trên đường phân giác của một góc sẽ cách đều hai cạnh của góc đó. Cụ thể, nếu M là một điểm trên đường phân giác của góc A, thì khoảng cách từ M đến hai cạnh AB và AC bằng nhau.

Tính chất này được ứng dụng rộng rãi trong việc xác định vị trí các điểm đặc biệt trong tam giác. Ví dụ, tâm đường tròn nội tiếp của tam giác là điểm cách đều ba cạnh của tam giác, do đó nó chính là giao điểm của ba đường phân giác.

Công thức tính độ dài đường phân giác

Độ dài đường phân giác trong tam giác được tính bằng công thức đặc biệt liên quan đến các cạnh của tam giác. Với đường phân giác AD của góc A trong tam giác ABC, độ dài AD được tính theo công thức:
AD = (2bc.cosA/2)/(b+c)

Trong đó:

• b và c là độ dài hai cạnh kề với góc A
• A là số đo của góc cần chia

Tính chất phân giác trong tam giác này giúp giải quyết nhiều bài toán phức tạp về tính toán độ dài và diện tích trong tam giác. Việc áp dụng công thức này đòi hỏi sự hiểu biết về các yếu tố trong tam giác và kỹ năng tính toán chính xác.

Đặc điểm của đường phân giác trong tam giác vuông

Tính chất đường phân giác trong tam giác vuông có những đặc điểm độc đáo và quan trọng. Đường phân giác góc vuông luôn tạo với hai cạnh góc vuông hai góc bằng nhau và bằng 45 độ. Điều này tạo nên tính đối xứng đặc biệt cho tam giác vuông.

Khi xét về độ dài, đường phân giác góc vuông chia cạnh huyền thành hai phần không bằng nhau. Phần gần cạnh lớn sẽ dài hơn phần gần cạnh nhỏ, tuân theo tỷ lệ nghịch với độ dài hai cạnh góc vuông. Điều này tạo ra mối liên hệ chặt chẽ với đường trung bình và các yếu tố khác trong tam giác.

Vị trí đường phân giác góc vuông

Đường phân giác góc vuông xuất phát từ đỉnh góc vuông và kéo dài đến cạnh huyền. Điểm giao của đường phân giác với cạnh huyền là điểm đặc biệt, nó chia cạnh huyền theo tỷ lệ bằng tỷ số độ dài hai cạnh góc vuông.

Vị trí này tạo ra hai tam giác nhỏ đồng dạng với tam giác ban đầu. Hai tam giác này có chung góc ở đỉnh góc vuông và có góc 45 độ tại giao điểm của đường phân giác với cạnh huyền.

Mối quan hệ với các yếu tố khác trong tam giác vuông

Tính chất đường pg trong tam giác vuông thể hiện mối liên hệ chặt chẽ với nhiều yếu tố hình học khác. Đường phân giác góc vuông tạo ra hai tam giác đồng dạng, có tỷ số các cạnh tương ứng bằng nhau và bằng tỷ số độ dài hai cạnh góc vuông ban đầu.

Độ dài đường phân giác góc vuông cũng có mối quan hệ đặc biệt với bán kính đường tròn nội tiếp tam giác. Cụ thể, độ dài đường phân giác góc vuông bằng tổng của bán kính đường tròn nội tiếp và khoảng cách từ tâm đường tròn nội tiếp đến cạnh huyền.

Ngoài ra, đường phân giác góc vuông còn là trung tuyến của tam giác được tạo bởi tâm đường tròn nội tiếp và hai điểm tiếp xúc trên hai cạnh góc vuông. Điều này tạo nên mối liên hệ đặc biệt giữa đường phân giác và đường tròn nội tiếp tam giác vuông.

Phương pháp chứng minh các bài toán về đường phân giác

Việc chứng minh các bài toán liên quan đến đường phân giác đòi hỏi nắm vững tính chất tia phân giác và các kiến thức hình học cơ bản. Đường phân giác của một góc là tập hợp các điểm nằm trong góc và cách đều hai cạnh của góc đó.

Để giải quyết các bài toán về đường phân giác, cần áp dụng định lý đường phân giác kết hợp với tính chất đường kính và dây cung trong tam giác. Việc vận dụng linh hoạt các tính chất này sẽ giúp giải quyết được nhiều dạng bài tập khác nhau.

Các bước chứng minh cơ bản

Khi tiếp cận bài toán về đường phân giác, cần thực hiện theo trình tự logic sau:

Bước 1: Xác định rõ giả thiết và kết luận cần chứng minh. Vẽ hình chính xác và đầy đủ các yếu tố.

Bước 2: Phân tích các tính chất của đường phân giác có thể áp dụng. Đặc biệt chú ý tỷ số các đoạn được chia bởi đường phân giác.

Bước 3: Thiết lập các mối quan hệ giữa các yếu tố trong hình vẽ, sử dụng các định lý và tính chất đã biết.

Ví dụ minh họa và bài tập áp dụng

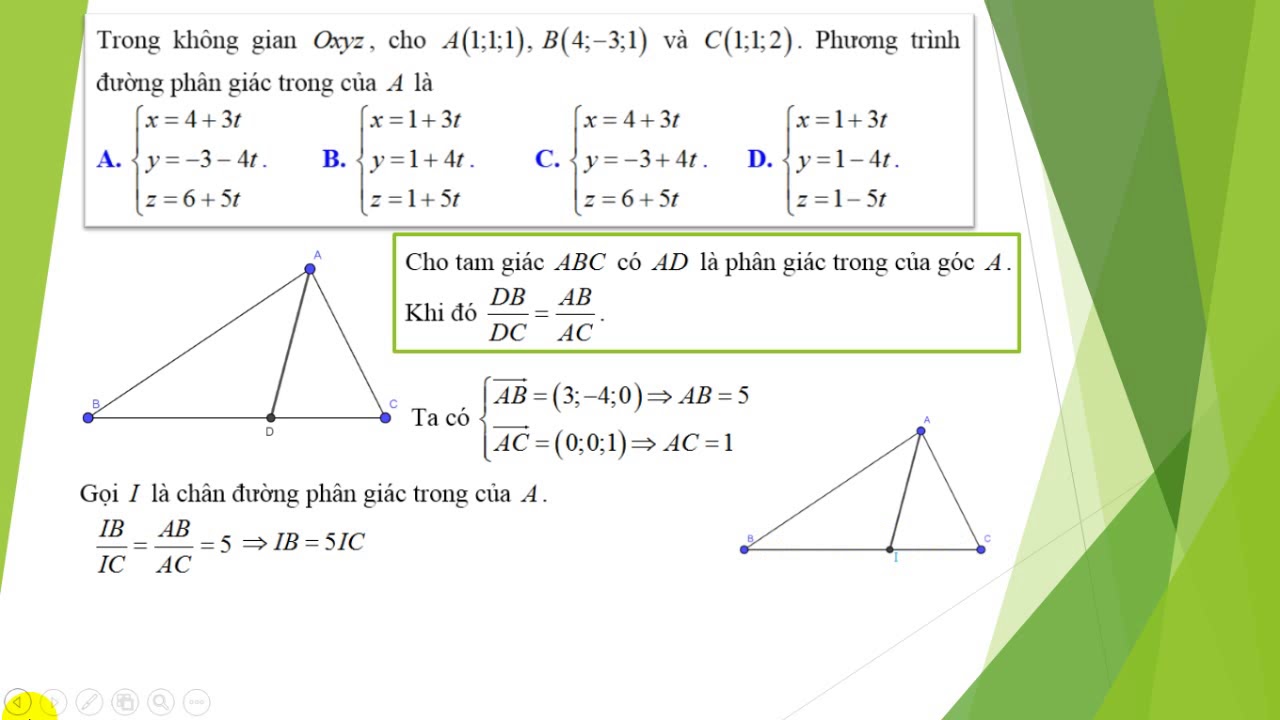
Ví dụ 1: Cho tam giác ABC có đường phân giác AD của góc A. Chứng minh rằng: AB/AC = BD/DC.

Lời giải:

• Vì AD là đường phân giác của góc A
• Lấy điểm M thuộc AD
• Kẻ các đường vuông góc từ M đến AB và AC
• Theo định nghĩa đường phân giác, các khoảng cách này bằng nhau
• Áp dụng định lý đường phân giác, ta có: AB/AC = BD/DC

Ví dụ 2: Cho tam giác ABC có đường phân giác AD. Điểm E thuộc AD sao cho AE = ED. Chứng minh BE = EC.

Qua các ví dụ trên, có thể thấy việc vận dụng các tính chất của đường phân giác kết hợp với các kiến thức hình học cơ bản sẽ giúp giải quyết được nhiều dạng bài tập phức tạp.

Ứng dụng của tính chất đường phân giác trong giải toán hình học

Tính chất đường phân giác có vai trò quan trọng trong việc giải các bài toán hình học. Đây là công cụ hữu hiệu giúp chứng minh các mối quan hệ về độ dài, góc và diện tích trong tam giác. Để áp dụng hiệu quả, cần nắm vững các tính chất cơ bản và phương pháp vận dụng phù hợp với từng dạng bài toán.

Bài toán tính độ dài đoạn thẳng

Khi giải bài toán tính độ dài đoạn thẳng, việc áp dụng tính chất đường phân giác ngoài giúp thiết lập các phương trình về tỷ số độ dài. Từ đó có thể tìm ra độ dài các cạnh, đường cao hay đường trung tuyến trong tam giác.

Phương pháp này đặc biệt hiệu quả khi cần tìm độ dài các đoạn thẳng được tạo bởi giao điểm của đường phân giác với các cạnh tam giác. Việc áp dụng tính chất về tỷ số các đoạn thẳng sẽ giúp đơn giản hóa quá trình tính toán.

Bài toán chứng minh tính chất

Trong các bài toán chứng minh, đường phân giác thường được sử dụng như một công cụ trung gian để thiết lập mối liên hệ giữa các yếu tố trong hình. Bằng cách kết hợp với các kiến thức về tam giác đồng dạng và tam giác cân, ta có thể chứng minh được nhiều tính chất hình học phức tạp.

Việc vận dụng linh hoạt các tính chất của đường phân giác kết hợp với các định lý về góc, cạnh trong tam giác sẽ mở ra nhiều hướng tiếp cận khác nhau cho bài toán. Điều này giúp tìm ra lời giải ngắn gọn và sáng tạo nhất.

Bài toán dựng hình học

Khi thực hiện các bài toán dựng hình, Học Thế Nào khuyến nghị sử dụng tính chất của đường phân giác như một công cụ dựng cơ bản. Phương pháp này cho phép xác định chính xác vị trí các điểm đặc biệt và dựng được các yếu tố phức tạp trong hình học.

Việc dựng đường phân giác thường là bước đệm quan trọng để tiếp tục dựng các yếu tố khác trong bài toán. Kết hợp với các phép dựng cơ bản như dựng đường vuông góc, dựng đường thẳng song song sẽ giúp hoàn thành bài toán một cách chính xác và hiệu quả.

Tính chất đường phân giác là một khái niệm quan trọng trong hình học, có ảnh hưởng sâu sắc đến việc giải quyết các bài toán liên quan đến tam giác. Qua bài viết, bạn đã khám phá những tính chất cơ bản của đường phân giác, vị trí và mối quan hệ trong tam giác vuông, cùng với các phương pháp chứng minh và ứng dụng trong các bài toán thực tế. Nắm vững những kiến thức này không chỉ giúp bạn cải thiện kỹ năng giải toán hình học mà còn mở rộng hiểu biết về các yếu tố hình học khác.