Tính chất phân phối và ứng dụng trong toán học cơ bản cho học sinh

Tính chất phân phối là một khái niệm quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về quan hệ giữa các phép toán. Bài viết này sẽ giới thiệu về các dạng tính chất phân phối, quy luật phân phối và ứng dụng thực tế của chúng. Hãy cùng khám phá cách tính toán nhanh và giải bài tập hiệu quả qua các công thức chính xác.

Tính chất phân phối trong toán học và ứng dụng cơ bản

Tính chất phân phối là một trong những quy tắc quan trọng trong đại số sơ cấp, giúp chúng ta thực hiện các phép tính số học một cách linh hoạt và hiệu quả. Quy tắc này cho phép phân tách một phép nhân với tổng thành tổng của các phép nhân riêng lẻ.

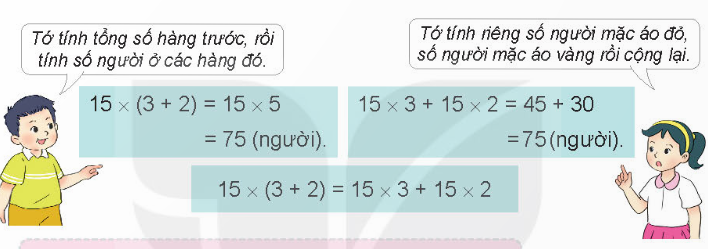
Khi áp dụng nhân phân phối, ta có thể viết a(b + c) = ab + ac. Điều này có nghĩa là khi một số nhân với một tổng, kết quả sẽ bằng tổng của các tích khi số đó nhân với từng số hạng. Ví dụ: 2(3 + 4) = 2×3 + 2×4 = 6 + 8 = 14.

Tính chất này không chỉ đúng với các số nguyên mà còn đúng với phân số, số thập phân và biểu thức đại số. Nó là nền tảng cho nhiều phương pháp tính toán nâng cao như khai triển đa thức, phân tích nhân tử và giải phương trình. Trong thực tế, tính chất phân phối giúp đơn giản hóa các phép tính phức tạp và là công cụ thiết yếu trong việc kiểm tra kết quả tính toán.

Các dạng tính chất phân phối thường gặp trong phép tính số học

Tính chất phân phối là một trong những quy tắc quan trọng trong phép tính số học, cho phép phân tích một phép nhân với tổng hoặc hiệu thành tổng hoặc hiệu của các phép nhân. Tính chất này giúp đơn giản hóa các phép tính phức tạp và tạo điều kiện thuận lợi cho việc tính toán nhanh.

Có hai dạng tính chất phân phối chính thường được áp dụng trong toán học. Đó là tính chất phân phối của phép nhân đối với phép cộng và tính chất phân phối của phép nhân đối với phép trừ. Mỗi dạng đều có những đặc điểm và cách áp dụng riêng biệt.

Tính chất phân phối của phép nhân đối với phép cộng

Tính chất này thể hiện qua công thức: a × (b + c) = (a × b) + (a × c). Khi một số nhân với tổng của hai số, kết quả bằng tổng của hai tích khi số đó nhân với từng số hạng.

Ví dụ thực tế từ giáo viên toán Nguyễn Thị Mai (Trường THCS Lê Quý Đôn): “Khi dạy học sinh tính 7 × (8 + 5), thay vì cộng 8 và 5 trước rồi nhân với 7, các em có thể áp dụng tính chất phân phối để tính: 7 × 8 + 7 × 5 = 56 + 35 = 91”.

Tính chất phân phối của phép nhân đối với phép trừ

Tương tự như tính chất đường phân giác của tam giác, tính chất phân phối của phép nhân đối với phép trừ cũng có quy tắc riêng. Công thức thể hiện: a × (b – c) = (a × b) – (a × c).

Khi một số nhân với hiệu của hai số, kết quả bằng hiệu của hai tích khi số đó nhân với số bị trừ và số trừ. Điều này tạo ra sự linh hoạt trong cách tiếp cận các bài toán phức tạp.

Ứng dụng tính chất phân phối trong tính toán nhanh

Tính chất phân phối mang lại nhiều lợi ích trong việc tính toán nhanh, đặc biệt với các số có nhiều chữ số. Phương pháp này giúp chia nhỏ bài toán thành các phép tính đơn giản hơn.

Một ví dụ điển hình là phép nhân với 99: 99 × 245 có thể được tính bằng cách: (100 – 1) × 245 = 100 × 245 – 1 × 245 = 24.500 – 245 = 24.255. Cách này nhanh hơn nhiều so với phép nhân thông thường.

Trong thực tế, các nhà toán học thường kết hợp tính chất phân phối với các phương pháp khác để tạo ra những cách tính nhanh và hiệu quả. Điều này đặc biệt hữu ích trong các bài toán thi đấu hoặc tính toán thương mại.

Phân phối xác suất và các quy luật cơ bản trong thống kê

Trong thống kê, quy luật phân phối đóng vai trò nền tảng để mô tả và phân tích dữ liệu. Các quy luật này giúp các nhà nghiên cứu hiểu được cách thức phân bố của các biến số và dự đoán xác suất xảy ra của các sự kiện.

Việc nắm vững các quy luật phân phối giúp đưa ra những kết luận chính xác trong nghiên cứu thống kê, tương tự như cách đường phân giác là gì giúp chia đôi một góc trong hình học. Phân phối xác suất là công cụ quan trọng để mô tả mối quan hệ giữa các biến số ngẫu nhiên.

Khái niệm về phân phối xác suất

Phân phối xác suất là một mô hình toán học mô tả xác suất xảy ra của tất cả các giá trị có thể có của một biến ngẫu nhiên. Nó cho biết mỗi kết quả có thể xảy ra với xác suất bao nhiêu.

Trong thực tế, phân phối xác suất thường được biểu diễn dưới dạng hàm mật độ xác suất (PDF) đối với biến liên tục hoặc hàm khối xác suất (PMF) đối với biến rời rạc. Các hàm này tuân theo các tính chất cơ bản như tổng xác suất bằng 1 và xác suất không âm.

Các dạng phân phối xác suất phổ biến

Có nhiều dạng phân phối xác suất khác nhau, mỗi dạng phù hợp với những loại dữ liệu và tình huống cụ thể. Việc lựa chọn phân phối phù hợp là bước quan trọng trong phân tích thống kê.

Phân phối chuẩn và đặc điểm

Phân phối chuẩn là một trong những phân phối quan trọng nhất trong thống kê. Đường cong phân phối có dạng hình chuông đối xứng, với giá trị trung bình, trung vị và mode trùng nhau tại đỉnh.

Theo nghiên cứu của Karl Pearson, khoảng 68% dữ liệu nằm trong khoảng một độ lệch chuẩn so với giá trị trung bình, 95% trong khoảng hai độ lệch chuẩn và 99.7% trong khoảng ba độ lệch chuẩn.

Phân phối nhị thức và ứng dụng

Phân phối nhị phân mô tả xác suất thành công trong một chuỗi các phép thử độc lập, với mỗi phép thử chỉ có hai kết quả có thể xảy ra. Ví dụ như tung đồng xu hay kết quả đậu/rớt trong một kỳ thi.

Trong lĩnh vực kiểm soát chất lượng, các công ty như Toyota sử dụng phân phối nhị thức để đánh giá tỷ lệ sản phẩm lỗi trong dây chuyền sản xuất. Điều này giúp họ duy trì tiêu chuẩn chất lượng và cải thiện quy trình sản xuất liên tục.

Phân phối rời rạc và ứng dụng trong bài toán thực tế

Phân phối rời rạc là một khái niệm thống kê quan trọng mô tả các biến ngẫu nhiên chỉ nhận các giá trị rời rạc. Trong thực tế, phân phối này thường xuất hiện khi đếm số lượng sự kiện hoặc đối tượng rời rạc như số khách hàng, số sản phẩm lỗi hay số lần xảy ra một hiện tượng.

Việc hiểu và áp dụng phân phối rời rạc giúp các nhà phân tích dữ liệu đưa ra những dự đoán chính xác về các hiện tượng trong tự nhiên và xã hội. Tương tự như tính chất hình chiếu, phân phối rời rạc có những đặc điểm và quy luật riêng cần nắm vững để ứng dụng hiệu quả.

Đặc điểm của phân phối rời rạc

Phân phối rời rạc có đặc điểm cơ bản là biến ngẫu nhiên chỉ nhận các giá trị riêng biệt, không liên tục. Điều này tạo nên sự khác biệt so với phân phối liên tục, nơi biến số có thể nhận mọi giá trị trong một khoảng.

Một đặc điểm quan trọng khác là tổng xác suất của tất cả các giá trị có thể xảy ra luôn bằng 1. Điều này đảm bảo tính chất cơ bản của lý thuyết xác suất và cho phép các nhà nghiên cứu tính toán chính xác khả năng xảy ra của các sự kiện.

Ngoài ra, phân phối rời rạc thường được biểu diễn bằng hàm khối xác suất thay vì hàm mật độ xác suất như trong phân phối liên tục. Điều này giúp việc tính toán và phân tích trở nên đơn giản và trực quan hơn.

Các bài toán thường gặp về phân phối rời rạc

Trong lĩnh vực kiểm soát chất lượng sản phẩm, các công ty thường sử dụng phân phối rời rạc để phân tích số lượng sản phẩm lỗi trong một lô hàng. Ví dụ, công ty Samsung đã áp dụng phân phối này để kiểm soát tỷ lệ lỗi trong quy trình sản xuất điện thoại di động, giúp cải thiện chất lượng sản phẩm và giảm chi phí sản xuất.

Trong ngành bảo hiểm, các công ty sử dụng phân phối rời rạc để dự đoán số lượng yêu cầu bồi thường trong một khoảng thời gian nhất định. Điều này giúp họ xác định mức phí bảo hiểm phù hợp và duy trì khả năng thanh toán.

Các ngân hàng cũng áp dụng phân phối rời rạc để phân tích số lượng giao dịch tại ATM hoặc số lượng khách hàng đến giao dịch trực tiếp. Từ đó, họ có thể tối ưu hóa việc bố trí nhân sự và quản lý dòng tiền hiệu quả hơn.

Lý thuyết phân phối và các công thức tính toán quan trọng

Lý thuyết phân phối là nền tảng quan trọng trong thống kê và xác suất, giúp mô tả quy luật phân bố của các biến ngẫu nhiên. Các phân phối thống kê phổ biến bao gồm phân phối chuẩn, phân phối Poisson và phân phối nhị thức, mỗi loại đều có những đặc điểm và ứng dụng riêng.

Việc hiểu rõ các tính chất phân phối giúp chúng ta có thể áp dụng chính xác vào từng bài toán cụ thể. Ví dụ, phân phối chuẩn thường được sử dụng để mô tả các hiện tượng tự nhiên như chiều cao, cân nặng của người trong một quần thể, trong khi phân phối Poisson phù hợp với việc mô tả số sự kiện hiếm gặp trong một khoảng thời gian.

Các công thức cơ bản trong lý thuyết phân phối

Công thức hàm mật độ xác suất của phân phối chuẩn:
f(x) = (1/σ√2π) * e^(-(x-μ)²/2σ²)
Trong đó μ là kỳ vọng và σ là độ lệch chuẩn của phân phối.

Đối với phân phối Poisson, xác suất xảy ra k sự kiện được tính theo công thức:
P(X = k) = (λ^k * e^-λ)/k!
Với λ là tham số của phân phối, biểu thị số sự kiện trung bình trong một đơn vị thời gian.

Phương pháp giải bài tập về phân phối

Bước đầu tiên khi giải bài tập về phân phối là xác định chính xác loại phân phối phù hợp với bài toán. Điều này đòi hỏi phải nắm vững đặc điểm của từng loại phân phối và điều kiện áp dụng của chúng.

Sau khi xác định được loại phân phối, cần tìm các tham số đặc trưng như kỳ vọng, phương sai hoặc độ lệch chuẩn. Những giá trị này sẽ được thay vào công thức tương ứng để tính toán xác suất hoặc các đại lượng cần tìm.

Một ví dụ thực tế từ nghiên cứu của Đại học Stanford cho thấy việc áp dụng phân phối chuẩn trong phân tích điểm số của sinh viên giúp đánh giá chính xác hơn về năng lực học tập và có những điều chỉnh phù hợp trong phương pháp giảng dạy.

Tính chất phân phối đóng vai trò quan trọng trong toán học, giúp đơn giản hóa nhiều phép tính. Các kiến thức về tính chất phân phối trong phép nhân, các loại phân phối xác suất và phân phối rời rạc không chỉ giúp học sinh dễ dàng tiếp cận lý thuyết mà còn ứng dụng hiệu quả trong giải bài tập thực tế. Bằng cách hiểu rõ các tính chất căn bản này, người học có thể nâng cao khả năng giải toán của mình.