Đường trung bình trong hình học: Công thức, tính chất và ứng dụng thực tế

Đường trung bình là một khái niệm quan trọng trong hình học phẳng. Đoạn thẳng này không chỉ liên kết giữa hai cạnh đối diện mà còn thể hiện nhiều tính chất độc đáo. Bài viết sẽ khám phá chi tiết về tính chất, công thức và ứng dụng của đường trung bình trong toán học. Hãy cùng bắt đầu hành trình tìm hiểu thú vị này!

Đường trung bình là đoạn thẳng song song và bằng nửa hai cạnh đối diện trong hình học phẳng

Trong hình học phẳng oxy, đường trung bình là một khái niệm quan trọng giúp giải quyết nhiều bài toán hình học. Đây là đoạn thẳng nối hai điểm chính giữa của hai cạnh bất kỳ trong tam giác hoặc hình thang.

Khi nghiên cứu về đường trung bình là gì, ta cần hiểu rõ tính chất cơ bản: đường trung bình luôn song song với cạnh còn lại và có độ dài bằng một nửa cạnh đó. Tính chất này được áp dụng cho cả tam giác và hình thang, tạo nên mối liên hệ chặt chẽ giữa các yếu tố trong hình.

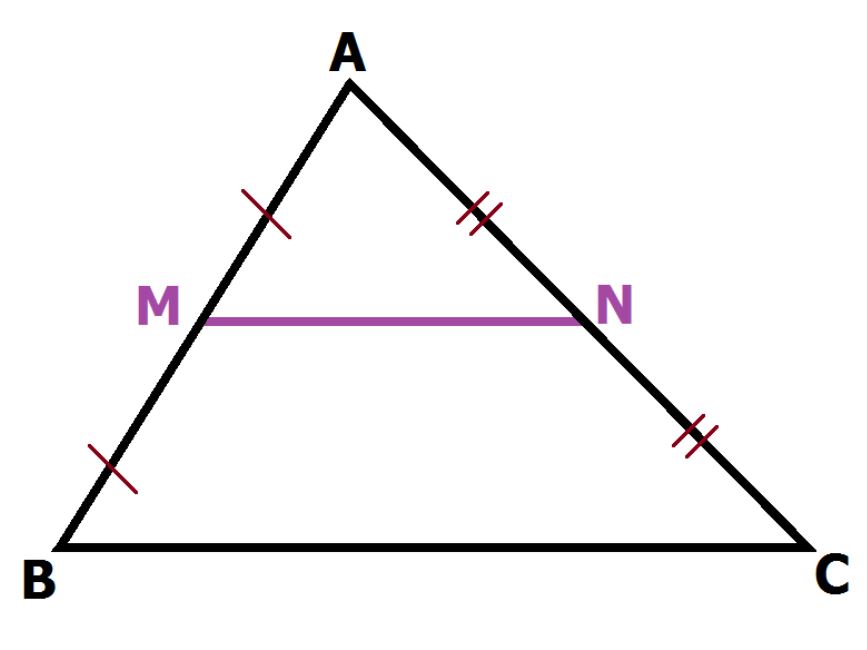
Đường trung bình có vai trò đặc biệt trong việc chia đôi diện tích hình. Ví dụ trong tam giác, đường trung bình chia tam giác thành hai phần có diện tích bằng nhau. Điều này giúp đơn giản hóa nhiều bài toán tính diện tích phức tạp và tạo cơ sở cho việc chứng minh các định lý hình học nâng cao.

Các tính chất quan trọng của đường trung bình trong hình học phẳng

Tính chất đường trung bình trong toán học đóng vai trò quan trọng giúp giải quyết nhiều bài toán hình học phức tạp. Đường trung bình có những đặc điểm độc đáo về vị trí và tỷ lệ, tạo nên mối liên hệ chặt chẽ giữa các yếu tố trong hình học.

Để hiểu rõ hơn về đường trung bình, cần nắm vững các tính chất cơ bản và ứng dụng của nó trong các hình học phẳng phổ biến. Điều này giúp việc giải toán trở nên dễ dàng và hiệu quả hơn.

Tính chất song song và tỷ lệ độ dài của đường trung bình

Đường trung bình luôn song song với cạnh đáy và có độ dài bằng một nửa độ dài cạnh đáy. Tính chất này được áp dụng phổ biến trong tam giác và hình thang, tạo nên mối quan hệ tỷ lệ đặc biệt giữa các thành phần.

Trong thực tế, các kiến trúc sư thường áp dụng nguyên lý này khi thiết kế các công trình có cấu trúc đối xứng. Ví dụ như Nhà hát Opera Sydney sử dụng tỷ lệ đường trung bình để tạo nên những đường cong hài hòa và cân đối.

Đặc điểm vị trí của đường trung bình trong các hình học cơ bản

Vị trí của đường trung bình có mối liên hệ mật thiết với tính chất 3 đường cao trong các hình học phẳng. Sự kết hợp này tạo nên những tính chất đặc biệt giúp giải quyết nhiều bài toán phức tạp.

Vị trí đường trung bình trong tam giác

Trong tam giác, đường trung bình nối trung điểm hai cạnh tạo thành một tam giác nhỏ có diện tích bằng một phần tư tam giác ban đầu. Đặc điểm này được ứng dụng rộng rãi trong việc tính toán diện tích và thiết kế các cấu trúc hình học.

Các nhà toán học đã chứng minh rằng đường trung bình chia tam giác thành các phần có tỷ lệ cố định. Điều này tạo nên một công cụ hữu ích trong việc phân chia diện tích và xác định vị trí các điểm đặc biệt.

Vị trí đường trung bình trong hình thang

Trong hình thang, đường trung bình có vai trò đặc biệt khi nó song song với hai đáy và có độ dài bằng trung bình cộng của hai đáy. Tính chất này được ứng dụng nhiều trong thiết kế công nghiệp và xây dựng.

Các kỹ sư cơ khí thường sử dụng nguyên lý này khi thiết kế các chi tiết máy có dạng hình thang. Ví dụ như trong thiết kế bánh răng côn, vị trí đường trung bình giúp xác định chính xác điểm tiếp xúc và góc nghiêng tối ưu.

Phương pháp xác định và tính toán đường trung bình trong các hình học phẳng

Đường trung bình là một yếu tố quan trọng trong hình học phẳng, giúp xác định các đặc điểm và tính chất của hình. Công thức đường trung bình được áp dụng khác nhau tùy thuộc vào từng loại hình học cụ thể.

Để tính đường trung bình chính xác, cần nắm vững các khái niệm cơ bản về đường trung trực là đường gì và đặc điểm của từng hình. Cách tính đường trung bình sẽ được trình bày chi tiết cho từng trường hợp dưới đây.

Công thức tính đường trung bình trong tam giác

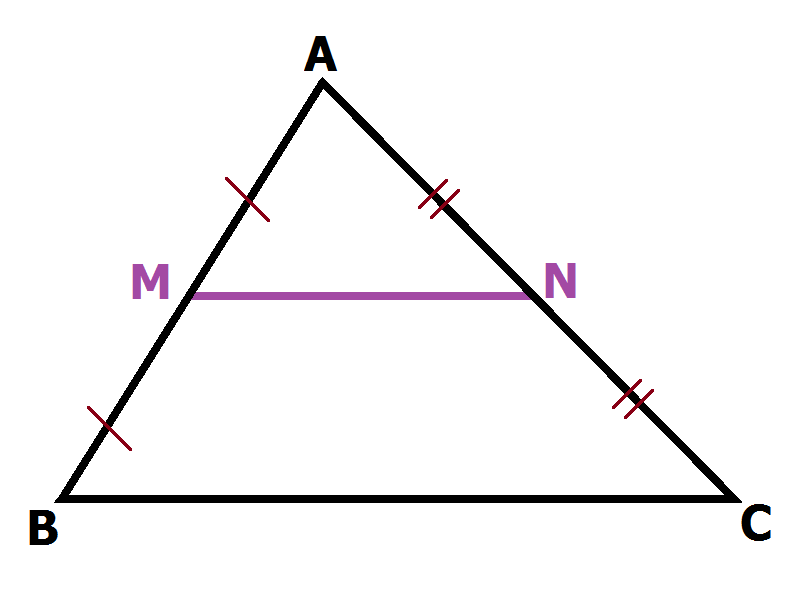
Đường trung bình trong tam giác là đoạn thẳng nối trung điểm của hai cạnh. Mỗi tam giác có 3 đường trung bình, song song với cạnh còn lại và bằng một nửa độ dài cạnh đó.

Nếu gọi M, N lần lượt là trung điểm của hai cạnh AB và AC, thì MN là đường trung bình và có công thức: MN = 1/2 BC. Tương tự, với các cặp trung điểm khác sẽ tạo thành các đường trung bình còn lại.

Công thức tính đường trung bình trong hình thang

Đường trung bình trong hình thang là đoạn thẳng nối trung điểm của hai cạnh bên. Độ dài đường trung bình bằng nửa tổng độ dài hai đáy.

Với a, b là độ dài hai đáy của hình thang, công thức tính đường trung bình h = (a + b)/2. Đường trung bình chia hình thang thành hai phần có diện tích bằng nhau và song song với hai đáy.

Công thức tính đường trung bình trong hình bình hành

Trong hình bình hành, đường trung bình được xác định bằng đoạn thẳng nối trung điểm của hai cạnh đối diện. Mỗi hình bình hành có hai đường trung bình.

Đường trung bình trong hình bình hành có tính chất đặc biệt: chúng cắt nhau tại trung điểm và chia nhau thành hai phần bằng nhau. Độ dài mỗi đường trung bình bằng một nửa tổng độ dài hai cạnh kề nó.

Chứng minh các tính chất của đường trung bình trong hình học

Đường trung bình là một khái niệm quan trọng trong hình học, thường xuất hiện trong các bài toán về tam giác và hình thang. Chứng minh đường trung bình của tam giác giúp ta hiểu rõ các tính chất cơ bản và ứng dụng trong việc giải các bài toán phức tạp hơn.

Việc chứng minh các tính chất của đường trung bình có ý nghĩa quan trọng trong việc nghiên cứu các đường cong toán học như đường hypebol. Các tính chất này tạo nền tảng cho nhiều ứng dụng thực tiễn trong kiến trúc và kỹ thuật.

Chứng minh đường trung bình trong tam giác

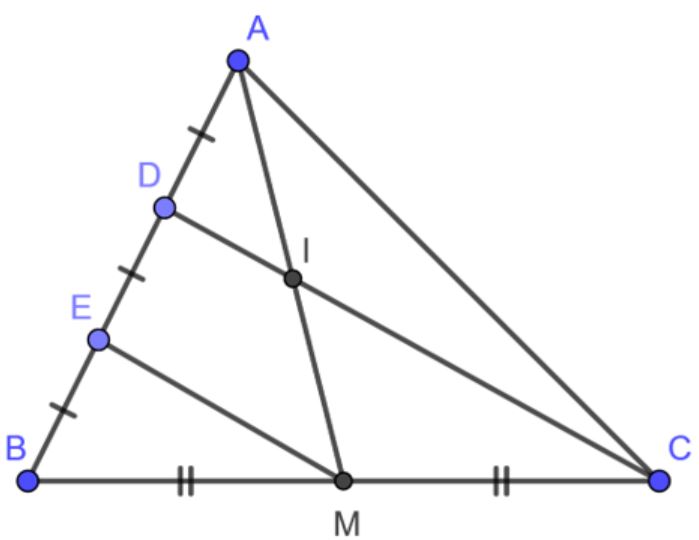
Để chứng minh tính chất của đường trung bình trong tam giác, ta cần xét tam giác ABC với D, E lần lượt là trung điểm của BC và AC. Khi đó DE là đường trung bình của tam giác ABC.

Theo định lý về đường trung bình, DE song song với AB và có độ dài bằng một nửa độ dài AB. Điều này được chứng minh bằng cách vẽ đường thẳng DE’ song song với AB qua điểm D, trong đó E’ nằm trên AC.

Do D là trung điểm của BC và các đường thẳng song song tạo ra các đoạn tương ứng tỷ lệ với nhau, nên E’ trùng với E – trung điểm của AC. Từ đó ta kết luận DE là đường trung bình của tam giác ABC.

Chứng minh đường trung bình trong hình thang

Trong hình thang ABCD với AB song song CD, gọi M, N lần lượt là trung điểm của AD và BC. Đoạn thẳng MN được gọi là đường trung bình của hình thang.

Để chứng minh tính chất của đường trung bình hình thang, ta kẻ đường chéo AC. Khi đó hình thang được chia thành hai tam giác ABC và ADC. Theo tính chất đường trung bình trong tam giác, MN song song với AB và CD.

Độ dài của đường trung bình MN bằng trung bình cộng của hai đáy AB và CD. Điều này được chứng minh thông qua việc áp dụng định lý về tỷ số của các đoạn thẳng song song cắt bởi các đường xiên.

Ứng dụng của đường trung bình trong thực tế và bài toán

Ứng dụng đường trung bình có vai trò quan trọng trong nhiều lĩnh vực từ toán học thuần túy đến các ứng dụng thực tiễn. Đường trung bình giúp đơn giản hóa các phép tính phức tạp và mang lại cái nhìn tổng quan về dữ liệu. Theo Học Thế Nào VN, việc áp dụng đường trung bình còn giúp tối ưu hóa nhiều quy trình trong sản xuất và nghiên cứu.

Ứng dụng trong các bài toán hình học phẳng

Trong hình học phẳng, đường trung bình đóng vai trò then chốt khi giải quyết các bài toán về diện tích và chu vi. Đường trung bình của tam giác cho phép tính nhanh diện tích hình thang mà không cần sử dụng công thức phức tạp.

Khi xử lý các bài toán về hình học không gian, đường trung bình giúp xác định tâm đối xứng và tính toán khoảng cách giữa các điểm. Phương pháp này đặc biệt hữu ích trong thiết kế kiến trúc và quy hoạch không gian.

Ứng dụng trong thống kê và đo lường

Đường trung bình trong thống kê được sử dụng rộng rãi để phân tích xu hướng dữ liệu. Trong nghiên cứu thị trường, các chuyên gia marketing thường dùng đường trung bình động để theo dõi biến động giá cả và hành vi người tiêu dùng.

Trong lĩnh vực đo lường công nghiệp, đường trung bình giúp kiểm soát chất lượng sản phẩm. Các nhà máy sử dụng biểu đồ kiểm soát với đường trung bình để phát hiện sai lệch trong quy trình sản xuất.

Ví dụ minh họa về ứng dụng đường trung bình

Một ví dụ về đường trung bình điển hình là trong ngành khí tượng thủy văn. Các trạm quan trắc sử dụng đường trung bình nhiệt độ 10 ngày để dự báo xu hướng thời tiết. Phương pháp này cho độ chính xác cao hơn so với đo đạc đơn lẻ.

Trong ngành tài chính, các nhà đầu tư chứng khoán sử dụng đường trung bình động 50 ngày và 200 ngày để xác định xu hướng thị trường. Khi đường giá cắt lên trên đường trung bình, đó thường là tín hiệu tăng giá và ngược lại.

Các công ty bán lẻ áp dụng đường trung bình để tối ưu hóa hàng tồn kho. Bằng cách theo dõi mức tiêu thụ trung bình trong 3 tháng, họ có thể dự đoán chính xác nhu cầu và điều chỉnh đơn hàng phù hợp.

Đường trung bình là đoạn thẳng đặc biệt trong hình học, mang lại nhiều ứng dụng hữu ích trong việc giải quyết bài toán. Các tính chất của đường trung bình, như tính song song và tỷ lệ độ dài, không chỉ giúp học sinh hiểu sâu mà còn kích thích khả năng tư duy. Nắm vững công thức và phương pháp chứng minh liên quan đến đường trung bình sẽ nâng cao khả năng giải toán ở mọi cấp độ.