Tính góc tam giác vuông: công thức, cách tính và ứng dụng trong toán học

Tính góc tam giác vuông là một phần quan trọng trong chương trình toán học. Việc nắm vững các công thức và phương pháp tính toán góc sẽ giúp học sinh giải quyết bài toán hiệu quả. Hãy cùng khám phá những công cụ cần thiết để bạn tự tin hơn trong môn học này.

Tính góc tam giác vuông và các phương pháp cơ bản

Để tính góc tam giác vuông, cần áp dụng các tỷ số lượng giác cơ bản như sin, cos, tan và các công thức hình học phẳng. Các góc trong tam giác vuông có mối quan hệ chặt chẽ với nhau, trong đó một góc luôn bằng 90 độ và tổng ba góc bằng 180 độ.

Phương pháp tính góc của tam giác vuông dựa trên việc xác định tỷ số giữa các cạnh. Khi biết độ dài hai cạnh bất kỳ, có thể sử dụng các hàm lượng giác nghịch đảo arcsin, arccos, arctan để tìm góc. Ví dụ, nếu biết cạnh đối và tính cạnh huyền tam giác vuông, góc được tính bằng arcsin của tỷ số giữa cạnh đối và cạnh huyền.

Một cách tiếp cận khác là sử dụng định lý Pythagore kết hợp với các tỷ số lượng giác. Khi đã xác định được một góc, góc còn lại sẽ bằng 90 độ trừ đi góc đã tìm được. Phương pháp này đặc biệt hữu ích khi chỉ biết độ dài của hai cạnh góc vuông hoặc một cạnh góc vuông và cạnh huyền.

Các công thức tính góc trong tam giác vuông thông dụng

Để tính chính xác các công thức tính góc trong tam giác vuông, cần nắm vững các phương pháp tính dựa trên tỷ số lượng giác, định lý Pythagore và tính chất đường cao. Mỗi phương pháp có những ưu điểm riêng và phù hợp với từng dạng bài toán cụ thể.

Công thức tính góc dựa vào tỷ số lượng giác

Phương pháp tính góc dựa vào tỷ số lượng giác là cách phổ biến và trực tiếp nhất. Với các tỷ số sin, cos, tan, ta có thể tính được góc thông qua hàm arcsin, arccos, arctan.

Khi biết độ dài các cạnh kề và đối của góc cần tính, ta có thể áp dụng công thức: α = arcsin(a/c) hoặc α = arccos(b/c) hoặc α = arctan(a/b), trong đó a là cạnh đối, b là cạnh kề và c là cạnh huyền.

Công thức tính góc dựa vào định lý Pythagore

Định lý Pythagore không chỉ giúp tính cạnh mà còn là công cụ hữu hiệu để tính góc trong tam giác vuông. Khi áp dụng định lý này kết hợp với tỷ số lượng giác, ta có thể tính được các công thức tính góc tam giác vuông một cách chính xác.

Từ công thức a² + b² = c², ta có thể suy ra cos α = b/c = √(1 – a²/c²). Điều này cho phép tính góc α thông qua hàm arccos khi biết độ dài các cạnh liên quan.

Công thức tính góc dựa vào tính chất đường cao

Tính đường cao trong tam giác vuông cung cấp một phương pháp độc đáo để tính góc. Đường cao h từ đỉnh góc vuông đến cạnh huyền tạo ra hai tam giác vuông đồng dạng với tam giác ban đầu.

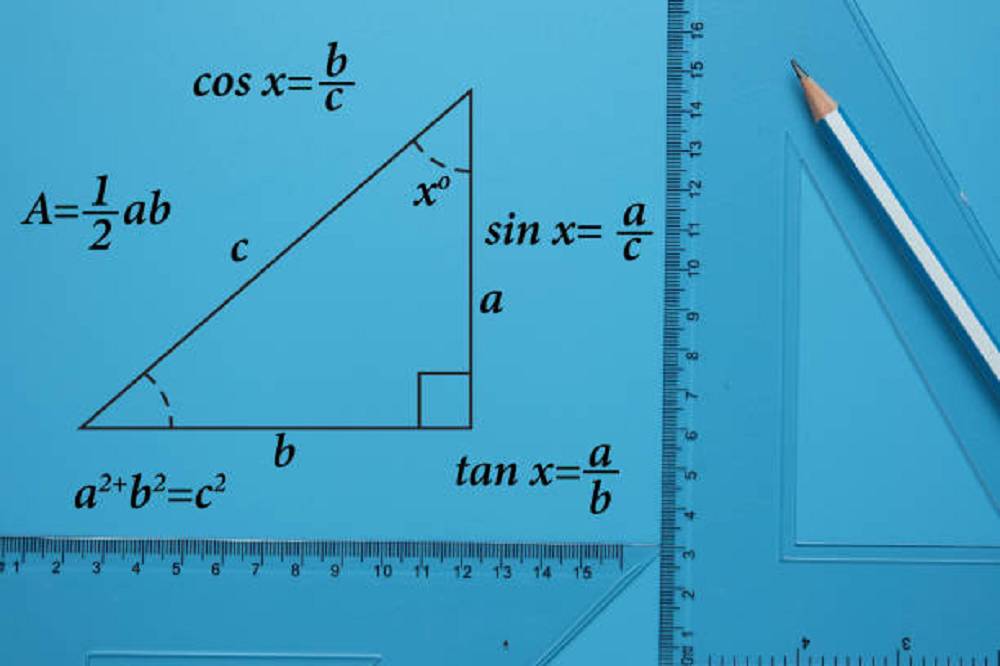
Từ tính chất này, ta có công thức h = a.b/c, từ đó có thể suy ra các góc thông qua tỷ số h/a hoặc h/b. Phương pháp này đặc biệt hữu ích khi cần tính góc trong trường hợp biết đường cao và một cạnh góc vuông.

Phương pháp giải các bài toán về góc trong tam giác vuông

Để giải các bài toán về góc trong tam giác vuông, cần nắm vững các tính chất cơ bản của tam giác vuông. Một tam giác vuông luôn có một góc 90 độ và tổng ba góc bằng 180 độ. Điều này giúp việc tính toán các góc còn lại trở nên đơn giản hơn.

Cách tính góc trong tam giác vuông dựa trên các tỷ số lượng giác và mối quan hệ giữa các cạnh. Khi biết độ dài các cạnh, có thể sử dụng hàm arcsin, arccos hoặc arctang để tính các góc. Ngoài ra, cách chứng minh vuông góc cũng là một công cụ quan trọng để kiểm tra tính chính xác của kết quả.

Các bước giải bài toán tính góc tam giác vuông

Bước đầu tiên là xác định các yếu tố đã biết trong tam giác vuông, có thể là độ dài các cạnh hoặc một góc nhọn. Sau đó, vẽ hình tam giác vuông và ghi rõ các số liệu đã cho.

Tiếp theo, áp dụng phương pháp tính góc tam giác vuông phù hợp dựa trên dữ kiện đã có. Nếu biết hai cạnh, sử dụng tỷ số lượng giác tương ứng. Nếu biết một góc nhọn, tận dụng tính chất tổng các góc trong tam giác.

Cuối cùng, kiểm tra lại kết quả bằng cách thay số vào các công thức hoặc sử dụng máy tính để đảm bảo độ chính xác. Việc kiểm tra giúp tránh các sai sót trong quá trình tính toán.

Ví dụ minh họa và hướng dẫn giải chi tiết

Xét bài toán: Cho tam giác vuông ABC có cạnh huyền c = 10cm, cạnh góc vuông a = 6cm. Tính các góc trong tam giác.

Bước 1: Vẽ hình tam giác vuông ABC, trong đó góc C = 90°
Bước 2: Áp dụng công thức sin A = a/c = 6/10 = 0,6
Bước 3: Tra bảng lượng giác hoặc dùng máy tính: A = arcsin(0,6) = 36,87°
Bước 4: Do B + A = 90°, suy ra B = 53,13°

Kết quả cuối cùng: A = 36,87°, B = 53,13°, C = 90°. Kiểm tra tổng ba góc bằng 180° để đảm bảo tính chính xác của phép giải.

Ứng dụng của tam giác vuông trong thực tế và toán học

Tam giác vuông có nhiều ứng dụng quan trọng trong cuộc sống và toán học. Ứng dụng tam giác vuông trong toán học không chỉ giới hạn ở việc giải các bài toán tam giác vuông cơ bản mà còn mở rộng sang nhiều lĩnh vực phức tạp hơn. Các tính chất đặc biệt của tam giác vuông giúp giải quyết nhiều bài toán thực tiễn một cách hiệu quả.

Ứng dụng trong đo đạc và xây dựng

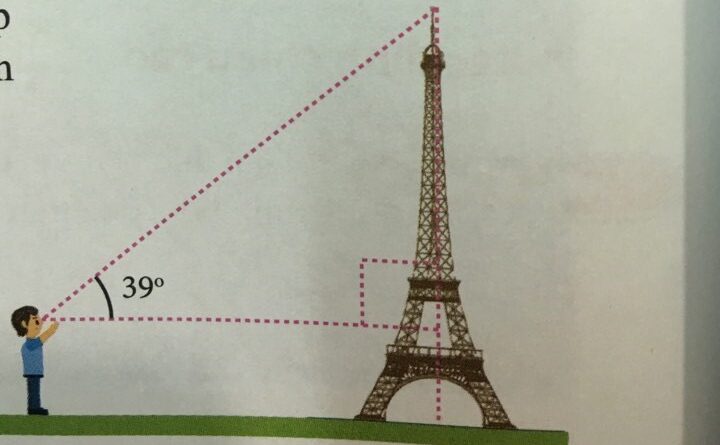
Trong lĩnh vực đo đạc, tam giác vuông đóng vai trò then chốt khi xác định độ cao của các công trình. Các kỹ sư thường sử dụng nguyên lý tam giác vuông kết hợp với máy kinh vĩ để đo độ cao tòa nhà, cột điện hay các công trình cao tầng.

Trong xây dựng, việc đảm bảo các góc vuông chính xác là yếu tố quyết định đến độ thẳng đứng của tường và độ vuông góc của các phòng. Thợ xây thường áp dụng quy tắc 3-4-5 của tam giác vuông để kiểm tra và tạo góc vuông chuẩn xác.

Ứng dụng trong hình học không gian

Tam giác vuông là công cụ quan trọng để giải quyết các bài toán trong không gian ba chiều. Khi tính hình chiếu của điểm lên mặt phẳng, tam giác vuông giúp xác định khoảng cách ngắn nhất từ điểm đến mặt phẳng một cách chính xác.

Trong các bài toán về đa diện, tam giác vuông giúp tính góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng. Đặc biệt, khi nghiên cứu về hình chóp, lăng trụ hay các khối đa diện phức tạp, việc phân tích các tam giác vuông con giúp đơn giản hóa quá trình giải toán đáng kể.

Các tính chất đặc biệt của góc trong tam giác vuông

Góc trong tam giác vuông có những tính chất đặc biệt giúp việc tính toán và giải các bài toán trở nên dễ dàng hơn. Các góc trong tam giác vuông luôn tuân theo những quy luật nhất định về số đo và mối quan hệ với các cạnh.

Việc nắm vững các tính chất này giúp tính toán góc tam giác vuông chính xác và nhanh chóng. Đặc biệt khi áp dụng vào các bài toán thực tế như đo đạc, xây dựng hay thiết kế.

Tổng các góc trong tam giác vuông

Trong tam giác vuông, một góc luôn là 90° (góc vuông), hai góc còn lại là các góc nhọn vuông tù bẹt bao nhiêu độ. Tổng số đo ba góc trong tam giác vuông bằng 180°, do đó tổng hai góc nhọn còn lại bằng 90°.

Theo định lý về góc, hai góc nhọn trong tam giác vuông là hai góc phụ nhau. Điều này có nghĩa nếu biết được một góc nhọn, có thể dễ dàng tìm được góc nhọn còn lại bằng cách lấy 90° trừ đi góc đã biết.

Mối quan hệ giữa các góc và cạnh

Trong tam giác vuông, các góc và cạnh có mối liên hệ chặt chẽ với nhau thông qua các tính chất góc ngoài của tam giác. Cạnh huyền luôn là cạnh dài nhất và nằm đối diện với góc vuông.

Góc nhọn càng lớn thì cạnh đối diện càng dài. Ngược lại, góc nhọn càng nhỏ thì cạnh đối diện càng ngắn. Đây là quy luật quan trọng giúp xác định mối tương quan giữa góc và cạnh trong tam giác vuông.

Các tỷ số lượng giác của góc nhọn trong tam giác vuông (sin, cos, tan) cũng phụ thuộc vào độ dài các cạnh kề và đối diện với góc đó. Điều này tạo nên công cụ hữu hiệu để giải các bài toán liên quan đến tam giác vuông.

Trong việc tính góc tam giác vuông, bạn sẽ khám phá nhiều phương pháp và công thức hữu ích. Bài viết đã trình bày chi tiết các công thức tính góc trong tam giác vuông, cách giải bài toán và ứng dụng thực tế của tam giác vuông. Những kiến thức này không chỉ giúp bạn hoàn thành bài tập mà còn nâng cao khả năng tư duy toán học của mình.