Tính ma trận nghịch đảo và cách tìm ma trận nghịch đảo hiệu quả trong toán học

Tính ma trận nghịch đảo là một trong những khái niệm quan trọng trong đại số tuyến tính. Bài viết này cung cấp kiến thức tổng quan, công thức và phương pháp cụ thể để tìm ma trận nghịch đảo. Nắm vững cách thực hiện sẽ giúp bạn giải quyết hiệu quả các bài toán phức tạp trong toán học.

Tính ma trận nghịch đảo và các phương pháp cơ bản

Trong toán đại số, ma trận nghịch đảo là gì được định nghĩa là ma trận khi nhân với ma trận ban đầu sẽ cho ra ma trận đơn vị. Ma trận nghịch đảo thường được ký hiệu là A^(-1), với A là ma trận ban đầu. Điều kiện để một ma trận có nghịch đảo là ma trận đó phải là ma trận vuông và có định thức khác 0.

Để tính ma trận nghịch đảo, có nhiều phương pháp khác nhau được áp dụng tùy thuộc vào kích thước và đặc điểm của ma trận. Phương pháp phổ biến nhất là sử dụng ma trận phụ hợp và định thức. Theo đó, nghịch đảo của ma trận A được tính bằng công thức: A^(-1) = (1/det(A)) * adj(A), trong đó det(A) là định thức của ma trận A và adj(A) là ma trận phụ hợp của A.

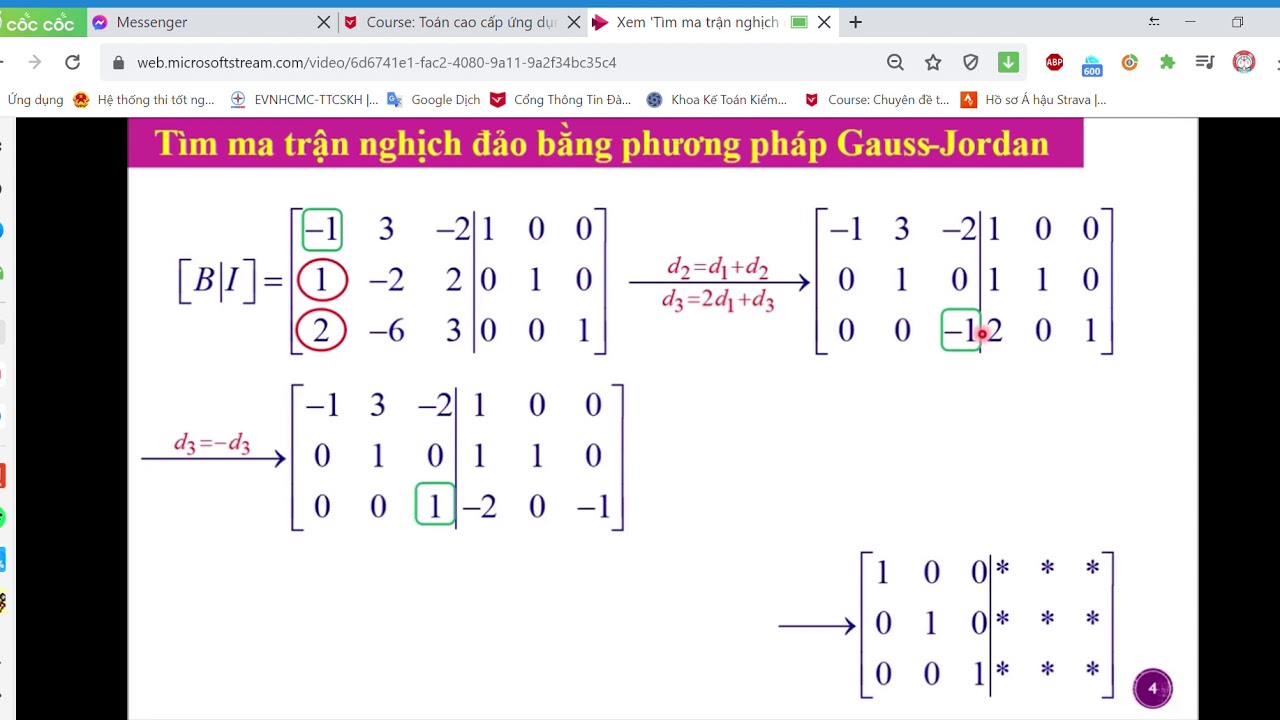
Một phương pháp khác để tìm ma trận nghịch đảo là phương pháp khử Gauss-Jordan. Phương pháp này thực hiện biến đổi sơ cấp trên ma trận mở rộng [A|I] để đưa về dạng [I|A^(-1)]. Phương pháp này đặc biệt hiệu quả với các ma trận có kích thước lớn và được ứng dụng rộng rãi trong các phần mềm tính toán ma trận.

Việc tính toán ma trận nghịch đảo đóng vai trò quan trọng trong nhiều ứng dụng thực tế như xử lý ảnh, điều khiển tự động, và giải các hệ phương trình tuyến tính. Ví dụ trong xử lý ảnh, ma trận nghịch đảo được sử dụng để khôi phục ảnh bị nhiễu hoặc mờ thông qua phép biến đổi ngược.

Khái niệm và tính chất của ma trận nghịch đảo trong toán học

Ma trận nghịch đảo trong toán học là một khái niệm quan trọng trong đại số tuyến tính, đóng vai trò then chốt trong việc giải các hệ phương trình và nhiều ứng dụng thực tiễn. Tương tự như phép chia trong số học, ma trận nghịch đảo cho phép thực hiện phép “chia” trong không gian ma trận.

Định nghĩa ma trận nghịch đảo và ma trận mũ trừ 1

Ma trận mũ trừ 1 là ma trận B thỏa mãn điều kiện AB = BA = I, trong đó A là ma trận ban đầu và I là ma trận đơn vị cùng cấp. Khi nhân ma trận A với nghịch đảo của nó, kết quả luôn cho ma trận đơn vị. Điều này tương tự như trong số học, khi ta nhân một số với nghịch đảo của nó sẽ được 1.

Trong nhiều trường hợp, việc tìm ma trận nghịch đảo giúp giải quyết các bài toán phức tạp một cách hiệu quả, tương tự như cách hàm số đồng biến nghịch biến hỗ trợ việc khảo sát hàm số.

Các điều kiện để một ma trận có nghịch đảo

Ma trận vuông cấp n chỉ có nghịch đảo khi và chỉ khi nó là ma trận khả nghịch. Điều kiện cần và đủ để một ma trận có nghịch đảo bao gồm:

• Định thức của ma trận phải khác 0
• Ma trận phải là ma trận vuông
• Hạng của ma trận phải bằng số chiều của ma trận

Việc kiểm tra các điều kiện trên giúp xác định nhanh chóng khả năng tồn tại nghịch đảo của một ma trận, tránh mất thời gian tính toán không cần thiết.

Tính chất cơ bản của ma trận nghịch đảo

Ma trận nghịch đảo có những tính chất đặc biệt quan trọng trong phép tính ma trận. Nghịch đảo của tích hai ma trận bằng tích nghịch đảo của từng ma trận theo thứ tự ngược lại. Điều này được biểu diễn qua công thức: (AB)^(-1) = B^(-1)A^(-1).

Ngoài ra, nghịch đảo của ma trận chuyển vị bằng chuyển vị của ma trận nghịch đảo. Tính chất này thường được áp dụng trong việc tối ưu hóa các phép tính ma trận phức tạp, đặc biệt trong các ứng dụng xử lý tín hiệu số và học máy.

Việc nắm vững các tính chất này giúp đơn giản hóa nhiều bài toán phức tạp trong đại số tuyến tính và ứng dụng thực tiễn.

Các phương pháp tính ma trận nghịch đảo

Để tính ma trận nghịch đảo, có nhiều phương pháp khác nhau mà chúng ta có thể áp dụng. Công thức tính ma trận nghịch đảo sẽ được triển khai qua 3 phương pháp chính, mỗi phương pháp đều có những ưu điểm và hạn chế riêng. Việc lựa chọn phương pháp phù hợp sẽ giúp quá trình tính toán trở nên hiệu quả hơn. Hướng dẫn tính ma trận nghịch đảo chi tiết sẽ được trình bày trong từng phương pháp cụ thể.

Phương pháp dùng định thức và ma trận phụ hợp

Phương pháp này dựa trên việc tính định thức của ma trận gốc và xây dựng ma trận phụ hợp. Với ma trận vuông A cấp n, ma trận nghịch đảo A^(-1) được tính bằng tích của nghịch đảo định thức và ma trận chuyển vị của ma trận phụ hợp.

Đối với ma trận cấp cao như tính định thức ma trận cấp 4, việc áp dụng phương pháp này đòi hỏi nhiều bước tính toán phức tạp. Tuy nhiên, phương pháp này lại rất hiệu quả với ma trận cấp 2 và cấp 3.

Ưu điểm của phương pháp này là tính chính xác cao và có thể kiểm chứng kết quả dễ dàng thông qua phép nhân ma trận nghịch đảo với ma trận ban đầu.

Phương pháp biến đổi sơ cấp với ma trận đơn vị

Phương pháp này thực hiện song song các phép biến đổi sơ cấp trên ma trận ban đầu A và ma trận đơn vị E cùng cấp. Mục tiêu là biến đổi ma trận A thành ma trận đơn vị, khi đó ma trận E sẽ trở thành ma trận nghịch đảo cần tìm.

Quá trình biến đổi tuân theo 3 nguyên tắc cơ bản:

• Đổi chỗ hai hàng hoặc hai cột
• Nhân một hàng hoặc một cột với một số khác 0
• Cộng vào một hàng (cột) một số lần hàng (cột) khác

Phương pháp này đặc biệt phù hợp khi thực hiện tính toán trên máy tính do các phép biến đổi có tính hệ thống và dễ lập trình.

Phương pháp sử dụng công thức Cramer

Phương pháp Cramer áp dụng cho việc tìm ma trận nghịch đảo thông qua việc giải n hệ phương trình tuyến tính, với n là cấp của ma trận. Mỗi cột của ma trận nghịch đảo được xác định bằng cách giải một hệ phương trình riêng biệt.

Phương pháp này có ưu điểm là dễ hiểu về mặt lý thuyết và phù hợp với việc giảng dạy. Tuy nhiên, với ma trận cấp cao, số lượng phép tính sẽ tăng lên đáng kể.

Trong thực tế, phương pháp này thường được kết hợp với các thuật toán tối ưu để tăng hiệu quả tính toán, đặc biệt khi xử lý các bài toán về xử lý ảnh hay học máy.

Hướng dẫn chi tiết cách tìm ma trận nghịch đảo qua ví dụ

Cách tìm ma trận nghịch đảo được thực hiện thông qua các bước cơ bản: tính định thức, tìm ma trận phụ hợp, tính ma trận liên hợp và cuối cùng là tính ma trận nghịch đảo. Quá trình này đòi hỏi sự tỉ mỉ và chính xác trong từng bước tính toán.

Trước khi đi vào các ví dụ cụ thể, cần lưu ý rằng ma trận nghịch đảo chỉ tồn tại khi định thức của ma trận khác 0. Việc nắm vững các phương pháp tính bảng biến thiên hàm số bậc 2 sẽ giúp quá trình giải các bài tập ma trận nghịch đảo trở nên dễ dàng hơn.

Ví dụ tính ma trận nghịch đảo cấp 2

Ma trận cấp 2 có dạng A = [a11 a12; a21 a22]. Để tìm ma trận nghịch đảo, ta thực hiện các phép tính sau:

• Tính định thức: det(A) = a11.a22 – a12.a21
• Tìm ma trận phụ hợp: adj(A) = [a22 -a12; -a21 a11]
• Tính ma trận nghịch đảo: A^(-1) = (1/det(A)).adj(A)

Áp dụng cho ma trận A = [2 1; 3 4]:
det(A) = 2.4 – 1.3 = 5
adj(A) = [4 -1; -3 2]
A^(-1) = 1/5 = [4/5 -1/5; -3/5 2/5]

Ví dụ tính ma trận nghịch đảo cấp 3

Với ma trận cấp 3, quá trình tính toán phức tạp hơn do có nhiều phần tử hơn. Lấy ví dụ ma trận A = [1 2 0; 3 1 2; 0 2 1]:

Bước 1: Tính định thức bằng quy tắc Sarrus
det(A) = 1.1.1 + 2.2.0 + 0.3.2 – 0.1.2 – 2.3.1 – 1.2.2 = -9

Bước 2: Tìm ma trận phụ hợp bằng cách tính các phần tử liên hợp
adj(A) = [-3 4 -2; 6 1 -2; -6 -1 -3]

Bước 3: Tính ma trận nghịch đảo
A^(-1) = -1/9

Các bài tập mẫu và lời giải

Bài tập 1: Tìm ma trận nghịch đảo của A = [1 2; -1 3]
Lời giải:
det(A) = 1.3 – 2.(-1) = 5
adj(A) = [3 -2; 1 1]
A^(-1) = 1/5

Bài tập 2: Kiểm tra tính khả nghịch của ma trận B = [2 4; 1 2]
Lời giải:
det(B) = 2.2 – 4.1 = 0
Do det(B) = 0 nên ma trận B không khả nghịch.

Các ví dụ trên minh họa rõ các bước cần thiết để tìm ma trận nghịch đảo, từ đơn giản đến phức tạp.

Ứng dụng của ma trận nghịch đảo trong thực tế

Ứng dụng ma trận nghịch đảo đóng vai trò quan trọng trong nhiều lĩnh vực từ khoa học kỹ thuật đến kinh tế xã hội. Việc tính ma trận nghịch đảo giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả như Hocthenao.vn đã phân tích chi tiết. Ma trận nghịch đảo được ứng dụng rộng rãi trong ba lĩnh vực chính: giải hệ phương trình tuyến tính, mã hóa – bảo mật thông tin và xử lý ảnh số.

Giải hệ phương trình tuyến tính

Ma trận nghịch đảo là công cụ mạnh mẽ để giải các hệ phương trình tuyến tính phức tạp. Thay vì sử dụng các phương pháp thủ công như phương pháp Gauss hay phương pháp thế, việc sử dụng ma trận nghịch đảo giúp tìm nghiệm nhanh chóng và chính xác hơn.

Trong thực tế, các kỹ sư xây dựng thường xuyên áp dụng ma trận nghịch đảo để tính toán lực tác động và độ bền của các kết cấu. Ví dụ như công ty ARUP đã sử dụng phương pháp này trong thiết kế tòa nhà 30 St Mary Axe tại London, giúp tối ưu hóa cấu trúc và đảm bảo độ an toàn.

Ứng dụng trong mã hóa và bảo mật

Trong lĩnh vực mật mã học, ma trận nghịch đảo là nền tảng của nhiều thuật toán mã hóa. Khi thông tin được biểu diễn dưới dạng ma trận, việc mã hóa và giải mã được thực hiện thông qua các phép nhân ma trận và tìm ma trận nghịch đảo.

RSA – một trong những hệ thống mã hóa phổ biến nhất hiện nay – sử dụng nguyên lý này. Các ngân hàng và tổ chức tài chính áp dụng ma trận nghịch đảo trong hệ thống bảo mật giao dịch trực tuyến, đảm bảo tính riêng tư và an toàn cho người dùng.

Công nghệ blockchain cũng tận dụng tính chất của ma trận nghịch đảo trong quá trình xác thực và mã hóa các giao dịch, tạo nên một hệ thống bảo mật đáng tin cậy.

Ứng dụng trong xử lý ảnh số

Ma trận nghịch đảo đóng vai trò then chốt trong các thuật toán xử lý ảnh số. Mỗi bức ảnh kỹ thuật số được biểu diễn dưới dạng ma trận các điểm ảnh, và nhiều thao tác xử lý ảnh đòi hỏi việc tính toán ma trận nghịch đảo.

Các phần mềm chỉnh sửa ảnh chuyên nghiệp như Adobe Photoshop sử dụng ma trận nghịch đảo trong các phép biến đổi hình học như xoay, co giãn và biến dạng ảnh. Kỹ thuật này cũng được áp dụng trong việc khôi phục ảnh bị mờ hoặc nhiễu.

Trong lĩnh vực y tế, ma trận nghịch đảo được sử dụng để xử lý ảnh chụp cộng hưởng từ (MRI) và chụp cắt lớp vi tính (CT), giúp bác sĩ có được hình ảnh chẩn đoán chất lượng cao và chính xác.

Tính ma trận nghịch đảo là một khái niệm quan trọng trong toán học, đặc biệt là trong giải hệ phương trình tuyến tính. Bài viết đã cung cấp cái nhìn tổng quát về định nghĩa, tính chất và phương pháp tính ma trận nghịch đảo, cùng với ví dụ và ứng dụng thực tiễn. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết nhiều bài toán toán học phức tạp một cách hiệu quả hơn.