Xác suất có điều kiện là một trong những khái niệm quan trọng nhất trong lý thuyết xác suất. Nội dung này luôn được đánh giá là có khối lượng công thức khổng lồ và khó tiếp cận với không ít người. Bài viết dưới đây, chúng tôi sẽ cung cấp cho các bạn thông tin đầy đủ về xác suất điều kiện.
Xác suất có điều kiện là gì?
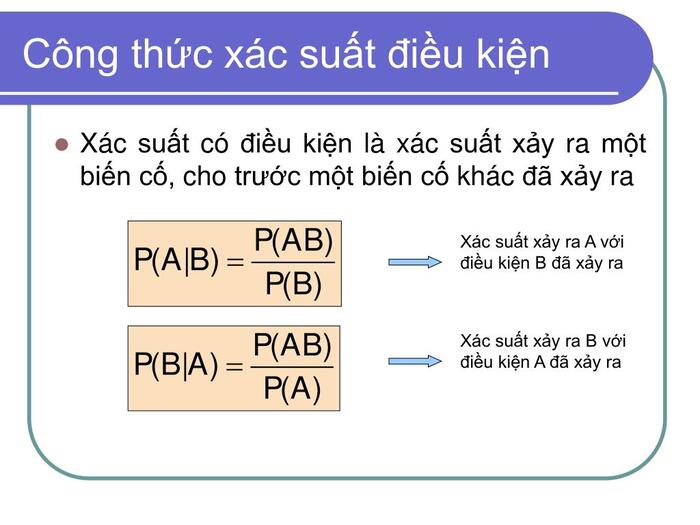
Xác suất có điều kiện là xác suất xảy ra của một sự kiện, với điều kiện một sự kiện khác đã xảy ra. Nó được ký hiệu là P(A|B), đọc là “xác suất của A, biết B đã xảy ra”. Đây là một khái niệm quan trọng trong lý thuyết xác suất. Khái niệm này phản ánh việc thông tin mới có thể thay đổi đánh giá về khả năng xảy ra của một sự kiện.

Xác suất điều kiện giúp chúng ta cập nhật niềm tin hoặc dự đoán dựa trên bằng chứng hoặc thông tin mới nhận được. Nó đóng vai trò quan trọng trong nhiều ứng dụng thực tế, từ y học (như đánh giá khả năng mắc bệnh dựa trên kết quả xét nghiệm).
Công thức xác suất có điều kiện và ví dụ minh họa
Sau khi hiểu conditional probability là gì, chúng ta cùng tìm hiểu rõ hơn về các công thức của nội dung này qua các ví dụ.
Toàn bộ công thức xác suất có điều kiện
Các công thức xs có điều kiện được biểu diễn như sau:

- Công thức cơ bản: P(A|B) = P(A ∩ B) / P(B), với P(B) > 0
- Quy tắc nhân (Multiplication Rule): P(A ∩ B) = P(A|B) * P(B) = P(B|A) * P(A)
- Quy tắc chuỗi (Chain Rule): P(A ∩ B ∩ C) = P(A|B ∩ C) * P(B|C) * P(C)
- Công thức Bayes: P(A|B) = [P(B|A) * P(A)] / P(B)
- Công thức xác suất toàn phần: P(A) = Σ P(A|Bi) * P(Bi), với {Bi} là một phân hoạch của không gian mẫu
- Độc lập có điều kiện: P(A|B ∩ C) = P(A|C), nếu A và B độc lập có điều kiện trên C
- Quy tắc nhân cho các sự kiện độc lập: Nếu A và B độc lập, thì P(A ∩ B) = P(A) * P(B)
Giải đáp các thắc mắc ký hiệu như: P(A) là gi? P(A/B) là gì?…
- P(A): Xác suất của sự kiện A xảy ra.
- P(B): Xác suất của sự kiện B xảy ra.
- P(A|B): Xác suất điều kiện của A khi biết B đã xảy ra. Đọc là “xác suất của A biết B”.
- P(A ∩ B): Xác suất đồng thời của A và B xảy ra. Ký hiệu “∩” đọc là “giao”.
- Σ (sigma): Ký hiệu tổng, dùng trong công thức xác suất toàn phần để tổng hợp các xác suất.
- {Bi}: Tập hợp các sự kiện Bi, thường dùng để chỉ một phân hoạch của không gian mẫu.
- “|”: Trong P(A|B), dấu gạch đứng này đọc là “biết” hoặc “với điều kiện”.
Ví dụ minh họa
Dưới đây là một vài bài tập xác suất điều kiện ví dụ cụ thể để bạn nắm rõ hơn về nội dung này.
Bài tập: Trong một lớp học có 50 học sinh. Trong đó:
- 30 học sinh thích môn Toán
- 25 học sinh thích môn Văn
- 15 học sinh thích cả Toán và Văn
Tính xác suất một học sinh ngẫu nhiên thích môn Toán, biết rằng học sinh đó thích môn Văn.
Lời giải:
- Xác định các sự kiện: A: Học sinh thích môn Toán, B: Học sinh thích môn Văn
- Tính các xác suất cần thiết: P(B) = 25/50 = 1/2 (xác suất thích môn Văn) P(A ∩ B) = 15/50 = 3/10 (xác suất thích cả Toán và Văn)
- Áp dụng công thức xác suất điều kiện: P(A|B) = P(A ∩ B) / P(B)
- Thay số: P(A|B) = (3/10) / (1/2) = 3/5 = 0.6
- Kết luận: Xác suất một học sinh thích môn Toán, biết rằng học sinh đó thích môn Văn, là 0.6 hay 60%.
Giải thích: Trong số những học sinh thích môn Văn, 60% cũng thích môn Toán. Điều này cho thấy có một sự tương quan khá mạnh giữa việc thích môn Văn và thích môn Toán trong lớp học này.
Phân biệt xác suất có điều kiện và xác suất thông thường
Dưới đây là bảng so sánh giữa xác suất thường và xs có điều kiện
| Đặc điểm | Xác suất thường | Xác suất có điều kiện |
| Định nghĩa | Khả năng xảy ra của sự kiện trong toàn bộ không gian mẫu | Khả năng xảy ra của sự kiện, biết một sự kiện khác đã xảy ra |
| Ký hiệu | P(A) | P(A|B) |
| Phụ thuộc | Không phụ thuộc thông tin bổ sung | Phụ thuộc vào sự kiện đã biết |
| Không gian mẫu | Toàn bộ không gian mẫu | Thu hẹp dựa trên điều kiện đã biết |
| Tính toán | Dựa trên tất cả kết quả có thể | Dựa trên kết quả thỏa mãn điều kiện |
| Công thức | P(A) = số trường hợp thuận lợi / tổng số trường hợp | P(A|B) = P(A ∩ B) / P(B) |
| Ứng dụng | Đánh giá khả năng xảy ra ban đầu | Cập nhật đánh giá khi có thông tin mới |
| Ví dụ | Xác suất rút quân bài cơ từ bộ 52 lá | Xác suất rút quân bài cơ, biết là quân đỏ |
Một vài lưu ý về xác suất có điều kiện
Để làm tốt các bài tập xác suất có điều kiện, sau đây là một vài lưu ý bạn không nên bỏ qua.
- Không tương đương: P(A|B) thường không bằng P(B|A). Ví dụ, xác suất một người bị ung thư khi có kết quả xét nghiệm dương tính khác với xác suất một người có kết quả xét nghiệm dương tính khi bị ung thư.
- Phạm vi giá trị: Xác suất điều kiện, giống như xác suất thường, luôn nằm trong khoảng từ 0 đến 1.
- Điều kiện phải xảy ra: P(A|B) chỉ có ý nghĩa khi P(B) > 0. Không thể tính xs có điều kiện nếu sự kiện điều kiện có xác suất bằng 0.
- Ảnh hưởng của thông tin: Thông tin mới có thể làm tăng, giảm hoặc không ảnh hưởng đến xác suất ban đầu.
- Quy tắc chuỗi: Khi có nhiều điều kiện, ta có thể áp dụng quy tắc chuỗi để tính xác suất phức tạp hơn.
Hiểu và áp dụng đúng các lưu ý này sẽ giúp tránh các sai lầm phổ biến khi làm việc với nội dung này.
Lời kết
Nhìn chung, bài viết trên chúng tôi đã cung cấp đầy đủ các thông tin về định nghĩa, các công thức của xác suất có điều kiện. Chúng tôi hy vọng rằng, những kiến thức chúng tôi cung cấp có thể giúp ích cho bạn trong quá trình học tập, nghiên cứu môn học này.