Hướng dẫn chi tiết cách xét dấu hàm bậc 3 và ứng dụng trong bài toán

Xét dấu hàm bậc 3 là kỹ năng cần thiết giúp xác định dấu của biểu thức đa thức bậc 3 qua phân tích nghiệm và đồ thị. Nắm vững các quy tắc và tính chất cơ bản sẽ hỗ trợ bạn giải quyết nhiều bài toán liên quan. Hãy cùng khám phá quy trình và ứng dụng của phương pháp này trong giải toán!

Xét dấu hàm bậc 3 là phương pháp xác định dấu của biểu thức đa thức bậc 3 thông qua việc phân tích nghiệm và đồ thị

Việc xét dấu hàm bậc 3 đóng vai trò quan trọng trong việc phân tích và giải quyết các bài toán liên quan đến đa thức bậc 3. Phương pháp này giúp ta xác định được dấu của biểu thức tại từng khoảng xác định, từ đó có thể vẽ được đồ thị hàm bậc 3 một cách chính xác.

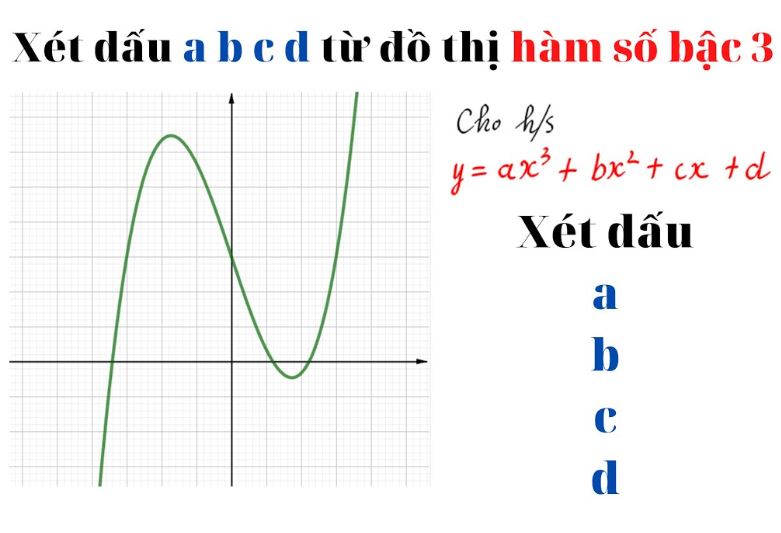
Để thực hiện xét dấu một cách hiệu quả, việc Học toán có phương pháp là rất cần thiết. Trước tiên cần tìm các điểm làm cho hàm số bằng 0, sau đó chia trục số thành các khoảng bởi các điểm này. Việc xét dấu sẽ được thực hiện trên từng khoảng đã chia.

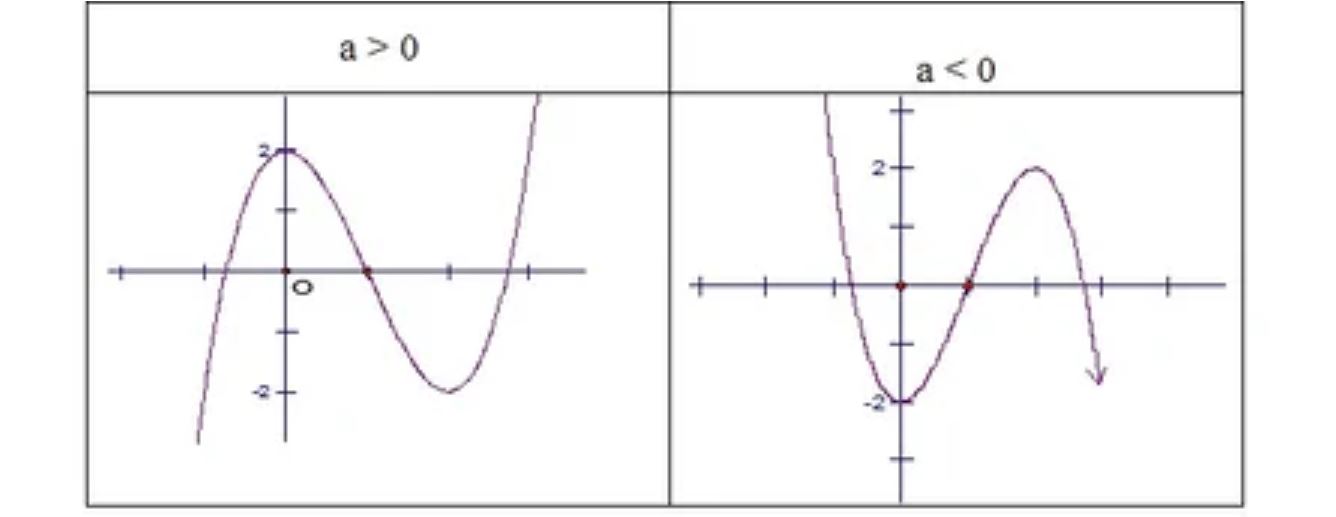
Khi xét dấu, ta cần chú ý đến hệ số của x^3 vì nó quyết định dấu của hàm số khi x tiến đến vô cực. Nếu hệ số dương, đồ thị sẽ đi lên ở vô cực dương và đi xuống ở vô cực âm. Ngược lại, nếu hệ số âm, đồ thị sẽ đi xuống ở vô cực dương và đi lên ở vô cực âm.

Các tính chất cơ bản và đặc điểm của hàm số bậc 3 cần nắm vững trước khi xét dấu

Để phân tích và giải quyết các bài toán liên quan đến tính chất hàm bậc 3, việc nắm vững các đặc điểm cơ bản là vô cùng quan trọng. Các tính chất này không chỉ giúp ta hiểu rõ bản chất của hàm số mà còn là nền tảng để giải quyết các bài toán phức tạp hơn.

Tính liên tục và tính chất đồ thị của hàm bậc 3

Đồ thị của hàm bậc 3 luôn là một đường cong trơn, không có điểm gãy hay điểm gián đoạn. Tính chất này xuất phát từ việc hàm bậc 3 là một hàm đa thức, do đó luôn liên tục trên toàn tập xác định của nó.

Một đặc điểm quan trọng khác là đồ thị hàm bậc 3 luôn có dạng “uốn” đặc trưng, với tối đa hai điểm uốn. Điều này tạo nên hình dạng đặc biệt giúp phân biệt với các dạng hàm số khác.

Mối quan hệ giữa hệ số và nghiệm của phương trình bậc 3

Phương trình bậc 3 có thể có một, hai hoặc ba nghiệm thực, phụ thuộc vào các hệ số của nó. Định lý Viète cho phép ta thiết lập mối liên hệ giữa các nghiệm và hệ số của phương trình.

Khi phân tích nghiệm, cần chú ý rằng tổng các nghiệm bằng âm hệ số của x bậc 2 chia cho hệ số của x bậc 3. Tích các nghiệm bằng âm số hạng tự do chia cho hệ số của x bậc 3.

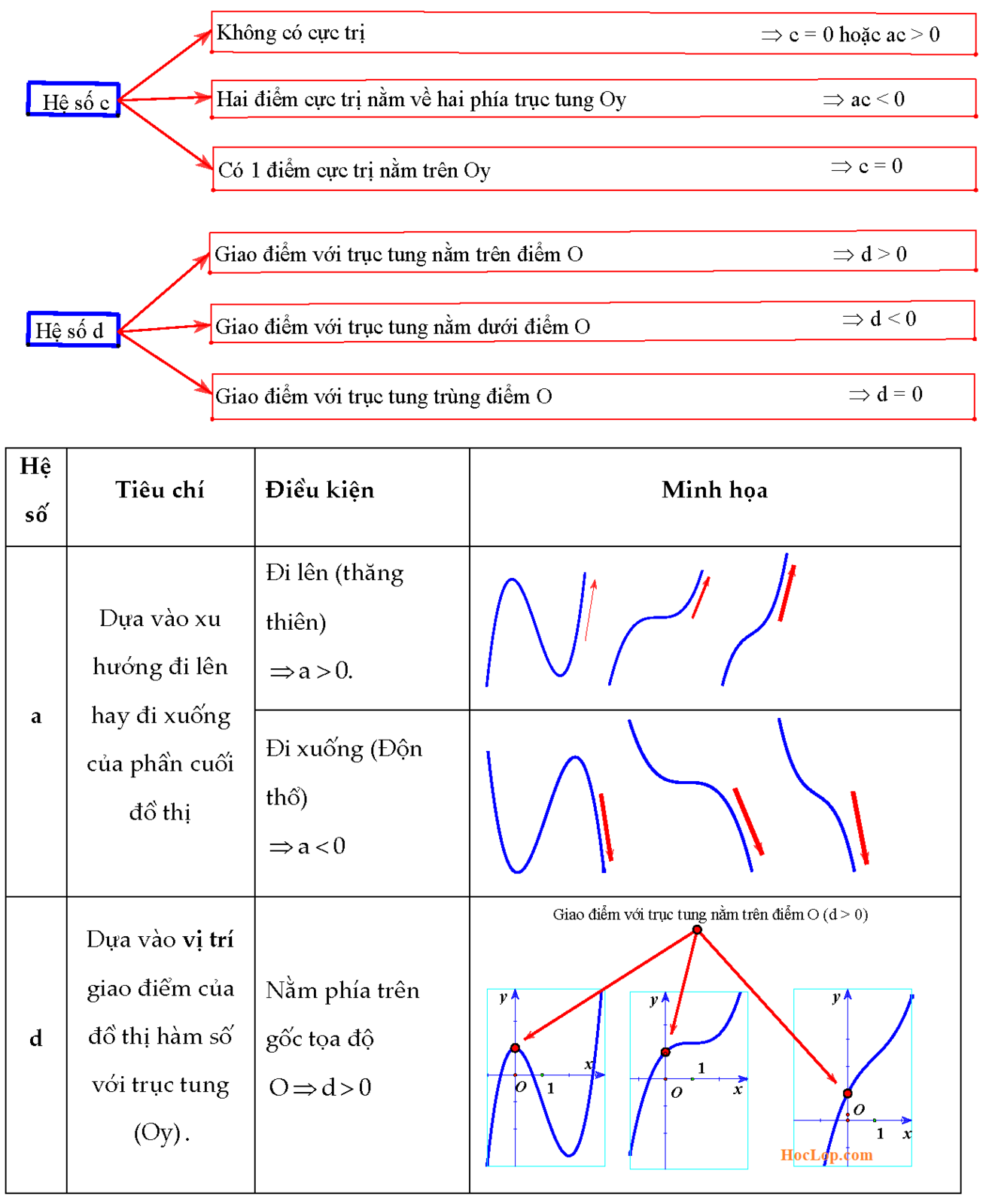
Vai trò của đạo hàm trong việc xác định cực trị

Đạo hàm căn bậc 3 đóng vai trò then chốt trong việc tìm cực trị của hàm số bậc 3. Đạo hàm bậc nhất của hàm bậc 3 là một hàm bậc 2, giúp ta xác định được chính xác vị trí các điểm cực trị.

Thông qua việc giải phương trình đạo hàm bằng 0, ta có thể tìm được tọa độ các điểm cực trị. Điều này rất quan trọng khi cần phân tích sự biến thiên của hàm số hoặc tìm giá trị lớn nhất, nhỏ nhất của hàm trên một khoảng xác định.

Quy trình xét dấu hàm bậc 3 theo số nghiệm của phương trình

Quy tắc xét dấu của hàm bậc 3 phụ thuộc vào số lượng nghiệm thực của phương trình. Việc xác định dấu của hàm số sẽ dựa trên đặc điểm của đồ thị và vị trí các điểm cực trị. Khi phân tích đồ thị, ta cần xem xét các trường hợp khác nhau về số nghiệm để có phương pháp xét dấu phù hợp.

Để xét dấu chính xác, trước tiên cần tìm m để phương trình có 3 nghiệm phân biệt hoặc xác định số nghiệm của phương trình. Sau đó, việc xét dấu sẽ được thực hiện theo từng khoảng xác định dựa trên vị trí các nghiệm.

Trường hợp hàm bậc 3 có một nghiệm thực duy nhất

Khi hàm bậc 3 có một nghiệm thực duy nhất, đồ thị của hàm số sẽ cắt trục hoành tại một điểm duy nhất. Điều này xảy ra khi phương trình không có điểm cực trị hoặc có hai điểm cực trị cùng nằm về một phía so với trục hoành.

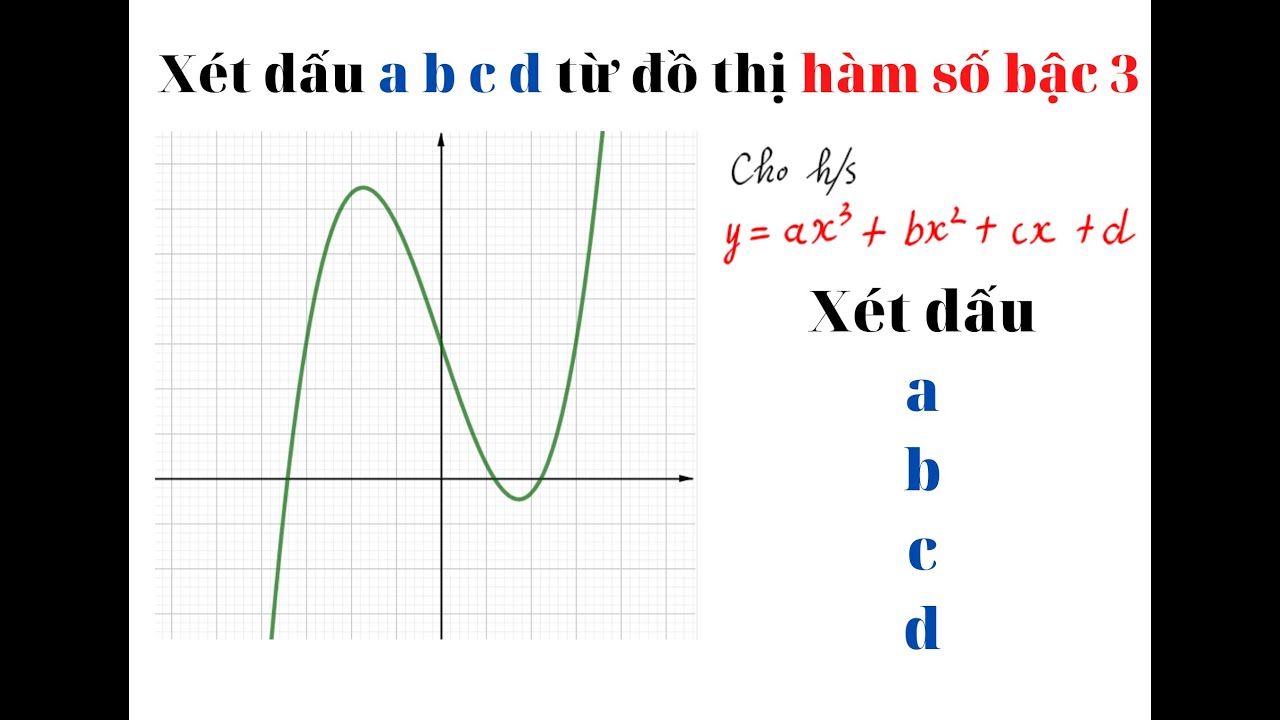
Dấu của hàm số sẽ thay đổi tại nghiệm thực duy nhất này. Nếu hệ số của x³ là dương, hàm số sẽ âm bên trái nghiệm và dương bên phải nghiệm. Ngược lại, nếu hệ số của x³ là âm, hàm số sẽ dương bên trái nghiệm và âm bên phải nghiệm.

Trường hợp hàm bậc 3 có ba nghiệm thực phân biệt

Quy tắc xét dấu của hàm bậc 3 có 3 nghiệm đòi hỏi sự phân tích kỹ lưỡng hơn. Đồ thị hàm số sẽ cắt trục hoành tại ba điểm khác nhau, tạo ra bốn khoảng xét dấu.

Giả sử ba nghiệm thực là x₁ < x₂ < x₃, khi hệ số của x³ dương, dấu của hàm số sẽ thay đổi theo thứ tự: âm trong khoảng (-∞; x₁), dương trong khoảng (x₁; x₂), âm trong khoảng (x₂; x₃), và dương trong khoảng (x₃; +∞). Khi hệ số của x³ âm, dấu sẽ thay đổi theo chiều ngược lại.

Trường hợp hàm bậc 3 có nghiệm kép

Trường hợp hàm bậc 3 có nghiệm kép xảy ra khi đồ thị tiếp xúc với trục hoành tại một điểm. Điểm này vừa là nghiệm của phương trình vừa là điểm cực trị của hàm số.

Nếu hàm có một nghiệm đơn x₁ và một nghiệm kép x₂, dấu của hàm số sẽ thay đổi tại x₁ nhưng không đổi dấu tại x₂. Điều này tạo ra một đặc điểm quan trọng giúp phân biệt với các trường hợp khác khi xét dấu hàm bậc 3.

Phương pháp giải các bài toán xét dấu hàm bậc 3 thường gặp

Việc nắm vững cách xét dấu hàm bậc 3 là kỹ năng quan trọng giúp giải quyết nhiều dạng toán phức tạp. Để xét dấu chính xác, cần phân tích kỹ các yếu tố như hệ số, nghiệm và đạo hàm của hàm số.

Khi áp dụng cách tìm dấu hàm bậc 3, việc phân tích các điểm tới hạn và điểm uốn sẽ giúp xác định chính xác sự thay đổi dấu. Kiến thức về đại số toán là nền tảng quan trọng để thực hiện các bước phân tích này một cách hiệu quả.

Bài toán tìm dấu tại một điểm cụ thể

Để tìm dấu tại một điểm cụ thể, bước đầu tiên là thay giá trị điểm đó vào biểu thức của hàm số. Việc này giúp xác định ngay dấu của hàm tại điểm đang xét.

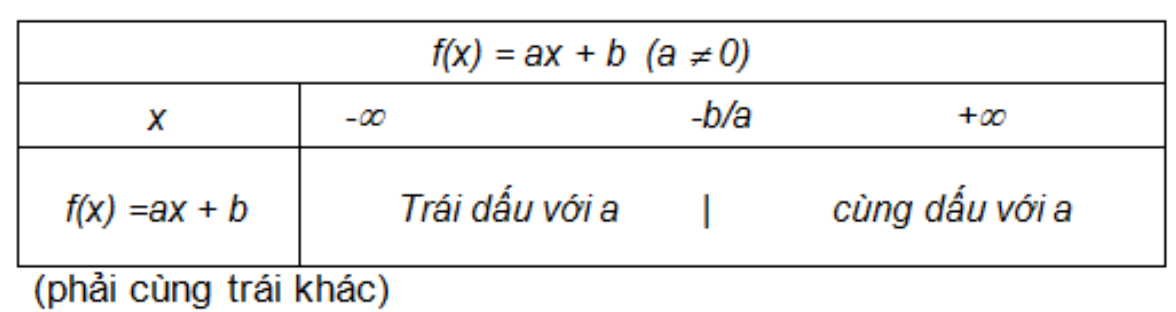
Trong trường hợp điểm cần xét dấu nằm gần nghiệm của hàm số, cần kiểm tra thêm các điểm lân cận để có kết luận chính xác về sự thay đổi dấu. Phương pháp này đặc biệt hữu ích khi giải các bài toán về bất phương trình.

Bài toán xác định khoảng đồng biến và nghịch biến

Để xác định khoảng đồng biến và nghịch biến, ta cần:

• Tìm đạo hàm của hàm số
• Giải phương trình đạo hàm bằng 0
• Lập bảng biến thiên của đạo hàm

Việc phân tích đạo hàm giúp ta thấy được xu hướng tăng giảm của hàm số. Từ đó có thể xác định chính xác các khoảng mà hàm số đồng biến hoặc nghịch biến.

Bài toán tìm tập xác định của biểu thức chứa hàm bậc 3

Khi biểu thức chứa căn thức hoặc mẫu số có hàm bậc 3, việc xác định tập xác định đòi hỏi phải xét kỹ các điều kiện. Thông thường, ta cần giải quyết các bất phương trình có dạng f(x) ≥ 0 hoặc f(x) ≠ 0.

Một số trường hợp đặc biệt có thể xuất hiện khi biểu thức chứa logarit hoặc các hàm lượng giác. Lúc này, việc kết hợp các điều kiện xác định của từng hàm số thành phần sẽ cho ta tập xác định cuối cùng của biểu thức.

Phương pháp giải tối ưu là phân tích riêng từng điều kiện, sau đó kết hợp chúng lại theo quy tắc giao của các tập hợp để có được kết quả chính xác nhất.

Ứng dụng của việc xét dấu hàm bậc 3 trong giải toán

Xét dấu hàm số bậc 3 là một kỹ thuật quan trọng giúp giải quyết nhiều bài toán phức tạp. Việc áp dụng nguyên lý xét dấu cho phép xác định chính xác các khoảng dương, âm của hàm số, từ đó tìm ra lời giải cho nhiều dạng toán khác nhau.

Ứng dụng hàm bậc 3 được thể hiện rõ nét qua 3 nhóm bài toán chính: giải bất phương trình, tìm cực trị và khảo sát biến thiên. Mỗi nhóm bài toán đều đòi hỏi việc nắm vững kỹ thuật xét dấu để đạt kết quả chính xác.

Giải bất phương trình bậc 3

Khi giải bất phương trình bậc 3, việc xét dấu giúp xác định chính xác các khoảng nghiệm. Đầu tiên, cần tìm nghiệm của phương trình bậc 3 tương ứng bằng phương pháp phân tích thừa số hoặc công thức Cardan.

Sau khi có các nghiệm, tiến hành lập bảng xét dấu để xác định dấu của hàm số tại các khoảng giữa các nghiệm. Điều này giúp tìm ra tập nghiệm chính xác của bất phương trình ban đầu.

Tìm giá trị lớn nhất, nhỏ nhất của hàm số

Để tìm cực trị của hàm bậc 3, cần xét dấu đạo hàm cấp một. Các điểm mà đạo hàm bằng 0 hoặc không xác định chính là các điểm có khả năng là cực trị.

Việc xét dấu đạo hàm giúp xác định sự tăng giảm của hàm số tại các khoảng. Từ đó có thể kết luận chính xác giá trị lớn nhất, nhỏ nhất của hàm số trên miền xác định.

Ví dụ thực tế từ GS. Ngô Bảo Châu cho thấy phương pháp này đặc biệt hiệu quả khi giải các bài toán tối ưu trong thực tế, như tối ưu hóa chi phí sản xuất hay thiết kế hình học.

Khảo sát sự biến thiên của hàm số

Khảo sát biến thiên đòi hỏi phải xét dấu cả đạo hàm cấp một và cấp hai. Đạo hàm cấp một cho biết tính đơn điệu, trong khi đạo hàm cấp hai xác định độ cong của đồ thị.

Bằng cách lập bảng biến thiên chi tiết, có thể vẽ được đồ thị chính xác của hàm số. Điều này giúp hình dung rõ ràng về hình dạng và đặc điểm của hàm số.

Kết quả khảo sát còn giúp xác định các điểm uốn, các khoảng lồi lõm và các đặc trưng khác của đồ thị hàm số một cách chính xác và có hệ thống.

Xét dấu hàm bậc 3 là một kỹ năng toán học quan trọng, giúp phân tích biểu thức đa thức bậc 3 một cách chính xác. Qua bài viết, bạn đã nắm vững quy trình xét dấu và các trường hợp đặc biệt của hàm bậc 3. Việc hiểu rõ về cách xét dấu này không chỉ hỗ trợ trong việc giải các bài toán mà còn giúp bạn khảo sát sự biến thiên của hàm số một cách hiệu quả. Sử dụng kiến thức này để nâng cao khả năng giải toán của bạn!