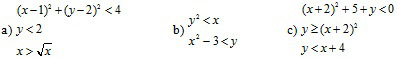TS. Nguyễn Huy Đoan*
Giới thiệu
Trong hội thảo về PPDH do Viện Khoa học GD tổ chức tại Quảng Ninh năm 2011, tôi đã có tham luận “Chương trình và SGK – mong muốn và hiện thực”. Tham luận phản ánh một tình trạng có thực: các tác giả chương trình và SGK Toán đã cố gắng bỏ bớt một số nội dung kiến thức, bỏ bớt một số khái niệm phức tạp, giảm số lượng bài tập đến mức tối đa và không chọn những bài tập khó,… với mục đích “giảm tải”. Thế nhưng dư luận xã hội vẫn cho rằng chương trình và SGK của ta là quá nặng, nhiều kiến thức “thừa”(?). Tham luận đã phân tích một số nguyên nhân và cho rằng các giải pháp giảm tải như trên chỉ là hình thức, không phù hợp và thậm chí là phản tác dụng.
Trong bài viết này, trên cơ sở những nghiên cứu bước đầu, một lần nữa tôi muốn chứng minh rằng nội dung chương trình của ta không những không quá nặng mà còn quá nghèo nàn so với nhiều nước tiên tiến trên thế giới; phương pháp tiếp cận thể hiện trong SGK Toán còn nhiều điều cần trao đổi và học tập. Trong bối cảnh xu hướng hội nhập quốc tế là tất yếu và đang diễn ra ngày càng sâu sắc, điều đó cũng đủ để rút ra một số khuyến nghị dành cho các nhà phát triển chương trình và viết SGK về tính bao quát của nội dung kiến thức đưa vào SGK, về tính liên kết chặt chẽ giữa các nội dung ấy và một số vấn đề khác.
Nội dung
1. Về nội dung chương trình môn Toán Phổ thông Trung học
Trong số rất nhiều vấn đề cần quan tâm về nội dung chương trình, tôi muốn nhấn mạnh rằng SGK Toán của Việt Nam, chỉ nói riêng về khối lượng kiến thức, còn chưa theo kịp nhiều nước trên thế giới. Điều này có vẻ trái ngược với nhiều ý kiến được đăng tải trên các phương tiện truyền thông. Nhưng thực tế SGK Toán của nhiều nước hiện nay đã bao quát một phạm vi kiến thức khá rộng, gồm hầu hết các kiến thức truyền thống (hiểu theo nghĩa các kiến thức đã từng được đưa vào dạy ở các trường Phổ thông Trung học từ những năm trước khi máy tính và công nghệ thông tin phát triển), kết hợp với những kiến thức hiện đại, có nhiều ứng dụng trong thực tiễn đời sống và khoa học kĩ thuật.
Để chứng minh nhận xét này, xin dẫn ra dưới đây những nội dung cụ thể (các chữ in đậm – nghiêng chỉ các thuật ngữ, khái niệm, kiến thức và kĩ năng mà Việt Nam không đưa vào SGK Toán hoặc chỉ đưa vào một cách hạn chế).
1.1. Khi trình bày một số nội dung cơ bản, SGK Toán của Việt Nam đã bỏ qua nhiều khái niệm liên quan, có ý nghĩa thực tiễn và cập nhật.
– Các khái niệm tương ứng (Đức: Zuordnung), tương ứng đa trị, tương ứng đơn trị, tương ứng một – một, hay quan hệ được [1], [2] đưa vào khá sớm, qua rất nhiều ví dụ thực tế, nhằm dẫn đến khái niệm hàm số. [4] cũng định nghĩa hàm số thông qua khái niệm ánh xạ. Chú ý rằng ngay từ khi bắt đầu làm quen, các khái niệm hàm số đã được định nghĩa gắn liền tập xác định và tập giá trị. Đối với hàm số y = f(x), [2] còn gọi x là đầu vào và y là đầu ra và đưa ra khái niệm biến độc lập và biến phụ thuộc. Vấn đề đồ thị của một tương ứng hay một quan hệ, cho dù đồ thị chỉ gồm vài điểm rời rạc cũng rất được chú trọng. Bởi vậy các thuật ngữ đồ thị liên tục, đồ thị rời rạc cũng được nhắc tới.
– Khi nói đến tỉ số, hầu hết SGK Toán các nước đều đề cập đến một khái niệm quan trọng và thường gặp trong thực tiễn, đó là tỉ giá (rate: tỉ số của hai đại lượngkhông cùng đơn vị). Trong [2] có một bài riêng về 3 khái niệm: tỉ số, tỉ giá và tỉ lệ thức. Với sự phân biệt như thế và do tính thực tiễn của các hàm số, [1] và [2] còn gọi Dy/Dx là tỉ giá biến thiên.
1.2. Một số nội dung chỉ được trình bày hạn chế trong SGK Toán của Việt Nam
– Biến đổi đồ thị hàm số. Trong SGK Toán Việt Nam, vấn đề biến đổi đồ thị hàm số chỉ giới hạn ở phép tịnh tiến đồ thị song song với trục toạ độ và cũng được đề cập hết sức đơn giản trong [9] (Đại số 10 Nâng cao). Biến đổi đồ thị hàm số, còn gọi là biến đổi hàm số là vấn đề được SGK các nước đặc biệt quan tâm. [2] dành một chương nói về biến đổi hàm số tuyến tính, trong đó có mô tả Phép tịnh tiến đồ thị song song với các trục toạ độ, phép quay quanh một điểm, phép đối xứng qua một trục toạ độ. Vấn đề này được nhắc lại khi nói về hàm số bậc hai, hàm số giá trị tuyệt đối, hàm đa thức, hàm số hữu tỉ, hàm căn, hàm số mũ, hàm số logarithm, hàm số lượng giác, đồng thời bổ sung thêm phép co dãn (compressing or stretching) đồ thị theo chiều ngang hay chiều dọc. Liên quan đến vấn đề này, [2] đưa ra khái niệm họ hàm số và hàm bố mẹ. Trong [1], các phép biến đổi hàm số cũng được trình bày một cách hệ thống, bắt đầu từ hàm số bậc hai, như một phương pháp chủ yếu trong việc khảo sát các hàm số sơ cấp. Thay cho hàm bố mẹ, [1] đưa vào khái niệm các hàm số chuẩn, đó là các hàm số y = 1, y = x (đường thẳng nguyên thuỷ), y = x2 (parabol chuẩn), y = x3, y = x4, y = 1/x, y = 1/x2, y = |x|, y = sgn(x), y = sin(x) và y = cos(x). [4] cũng nhắc tới các phép tịnh tiến, co–dãn và áp dụng vào đồ thị của hàm số mũ, nhất là hàm số lượng giác.
– Khảo sát hàm số. Các hàm số được khảo sát bằng phương pháp sơ cấp không chỉ có hàm số tuyến tính, hàm số bậc hai, hàm số luỹ thừa y = xn, hàm số mũ y = ax, hàm số logarithm y = logax, các hàm số lượng giác cơ bản, mà còn có hàm số đa thức bậc 3, 4; hàm số hữu tỉ và các hàm số có thể được suy ra các hàm số đơn giản hơn nhờ các phép biến đổi hàm số.
– Bất phương trình hai ẩn và hệ bất phương trình hai ẩn. Nếu như trong [8] và [9], vấn đề này chỉ giới hạn ở bất phương trình bậc nhất hai ẩn thì trong [1] có đề cập đến bất phương trình và hệ bất phương trình hai ẩn tổng quát hơn. Dưới đây là một bài tập trong SGK lớp 9: Xác định tập nghiệm của hệ bất phương trình (không sử dụng kí hiệu “{“):
– Thống kê. Bên cạnh những vấn đề như SGK Toán của VN, [12] còn đề cập đến nhiều khái niệm khác như: các số tứ phân vị (quartiles), thập phân vị (deciles), bách phân vị; các số đo độ phân tán: khoảng biến thiên (rang), khoảng tứ phân vị (inter-quartile range); tần số tích luỹ (cumulative frequency), bảng tấn số tích luỹ, đường cong / đa giác tần số tích luỹ (cumulative frequency curve/polygon).
– Xác suất. Bản thảo đầu tiên của [8] và [9] có đề cập vấn đề xác suất có điều kiện. Song đáng tiếc là đã bị loại bỏ do sức ép của “giảm tải”. Trong khi đó, xác suất có điều kiện đều xuất hiện trong tất cả các SGK nước ngoài mà tôi tham khảo.
– Các phép biến hình trong mặt phẳng. Ngoài các phép biến hình như tịnh tiến, đối xứng tâm, đối xứng trục, quay, vị tự, [2], [3], [12], [13] còn đề cập đến phép trượt (shear) theo một đường thẳng và phép co-dãn theo một phương cùng với các thuật ngữ hệ số trượt và hệ số co-dãn. Hơn nữa, các phép biến hình đều được xét trên mặt phẳng toạ độ.
– Quỹ tích. [3] đã dành 5 bài để trình bày về quỹ tích phẳng. Ngoài một số quỹ tích thông thường, còn có bài quỹ tích liên quan đến diện tích, bài quỹ tích và bất đẳng thức nói về quỹ tích là một phần của mặt phẳng, như hình tròn hay nửa mặt phẳng.
1.3. Một số nội dung không được đề cập trong SGK của Việt Nam
– Trong [2], [6] có giới thiệu khái niệm ma trận, các phép toán cộng trừ hai ma trận cùng cấp, nhân ma trận với một số, nhân hai ma trận định thức và ma trận
nghịch đảo; Áp dụng giải hệ phương trình tuyến tính, dùng ma trận để thực hiện các phép biến đổi hình học (tịnh tiến, vị tự, đối xứng, quay). Đặc biệt trong chương trình của Anh, [12] và [13] còn đề cập đến ma trận của phép biến hình trong mặt phẳng.
– Mô hình hoá (modelling) là quá trình lựa chọn và sử dụng toán học và thống kê một cách thích hợp để phân tích những tình huống thực nghiệm, nhằm hiểu rõ các tình huống ấy để có những quyết định tốt hơn. [13] coi đây là một chủ đề lớn trong chương trình. Trong các sách, vấn đề mô hình hoá thường gắn với thống kê và xác suất đồng thời còn xuất hiện rải rác ở những thời điểm có nội dung phù hợp. Mô hình hoá chính là một nội dung rèn luyện kĩ năng phát hiện và giải quyết vấn đề.
2. Về phương pháp tiếp cận nội dung chương trình
Nhìn chung, phương pháp tiếp cận các nội dung kiến thức toán phổ thông trung học của các nước có những đặc điểm sau:
(1) Đơn giản hoá tối đa con đường truyền thụ kiến thức cho HS, cho dù về bản chất, nội dung kiến thức ấy là rất phức tạp. Quán triệt quan điểm thực tiễn và liên thông.
(2) Các mạch kiến thức lớn đều được trình bày theo một quan điểm hay một tư tưởng nhất quán xuyên suốt các lớp học.
(3) Các khái niệm hay kiến thức khó nhưng quan trọng được dẫn dắt theo con đường “xoáy trôn ốc” hay phương pháp “đồng tâm”, bước trước chuẩn bị cho HS tiếp thu kiến thức ở bước sau.
(4) Chú trọng rèn luyện kĩ năng phát hiện và giải quyết vấn đề, kĩ năng mô hình hoá toán học, kĩ năng giải toán; coi trọng tư duy thuật toán, rèn luyện tư duy trừu tượng, tư duy phê phán.
Trong khuôn khổ của bài viết, xin được làm rõ thêm hai nhận xét 2 và 3 qua một trong các chủ đề kiến thức quan trọng trong chương trình Toán Phổ thông Trung học ở tất cả các nước, đó là hàm số. Tư tưởng chủ đạo của [1] và [2] đối với chủ đề này là:
– Về xây dựng khái niệm, xem hàm số như là một mô hình toán học của các quan hệ giữa các đại lượng trong thực tế.
– Về phương pháp nghiên cứu, lấy biến đổi hàm số là công cụ chủ yếu.
– Về mặt sư phạm, quán triệt phương pháp “xoáy trôn ốc”.
Ở Việt Nam, khái niệm Hàm số được đưa vào ở lớp 7 (rất sơ lược, không gắn với tập xác định và không qua một khái niệm trung gian nào) và lớp 10 (định nghĩa chính xác hơn, có tập xác định nhưng không định nghĩa tập giá trị). Có thể thấy khái niệm quan trọng này đã được tiếp cận một cách vội vàng, phi thực tiễn và né tránh nhiều nội dung bị coi là “khó”.
Trong khi đó, để chuẩn bị định nghĩa hàm số, [1] và [2] đã chuẩn bị rất kĩ; những vấn đề càng khó, càng tinh tế thì càng được nhấn mạnh và nhắc lại nhiều lần, với nhiều hình thức khác nhau và có nội dung gắn với thực tiễn.
Dưới đây là các bảng liệt kê kiến thức, thể hiện con đường tiếp cận nội dung Hàm số trong [1] và [2], qua đó ta có thể thấy rõ các tư tưởng chủ đạo nêu trên.
Bảng 1. Con đường tiếp cận nội dung Hàm số trong [1]
|
Lớp |
Khái niệm, thuật ngữ, kĩ năng |
Hàm số cụ thể |
| Lớp 6 | – Tương ứng: khái niệm; các cách biểu diễn (bảng, đồ thị, biểu đồ, mô tả). | – Tương ứng tỉ lệ thuận và tỉ lệ nghịch: cách nhận biết, đồ thị (rời rạc). |
| Lớp 7 | – Tương ứng: nhắc lại lớp 6.– Tương ứng đơn trị, tương ứng đa trị, tương ứng 1–1. | – Tương ứng tỉ lệ thuận: định nghĩa, đồ thị; 3 định lí (bài toán cơ bản).– Tương ứng tỉ lệ nghịch: định nghĩa, đồ thị; 3 định lí (bài toán cơ bản). |
| Lớp 8 | – Tương ứng: ôn tương ứng 1–1.– Hàm số, đối số, giá trị hàm số, tập xác định, tập giá trị, các cách cho hàm số, cách nhận biết một hàm số. Đồ thị.– Tính tăng, giảm của hàm số tỉ lệ thuận.
– Tham số m và n trong f(x) = mx + n (chuẩn bị cho biến đổi hàm số). – Tính đơn điệu, 0–điểm của hàm số. |
– Tương ứng tỉ lệ, Hàm số tỉ lệ thuận, đồ thị (đường thẳng nguyên thuỷ).– Hàm số tỉ lệ nghịch, đồ thị (hyperbol).– Hàm số tuyến tính: tính chất, độ dốc, cách vẽ đồ thị, đường thẳng qua hai điểm, đường thẳng vuông góc và song song.
– Hàm số giá trị tuyệt đối: đồ thị và tính chất. |
| Lớp 9 | – Phép tịnh tiến lên, xuống. – Phép tịnh tiến sang trái, phải. – Tác động của hệ số a trong y = ax2 (chuẩn bị cho phép co–dãn).
– Hàm số chẵn, hàm số lẻ. – Hyperbol, đường tiệm cận. – Hàm số ngược: tổng quan về hàm số ngược của hàm số luỹ thừa với số mũ tự nhiên, số mũ hữu tỉ dương. – Tác động của hệ số k trong y = kxn. – Ví dụ về giá trị cực đại toàn thể và giá trị cực đại địa phương của hàm số (làm quen). |
– Hàm số bậc hai: định nghĩa, parabol, các dạng phương trình của hàm số bậc hai, parabol chuẩn (normalparabel).Dạng chuẩn tắc (normatform) của hàm số bậc hai f(x) = x2 + px + q;Cách đưa hàm số bậc hai tổng quát về dạng y = a(x + d)2 + e.
– Hàm số luỹ thừa (ví dụ và đồ thị); hàm số luỹ thừa với số mũ n (xét các trường hợp n = 0, 1; n > 0; n < 0). – Hàm số căn bậc hai và tính chất. – Hàm số hữu tỉ nguyên, hữu tỉ phân và tính chất. |
| Lớp 10 | – Tăng trưởng tuyến tính, tăng trưởng mũ. Mô hình tăng trưởng rời rạc.– Hàm số y = ax+d (ôn phép tịnh tiến). – Hàm số tuần hoàn: chu kì, chu kì nhỏ nhất (gắn với chuyển động quay).
– Hàm số f(x) = a.sin(bx + c) (áp dụng các phép biến đổi hàm số). – Ôn tổng thể về hàm số: khái niệm, tính đơn điệu, 0–điểm, tính đối xứng, tính khả nghịch, tác động của các tham số (c.f(x), f(c.x), f(x) + c và f(x + c)). – Mô tả sự biến thiên của hàm số (chuẩn bị cho lớp trên). |
– Hàm số mũ (y = c.ax): hàm số y = ax,hàm số y = ex (dùng trong máy tính).– Phép tính logarithm và hàm số logarithm.
– Hàm số sin, cosin và tang: tập xác định, tập giá trị, tính tuần hoàn, 0–điểm, tính đơn điệu, giá trị lớn nhất và nhỏ nhất, tính đối xứng. |
| Lớp 11 | – Nhắc lại các vấn đề về tương ứng và hàm số. Hàm số thực, các phép biến đổi hàm số, các hàm số chuẩn.– Giới hạn của dãy số và hàm số. | Ôn lại các hàm số đã học. |
Bảng 2. Con đường tiếp cận nội dung Hàm số trong [2] (gồm 2 tập, không viết theo lớp):
|
Chương |
Khái niệm, thuật ngữ, kĩ năng |
Hàm số cụ thể |
| Tập I | ||
|
Chương 1 |
Giới thiệu về hàm số: đầu vào (input), đầu ra (output). | |
|
Chương 4 |
– Đồ thị của sự tương quan.– Đồ thị rời rạc và đồ thị liên tục. – Quan hệ, các cách biểu diễn một quan hệ.
– Hàm số: miền xác đinh, miền giá trị, cách nhận biết, cách viết hàm số, quy tắc hàm, kí pháp hàm, biến độc lập, biến phụ thuộc. Vẽ đồ thị của hàm số. – Biểu đồ từng điểm và đường xu hướng (scatter plots and trend lines). |
– Cấp số cộng: dãy số, số hạng, công sai. |
|
Chương 5 |
– Giao điểm với các trục toạ độ.– Tỉ giá biến thiên, độ dốc của đường thẳng.– Biến đổi hàm số tuyến tính.
– Họ hàm số, hàm số bố mẹ. – Phép tịnh tiến, quay, đối xứng. – Giá trị lớn nhất và giá trị nhỏ nhất của hàm số. |
– Hàm số tuyến tính: cách nhận biết.– Biến thiên thuận: cách nhận biết, các bài toán, đồ thị.– Đường thẳng dạng độ dốc–giao điểm, dạng điểm–độ dốc, qua 2 điểm.
Độ dốc của các đường thẳng song song và vuông góc. – Hàm số giá trị tuyệt đối. |
|
Chương 9 |
– Giá trị lớn nhất, giá trị nhỏ nhất và Zero của hàm số.– Biến đổi hàm số bậc hai: hàm số bậc hai bố mẹ; tịnh tiến lên, xuống. | – Hàm số bậc hai: cách nhận biết, các đặc trưng của hàm số bậc hai.– Parabol: đỉnh, trục đối xứng, cách tìm trục đối xứng và đỉnh, cách vẽ. |
|
Chương 11 |
– Tăng trưởng và suy giảm mũ.– Lãi kép, chu kí bán rã. – Phân biệt các mô hình tuyến tính, bậc hai và mũ.
– Phép tịnh tiến lên, xuống, trái phải. |
– Cấp số nhân, công bội.– Hàm số mũ f(x) = abx: Đồ thị.– Hàm số căn bậc hai: họ hàm số dạng y = . |
|
Chương 12 |
– Hàm số gián đoạn. – Đường tiệm cận: cách tìm.– Phép tịnh tiến hàm số.
– Ôn: hàm số bố mẹ của các họ hàm số: tuyến tính, bậc hai, căn bậc hai, hữu tỉ. |
– Biến thiên nghịch: cách nhận biết, đồ thị, tính chất, bài toán.– Hàm số hữu tỉ: các hàm số dạngy = + c.
– Sử dụng đường tiệm cận trong vẽ đồ thị hàm số. |
|
Tập II |
||
|
Chương 1 |
Ôn: Quan hệ và hàm số, kí pháp hàm, các phép biến đổi hàm số, họ hàm số và hàm số bố mẹ. | |
|
Chương 2 |
– Các phép biến đổi hàm số tuyến tính: tịnh tiến, đối xứng, co–dãn và phối hợp các phép biến đổi.– Hồi quy, tương quan, đường thẳng phù hợp nhất (line of best fit). | – Hàm số tuyến tính.– Hàm số giá trị tuyệt đối, họ hàm số y = k |x + a| + b.– Đường cong phù hợp với mô hình tuyến tính. |
|
Chương 5 |
– Dùng các phép biến đổi hàm số (có thêm phép co–dãn) để vẽ đồ thị hàm số bậc hai.– Hồi quy bậc hai (quadratic regression). | – Hàm số bậc hai: tính chất của hàm số bậc hai dạng chuẩn (standard form).– Đường cong phù hợp với mô hình bậc hai. |
|
Chương 6 |
– Hàm số đa thức. Đường cong phù hợp với mô hình đa thức. | |
|
Chương 7 |
– Quan hệ ngược, hàm số ngược.– Hồi quy mũ. – Hồi quy logarithm. | – Hàm số mũ và hàm số logarithm. Đường cong phù hợp với mô hình mũ và mô hình logarithm. |
|
Chương 8 |
– Hàm số hữu tỉ và hàm căn. | |
|
Chương 13 |
– Hàm số lượng giác. |
3. Một số khuyến nghị
(1) Khi xây dựng chương trình, dù theo định hướng nào, cũng cần chú ý đến mặt bằng chung về nội dung kiến thức của các nước tiên tiến; liệu pháp “giảm tải” không phải là ‘cắt bỏ’ mà là ‘thu gọn’ kiến thức, kết hợp với đổi mới phương pháp tiếp cận.
(2) Cần có cái nhìn xuyên suốt cả các cấp học, lớp học theo từng chủ đề kiến thức, thể hiện rõ trong chương trình đâu là những kiến thức trung tâm, cơ bản, và đâu là tư tưởng chủ đạo về mặt phương pháp nghiên cứu của chủ đề kiến thức đó.
(3) Nên chăng, ngay từ khi xây dựng chương trình đã cần đưa ra định hướng và những nội dung hạn chế trong các kì thi tốt nghiệp và cả thi tuyển sinh đại học. SGK cũng cần đưa ra những nội dung luyện thi tốt nghiệp phổ thông và luyện thi đại học (nếu vẫn chủ trương tổ chức thi vào đại học).
(4) SGK không chỉ chú trọng phát triển năng lực phát hiện và giải quyết vấn đề, năng lực làm việc theo nhóm của HS mà còn cần quan tâm đến năng lực tự học, năng lực đọc và diễn đạt các nội dung chuyên ngành – điều mà SGK hiện nay chưa thực sự quan tâm.
(5) Không nên quá hạn chế về số lượng bài tập. Việc cung cấp nhiều bài tập trong SGK với sự phân loại hợp lí sẽ vừa giúp GV lựa chọn được bài phù hợp với đối tượng HS mà GV đang trực tiếp giảng dạy, vừa giúp HS có những bài tập phù hợp để luyện tập khi cần.
TÀI LIỆU THAM KHẢO
1. Mathematik plus Klasse 6, 7, 8, 9, 10 (Gymnasium Brandenburg). Cornelsen, 2008 (Đức).
2. Algebra 1, 2. Holt McDougal 2011 (Mĩ).
3. New Mathematics Counts 3,4,5. Federal Publications 2004, (Singapore).
4. Mathematics quyển 1 (thượng, hạ), quyển 2 (thượng, hạ). People Education Press, 2002 (Trung Quốc).
5. Core Mathematics 2 unit C2. Edexcel 2012 (Anh).
6. Mathematics Higher Level (Core). International Baccalaureate, 1999 (Australia).
7. Toán 6 ,7, 8, 9 (tập 1, 2). NXBGDVN 2010 (Việt Nam).
8. Đại số 10, Đại số và Giải tích 11, Giải tích 12. NXBGDVN, 2010 (Việt Nam).
9. Đại số 10 Nâng cao (NC), Đại số và Giải tích 11 NC, Giải tích 12 NC. NXBGDVN, 2010
(Việt Nam).
10. Hình học 10, 11, 12. NXBGDVN, 2010 (Việt Nam).
11. Hình học 10NC, 11NC, 12NC. NXBGDVN, 2010 (Việt Nam).
12. IGCSE Mathematics, Cambridge University Press 2010 (Anh).
13. Common Core State Standards for Mathematics, Common Core State Standards Initiative (preparing America’s students for college & career) (Mĩ).
* Nhà xuất bản Giáo dục Việt Nam.