Chứng minh hình thang là một kỹ năng quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về các tính chất hình học của tứ giác. Hãy cùng khám phá các cách chứng minh thông qua các bước đơn giản và hiệu quả mà Học Thế Nào giới thiệu trong bài viết dưới đây!
Khái quát về hình thang
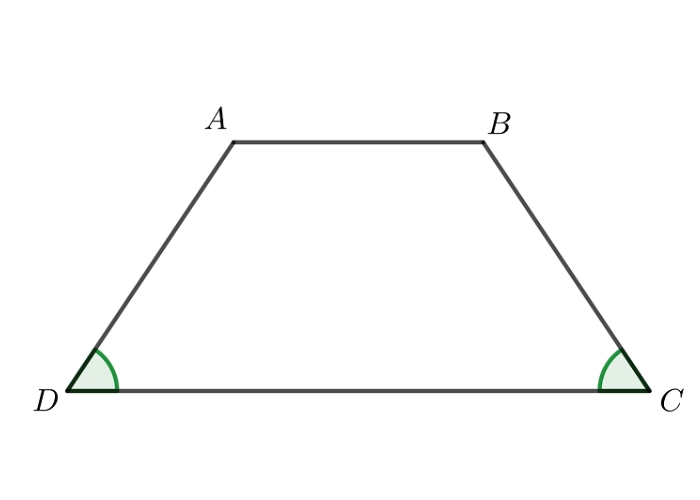
Hình thang là một loại tứ giác có hai cặp cạnh song song với nhau. Hai cạnh này được gọi là cạnh đáy, trong khi hai cạnh còn lại được gọi là cạnh bên. Dựa trên các đặc điểm về góc và đối xứng, hình thang có thể được phân loại thành các loại như hình thang cân, hình thang vuông.
Xem ngay: Hình thang là gì? Tính chất, đặc điểm của hình thang
Dấu hiệu nhận biết hình thang đơn giản nhất
Dấu hiệu nhận biết hình thang:
- Một tứ giác có hai cạnh đối diện song song là hình thang.
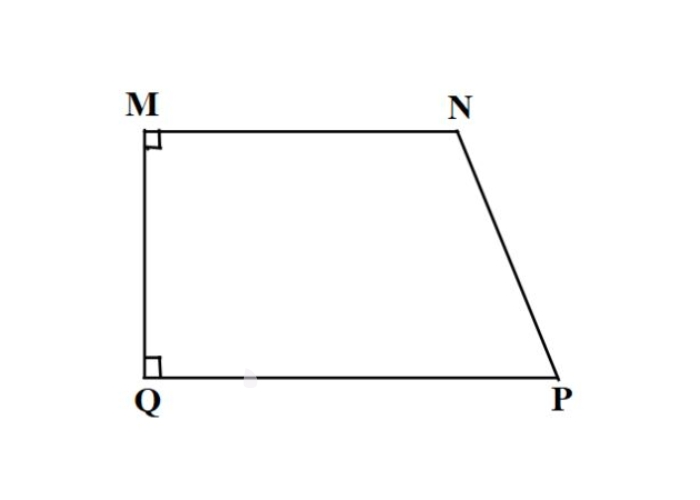
Dấu hiệu nhận biết hình thang vuông:
- Tứ giác có hai cạnh đối diện song song và một góc vuông 90 độ là hình thang vuông.
- Hình thang có một góc vuông là hình thang vuông.
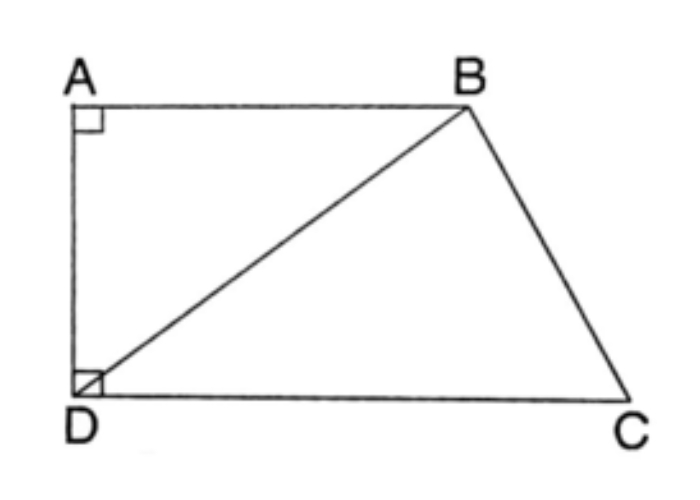
Dấu hiệu nhận biết hình thang cân:
- Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.
- Hình thang có hai đường chéo bằng nhau là hình thang cân.
Đọc ngay: Có bao nhiêu dấu hiệu nhận biết hình thang? Mẹo nhận biết đơn giản nhất
3 cách chứng minh hình thang thường dùng
Để chứng minh hình thang, bạn có thể vận dụng một trong ba cách sau:
Chứng minh bằng cạnh đối song song
Để xác định một tứ giác là hình thang có các cạnh đối diện song song, ta cần làm như sau:
- Bước 1: Xác định tứ giác cần kiểm tra, ví dụ như tứ giác ABCD.
- Bước 2: Tìm hai cặp cạnh đối diện của tứ giác và kiểm tra xem chúng có song song với nhau không, ví dụ AB và CD.
- Bước 3: Sử dụng các định lý về đường thẳng song song để chứng minh. Ví dụ, nếu hai đường thẳng cắt một đường thẳng thứ ba sao cho các góc so le trong bằng nhau, thì hai đường thẳng đó là đường song song.
=> Kết luận: Nếu có thể chứng minh rằng cặp cạnh AB và CD của tứ giác ABCD là 2 đường thẳng song song, thì tứ giác đó là hình thang.
Chứng minh bằng đường trung bình
Đường trung bình của hình thang là dụng cụ hữu ích để kiểm tra tứ giác có phải là hình thang hay không. Dưới đây là cách chứng minh đơn giản:
- Chứng minh tính song song: Để kiểm tra tứ giác là hình thang, bạn cần chứng minh rằng đường trung bình chạy song song với cạnh đáy. Sử dụng các quy tắc về đường song song để chứng minh điều này.
- Chứng minh độ dài đường trung bình: Bằng cách tính toán, bạn chứng minh rằng độ dài của đường trung bình bằng một nửa tổng hai cạnh đáy. Khi hai cạnh đối diện chạy song song với nhau thì tứ giác đó trở thành hình thang.
Cách chứng minh hình thang bằng tính chất góc
Để chứng minh một tứ giác là hình thang, bạn có thể áp dụng phương pháp sau:
- Bước 1: Vẽ tứ giác ABCD và giả sử nó là hình thang.
- Bước 2: Xác định hai góc kề một cạnh bên, chẳng hạn cạnh AD, và gọi chúng là góc A và góc D.
- Bước 3: Chứng minh rằng tổng hai góc A và D bằng 180 độ bằng cách sử dụng các quy tắc về góc trong hình học.
- Bước 4: Thực hiện tương tự cho cặp góc ở cạnh đối diện.
Ví dụ: Chứng minh rằng góc AEB và góc CFD cùng bằng 90 độ do tính chất của giao điểm.
Từ đó suy ra tổng của các góc trong cặp góc kề bên đều bằng 180 độ.
=> Kết luận: Nếu tổng của hai góc kề một cạnh bên bằng 180 độ, tứ giác ABCD là hình thang.
Tham khảo ngay: Tính chất đường chéo hình thang là gì?
Bài tập minh hoạ chứng minh hình thang
Để chứng minh một tứ giác có phải là hình thang hay không, bạn có thể thực hiện bằng nhiều phương pháp khác nhau. Dưới đây là hai ví dụ minh họa cách chứng minh một tứ giác bất kỳ là hình thang, sử dụng tính chất đường trung bình và tổng hai góc kề một cạnh.
Ví dụ 1: Chứng minh bằng đường trung bình
Giả sử đề cho tứ giác ABCD, yêu cầu chứng minh đó là hình thang.
Cách làm
- Bước 1: Xác định rằng MN là đường trung bình của tứ giác, với M và N lần lượt là trung điểm của AD và BC.
- Bước 2: Chứng minh MN song song với AB và CD, và có độ dài bằng nửa tổng AB và CD.
- Bước 3: MN song song và bằng nửa tổng hai cạnh đối diện là bằng chứng cho thấy ABCD là hình thang.
Ví dụ 2: Chứng minh bằng tổng hai góc kề một cạnh
Xét tứ giác ABCD, trong đó đề yêu cầu chứng minh rằng đây là hình thang.
Cách làm
- Bước 1: Chứng minh rằng tổng góc A và góc D bằng 180 độ, tức là tổng hai góc kề một cạnh của hình thang.
- Bước 2: Vì tổng hai góc này bằng 180 độ, theo định nghĩa, tứ giác ABCD là hình thang.
Xem thêm: Công thức tính diện tích hình thang chi tiết nhất
Mẹo giải bài toán chứng minh hình thang
Để giải bài toán chứng minh một tứ giác là hình thang, có một số mẹo hữu ích như sau:
- Xác định các cạnh đối diện song song: Luôn kiểm tra xem 2 cặp cạnh đối diện mà bạn nghi ngờ xem chúng có song song với nhau hay không. Điều này là bước quan trọng để giảm bớt phạm vi của bài toán.
- Sử dụng định lý Thales: Định lý Thales cho phép chứng minh rằng nếu hai đoạn thẳng song song bị cắt bởi một đường thẳng bất kỳ, các đoạn thẳng chéo tương ứng trên đường thẳng đó sẽ có tỉ lệ bằng nhau. Áp dụng định lý Thales để chứng minh hai cặp cạnh đối diện là song song.
- Chứng minh tổng góc: Kiểm tra tổng các góc kề một đáy của tứ giác. Nếu tổng các góc này bằng 180 độ, tứ giác có khả năng là hình thang.
- Chứng minh tổng các góc đối diện: Chứng minh rằng tổng của các góc đối diện của tứ giác bằng 360 độ. Điều này cũng là một trong các điều kiện cần để chứng minh tứ giác là hình thang.
- Sử dụng đường trung bình: Chứng minh đường chéo chia tứ giác ra làm thành 2 hình tam giác nhỏ tương đồng nhau. Đặc biệt, nếu 2 đường chéo trong hình tứ giác cắt nhau và cùng tạo thành những tỉ lệ bằng nhau thì đó là hình thang.
Tính ứng dụng của hình thang trong thực tiễn
Hình thang có nhiều ứng dụng trong thực tiễn do tính chất hình học đặc biệt của nó. Dưới đây là một số ví dụ về các ứng dụng này:
- Thiết kế cầu đường: Hình thang được sử dụng trong thiết kế cầu, đường và các công trình xây dựng để đảm bảo tính cân bằng, ổn định.
- Trang trí nội thất: Hình thang được áp dụng trong thiết kế nội thất, chẳng hạn như các mặt bàn, kệ sách, hay các vật dụng trang trí có dạng hình thang.
- Thiết kế máy móc: Nhiều bộ phận của máy móc và công cụ có dạng hình thang để đảm bảo tính ổn định và hiệu quả khi hoạt động.

Trên đây là toàn bộ những cách chứng minh hình thang mà bạn cần biết. Hy vọng bài viết đã giúp bạn nắm được phương pháp làm bài cũng như biết cách ứng dụng vào trong đời sống thực tiễn. Đừng quên theo dõi thêm các bài viết khác để cập nhật nhiều bài học bổ ích bạn nhé!