Tính diện tích hình tam giác cân là dạng toán cơ bản mà bạn sẽ được học trong chương trình Tiểu học. Công thức này áp dụng nhiều trong thực tế để tính diện tích của một mảnh đất hoặc đồ vật có hình dạng tam giác cân. Bài viết sau sẽ giúp bạn hiểu rõ hơn cách tính S của tam giác cân thông qua ví dụ minh họa.
Giới thiệu đôi nét về tam giác cân
Trước hết, bạn cần hiểu tgc là gì. Tam giác cân là hình tam giác có 2 cạnh bên và 2 góc đáy bằng nhau, đỉnh là giao điểm của 2 cạnh bên. Đường trung trực từ đỉnh cân của tam giác cân trùng với đường trung tuyến cạnh đối diện và cũng là đường cao từ đỉnh đó. Để phân loại tam giác cân có thể dựa vào số đo góc đỉnh, bao gồm:
- Tam giác vuông cân: Góc giữa 2 cạnh bên là 90 độ, các góc khác 45 độ.
- Tam giác nhọn cân: Hình có cả 3 góc đều nhỏ hơn 90 độ.
- Tam giác tù cân: Có 1 góc lớn hơn 90 độ.
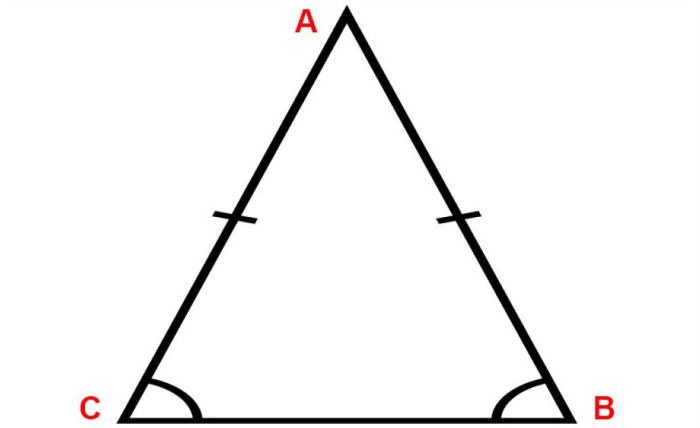
Công thức tính diện tích hình tam giác cân
Để tính diện tích tam giác cân, bạn cần học thuộc và hiểu được công thức. Học sinh cấp 1 chỉ được giáo viên giới thiệu cách tính cơ bản, học tới các lớp THCS, THPT bạn sẽ được dạy công thức nâng cao để tính được diện tích của nhiều loại hình tam giác cân khác nhau.
Công thức cơ bản
Diện tích của một tam giác cân bằng độ dài đáy nhân với chiều cao rồi chia cho 2. $$S\;hình\;tam\;giác\;cân\;=\;\frac12a\;\times\;h$$
Trong đó:
- S: ký hiệu diện tích
- a: độ dài cạnh đáy
- h: độ dài đường cao
Cách tính diện tích hình tam giác cân nâng cao
Với công thức cơ bản, bạn cần biết độ dài cạnh đáy và đường cao hình tam giác cân mới tính được diện tích. Nếu bài toán chỉ cho sẵn độ dài 2 cạnh và góc xen giữa, bạn có thể áp dụng công thức nâng cao. Cụ thể: “Cách tính diện tích hình tam giác cân sẽ bằng tích độ dài 2 cạnh nhân với sin góc xen giữa sau đó chia cho 2”. $$S\;hình\;tam\;giác\;cân\;=\;\frac12\;a\;\times\;b\;\times\;\sin(C)\;=\;\;\frac12\;a\;\times\;c\;\times\;\sin(B)\;=\;\frac12\;b\;\times\;c\;\times\;\sin(A)$$
Trong đó:
- S: ký hiệu diện tích
- a, b, c : độ dài các cạnh
- C: góc xen giữa 2 cạnh a và b
- B: góc xen giữa 2 cạnh a và c
- A: góc xen giữa 2 cạnh b và c
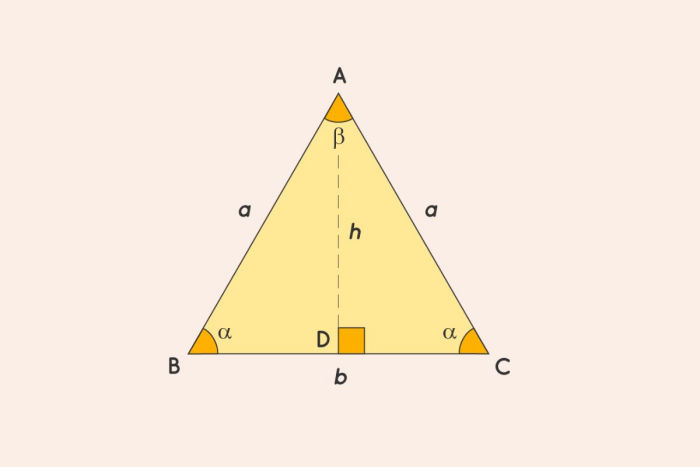
Trường hợp cần sử dụng công thức nâng cao tiếp theo khi tính diện tích tam giác cân là đề bài đã cho hết 2 góc và độ dài các cạnh. $$S\;tam\;giác\;cân\;=\;\lbrack a^2\times\sin(\beta)\times\sin(\alpha)/2\times\sin(2\mathrm\pi-\alpha-\beta)\rbrack$$
Trong đó:
- S: ký hiệu diện tích
- a: số đo 2 cạnh bằng nhau
- b: số đo cạnh đáy
- α: số đo 2 góc bằng nhau
- β: số đo góc còn lại
Xem thêm: Cách tính chu vi hình tam giác cân
Một số bài toán về diện tích tgc
Để hiểu rõ hơn về cách tính diện tích tgc, bạn hãy tham khảo các ví dụ minh họa sau. Ví dụ được đưa ra dựa theo từng công thức cơ bản và nâng cao.
Bài 1: Cho hình tam giác cân ABC có AB = AC = 6cm, BC = 8cm. Tính diện tích hình tgc ABC.
Với đề bài này, chúng ta sẽ sử dụng công thức cơ bản: $$S\;=\;\frac12\;a\;\times\;h$$
Bài giải: Diện tích hình tgc ABC: $$S\;=\;AB\;\times\;BC\;/\;2\;=\;6\;\times\;8\;/\;2\;=\;24\;cm^2.$$
Bài 2: Cho hình tam giác cân ABC có độ dài cạnh AB = AC = 4cm, góc BAC = 45 độ. Tính diện tích của tam giác cân ABC.
Đề bài trên sử dụng công thức: $$S\;=\;\frac12\;a\;\times\;b\;\times\;\sin(C)$$
Bài giải: Diện tích một tam giác cân ABC: $$S\;=\;\frac12\;\times\;AB\;\times\;AC\;\times\;Sin(BAC)\;=\;4\;\times\;4\;\times\;\sin\;(45)\;=\;4\;cm^2.$$
Bài 3: Cho hình tam giác cân ABC có độ dài AB = AC = 5cm, BC = 8cm, góc ABC = ACB = 45 độ, góc BAC = 90 độ. Tính diện tích của tam giác cân.
Với đề bài này, chúng ta sử dụng công thức $$S\;tam\;giác\;cân\;=\;\lbrack a^2\times\sin(\beta)\times\sin(\alpha)/2\times\sin(2\mathrm\pi-\alpha-\beta)\rbrack$$.
Bài giải: Diện tích hình tam giác ABC: $$S\;=\;\lbrack52\;\times\;\sin(90)\;\times\;\sin(45)/2\;\times\;\sin\;(2\mathrm\pi\;-\;90\;-\;45)\rbrack=\;6,89\;cm^2.$$
Tìm hiểu thêm: Cách làm dạng toán chứng minh tam giác cân.
Ứng dụng của việc tính dt hình tam giác cân trong thực tế
Công thức tính dt hình tam giác cân không chỉ áp dụng trong toán học mà còn được ứng dụng trong thực tế. Dưới đây là những lĩnh vực yêu cầu bạn cần phải biết cách tính diện tích hình học:
- Xây dựng: Tam giác cân được sử dụng để thiết kế cấu trúc mái vòm và trang trí trong công trình. Người kiến trúc sư cần biết cách tính S hình tam giác cân để thiết kế đúng tỷ lệ.
- Thiết kế đồ họa: Tam giác cân được sử dụng để thiết kế trang phục, đồ vật có tính thẩm mỹ cao và người thiết kế cần phải tính được diện tích của nó.
- Nghiên cứu khoa học: Nhà khoa học ứng dụng cách tính dt hình tam giác cân vào các hoạt động nghiên cứu toán học và khoa học.
- Sản xuất máy móc, trang thiết bị: Các bộ phận trong máy móc, thiết bị công nghiệp áp dụng tam giác cân trong thiết kế và cách tính diện tích để đảm bảo vận hành ổn định.

Công thức tính diện tích hình tam giác cân được ứng dụng trong nhiều lĩnh vực của đời sống xã hội. Hy vọng qua những thông tin trên, bạn đọc đã hiểu rõ cách tính diện tích để áp dụng vào việc học tập hoặc công việc. Nếu muốn ôn lại những công thức tính khác, hãy tiếp tục theo dõi những bài viết sau nhé.