Cách tính diện tích hình tròn là công thức toán học quan trọng và được ứng dụng phổ biến trong nhiều lĩnh vực khác nhau, từ học thuật đến thực tiễn cuộc sống. Cùng theo dõi bài viết dưới đây để nắm rõ về công thức này.
Công thức tính diện tích hình tròn
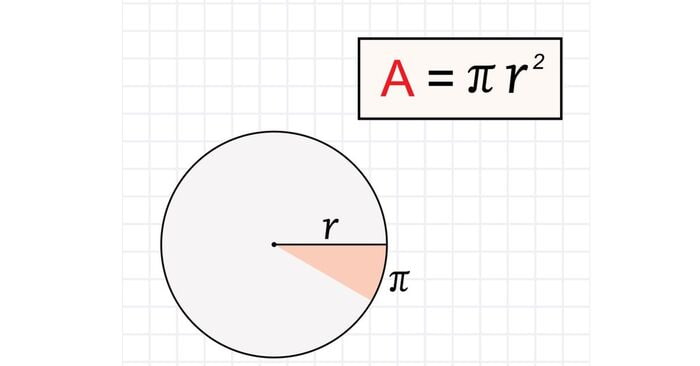
Diện tích của một hình tròn được tính toán như sau:
$$A=\mathrm\pi\times\mathrm r^2$$
Trong đó:
- A là diện tích của hình tròn
- r là bán kính hình tròn
- π là một hằng số toán học, có giá trị xấp xỉ 3,14159.
Dựa vào công thức này, các bạn có thể dễ dàng tính dt của bất kỳ ht nào khi biết được bán kính của nó.
Tham khảo: ht là gì? giúp bạn hiểu rõ về đặc điểm, tính chất của hình tròn
Lịch sử phát triển công thức diện tích hình tròn
Việc tính diện tích của đường đã được ứng dụng từ rất sớm, vào thế kỷ 5 trước Công Nguyên từ nhà toán học người Hy Lạp là Eudoxus của Cnidus, người đã nhận ra mối liên hệ đặc biệt giữa bình phương bán kính của ht và diện tích của nó.
Sau đó, nhà toán học Archimedes vĩ đại đã tiếp tục phát triển công trình này bằng cách sử dụng phương pháp exhaust để chứng minh dtcủa ht bằng bình phương bán kính nhân với một hệ số không đổi π.
Ta có công thức tính dt hình tròn: $$A=\mathrm\pi\times\mathrm r^2$$
Đây bước ngoặt quan trọng trong lịch sử phát triển toán học, khi người ta đã tìm ra cách tính diện tích của hình tròn và công thức này có rất nhiều ứng dụng quan trọng trong thực tiễn khoa học, kỹ thuật.

Ví dụ bài tập minh họa cách tính diện tích hình tròn
Để hiểu rõ về cách tính diện tích của hình tròn, mời các bạn theo dõi ví dụ dưới đây:
Ví dụ minh họa: Tính dt hình tròn khi biết bán kính r = 4 cm.
Hướng dẫn giải:
- Bước 1: Xác định bán kính của ht cần tính, ở đây r = 4 cm.
- Bước 2: Áp dụng công thức tính diện tích hình tròn là A = π.r^2.
- Bước 3: Thay số liệu cụ thể của bài toán vào công thức, ta được A = π.4^2 = 16.π
- Bước 4: Tính toán đưa ra kết quả cuối cùng, lấy pi xấp xỉ 3,14 ta được A = 16.3,14 = 50,24 cm^2.
Kết luận: Diện tích của hình tròn cần tìm là 50,24 cm^2.
Đừng bỏ qua cách tính chu vi hình tròn chi tiết và chuẩn xác
Mẹo nhớ công thức tính diện tích hình tròn
Để nhớ công thức tính diện tích hình tròn, bạn có thể sử dụng một số mẹo sau đây:
- Ghi nhớ công thức cơ bản: Các bạn chỉ cần nhớ rằng dt của ht tỷ lệ thuận với bình phương của bán kính nhân với hệ số cố định π.
- Luyện tập thường xuyên: Thực hành tính diện tích của hình tròn với các giá trị bán kính khác nhau để làm quen với công thức và ghi nhớ nó lâu dài.
- Ghi nhớ liên kết với chu vi: Nhớ rằng chu vi ht được tính bằng công thức C=2πr và dt là πr^2. Sự liên kết này có thể giúp bạn nhớ công thức dễ dàng hơn.
Một số dạng bài tập về diện tích hình tròn
Dưới đây là một số dạng bài tập phổ biến về diện tích của đường tròn thường xuất hiện trong bài thi:
So sánh diện tích hai hình tròn
Đây là một dạng bài khá đơn giản, bạn chỉ cần áp dụng công thức và tính dt của hình tròn, sau đó đem so sánh là có thể giải quyết nhanh chóng. Tuy nhiên, cần đảm bảo sự thống nhất về đơn vị đo của bán kính, nếu dữ liệu đề bài đưa ra chưa thống nhất thì cần phải đổi lại.
Ví dụ minh họa: So sánh diện tích của hai hình tròn sau:
- Hình tròn có S1 có diện tích là 12 cm2
- Hình tròn S2 có diện tích là 1300 cm2
Hướng dẫn giải:
Ta thực hiện quy đổi diện tích của S2 sang cm2: 1300 mm2 = 13 cm2. Suy ra S2 > S1.
Tính diện tích hình tròn khi biết bán kính hoặc đường kính
Ở dạng bài này, bạn chỉ cần áp dụng công thức như bình thường nếu đề bài cho bán kính. Trường hợp cho biết đường kính D, bạn tính r = D/2 rồi áp dụng công thức như bình thường.
Ví dụ minh họa:
Cho hình tròn C có đường kính D = 10 cm. Hãy tính S hình tròn C?
Hướng dẫn giải:
Ta có: R = D/2 = 10/2 = 5 cm.
S hình tròn của C: S = π.r^2 = 3,14.5^2 = 78,5 cm2
Tính diện tích hình vành khăn
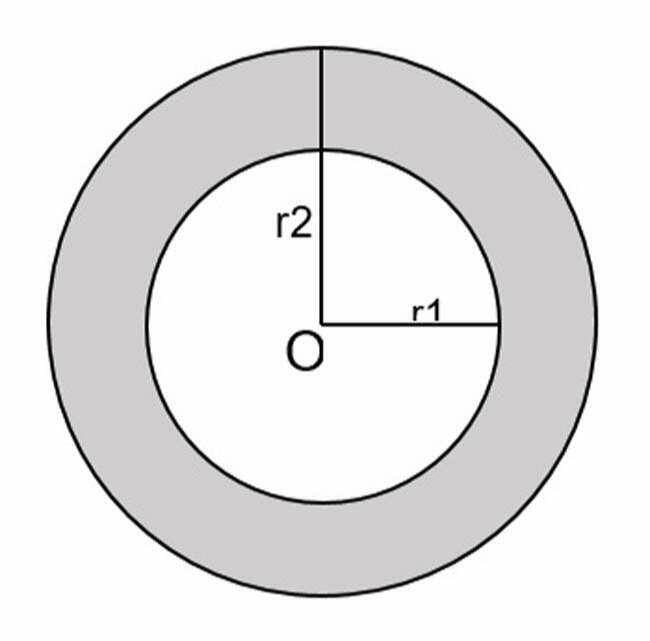
Ở dạng này, đề bài sẽ cho một hình tròn lớn chứa bên trong là ht nhỏ có đầy đủ dữ liệu về bán kính của 2 hình tròn này. Yêu cầu đề bài sẽ là tính phần vành khăn hay phần nằm giữa hình tròn lớn và ht nhỏ.
Ví dụ minh họa: Cho hình vẽ như dưới, biết đường tròn lớn có r2 = 20 cm và hình tròn nhỏ có r1 = 10 cm. Tính phần diện tích của hình tròn màu xám trong hình vẽ.
Hướng dẫn giải:
Ta thấy, diện tích vòng tròn màu xám = S(r2) – S(r1)
Ta tính: S(r2) = π.(r2)^2 = 3,14.20^2 = 1256 cm2
Và S(r1) = π.(r1)^2 = 3,14.10^2 = 314 cm2
Từ đây ta có: Diện tích của vành khăn màu xám = 1256 – 314 = 942 cm2.
Đề này khá đơn giản, chỉ cần áp dụng công thức là tính được. Tuy nhiên, các bạn cần lưu ý về sự thống nhất trong đơn vị đo của bán kính.
Tính diện tích hình bất kỳ có chứa 1 phần diện tích hình tròn
Đây là một dạng bài nâng cao, các bạn cần nắm vững kiến thức về công thức tính diện tích của các hình khác nhau, sau đó áp dụng và đưa ra kết quả cuối cùng theo yêu cầu đề bài.
Ví dụ minh họa: Tính diện tích toàn bộ hình như bên dưới.
Theo đề bài cho ta có tổng diện tích hình bên dưới bằng dt của hình chữ nhật kích thước 8 x 4 cm và dt của 2 nửa hình tròn có bán kính là r = 4 cm.
Như vậy, diện tích hình chữ nhật là S1 = 8 x 4 x 2 = 64 cm2.
Diện tích 2 nửa hình tròn bán kính r là S2 = 3,14.4^2 = 50,24 cm2
=> S toàn bộ hình = S1 + S2 = 64 + 50,24 = 114,24 cm2.
Bài toán tính diện tích hình tròn từ đường kính (Nâng cao)
Với dạng bài toán nâng cao về dt hình tròn, tùy vào dữ đề bài mà các bạn xem xét và đưa ra cách tính diện tích hình tròn chuẩn xác.
Ví dụ minh họa: Tính dt của dường tròn (S), biết nếu tăng đường kính hình tròn lên 30% thì dt hình tròn tăng thêm 20 cm2.
Hướng dẫn giải:
Trường hợp tăng đường kính hình tròn lên 30% thì bán kính của nó cũng tăng thêm 30%.
=> Số % diện tích được tăng thêm là:
$$(130\%)^2-(100\%)^2=69\%.$$
Vậy diện tích của hình tròn ban đầu cần tính là: 20.100/69 = 29,956 cm2.
Ứng dụng của diện tích hình tròn trong thực tế
Tương tự như các hình học khác, công thức tính diện tích của hình tròn được ứng dụng rộng rãi trong nhiều lĩnh vực tử khoa học, kỹ thuật cho đến nghệ thuật và giáo dục. Kiến thức này giúp các kỹ sư tính toán và phát triển nhiều vật dụng sử dụng trong cuộc sống hàng ngày một cách chuẩn xác, đem lại hiệu quả sử dụng cao.

Hy vọng những chia sẻ trên đây của chúng tôi sẽ giúp các bạn hiểu rõ về công thức tính diện tích hình tròn chuẩn xác, các dạng bài tập thường xuất hiện trong bài thi và vai trò của chúng trong cuộc sống hàng ngày. Đừng quên theo dõi bài viết khác của chúng tôi để cập nhật nhiều kiến thức bổ ích nhé!