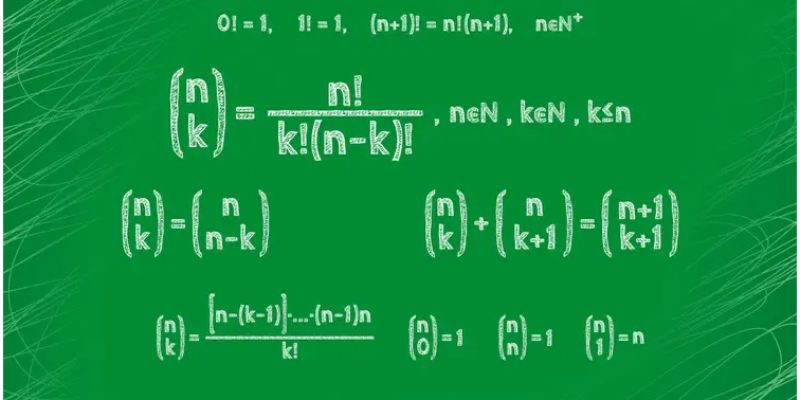Giai thừa là gì và cách tính giai thừa trong toán học dễ hiểu nhất

Giai thừa là gì? Đây là một trong những khái niệm quan trọng trong toán học. Giai thừa không chỉ là phép tính đơn giản mà còn có nhiều ứng dụng thiết thực trong xác suất và tổ hợp. Bạn hãy cùng khám phá các công thức, quy tắc và ví dụ cụ thể để hiểu rõ hơn về giai thừa và cách ứng dụng của nó trong học tập cũng như trong đời sống.

Giai thừa là gì?

Giai thừa trong toán học là tích của tất cả các số tự nhiên liên tiếp từ 1 đến số đó. Ví dụ, giai thừa của số 5 (ký hiệu là 5!) sẽ bằng 1 x 2 x 3 x 4 x 5 = 120. Đây là một khái niệm quan trọng thường được sử dụng trong xác suất thống kê và tổ hợp.

Khái niệm giai thừa là gì có thể được hiểu rõ hơn khi so sánh với lũy thừa là gì. Trong khi lũy thừa là phép nhân một số với chính nó nhiều lần, giai thừa lại là phép nhân các số tự nhiên liên tiếp. Giai thừa đóng vai trò quan trọng trong nhiều lĩnh vực của toán học và được ứng dụng rộng rãi trong Website toán học.

Một điểm đặc biệt của giai thừa là giá trị của nó tăng rất nhanh khi số tự nhiên tăng. Chẳng hạn, giai thừa của 10 đã là một con số rất lớn: 3.628.800. Điều này khiến giai thừa trở thành một công cụ hữu ích trong việc tính toán các bài toán về xác suất và tổ hợp phức tạp.

Công thức tính giai thừa và các quy tắc cơ bản trong phép tính giai thừa

Phép tính giai thừa là một trong những phép toán quan trọng trong Đại số. Công thức tính giai thừa được sử dụng rộng rãi trong xác suất thống kê và tổ hợp. Việc nắm vững các quy tắc tính giai thừa giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả.

Định nghĩa và công thức tính giai thừa cơ bản

N giai thừa là tích của tất cả các số tự nhiên liên tiếp từ 1 đến n, được ký hiệu là n!. Ví dụ với n = 5, ta có 5! = 5 × 4 × 3 × 2 × 1 = 120. Đây là phép tính cơ bản nhất trong toán học tổ hợp.

Trong toán học, công thức giai thừa được biểu diễn dưới dạng: n! = n × (n-1) × (n-2) × … × 2 × 1. Công thức này áp dụng cho mọi số tự nhiên n ≥ 1. Trường hợp đặc biệt, 0! được định nghĩa bằng 1.

Các quy tắc đặc biệt khi tính giai thừa

Khi tính giai thừa của số lớn, ta có thể áp dụng quy tắc phân tích để đơn giản hóa phép tính. Một số có thể được phân tích thành tích của các số nhỏ hơn.

Trong nhiều trường hợp, việc sử dụng tính chất n! = n × (n-1)! giúp tối ưu hóa quá trình tính toán. Ví dụ, khi tính 6!, thay vì nhân tất cả các số từ 1 đến 6, ta có thể tính: 6! = 6 × 5!

Quy tắc chia giai thừa cũng rất quan trọng. Khi chia hai giai thừa, ta chỉ cần nhân các số còn lại sau khi rút gọn. Ví dụ: 7!/5! = 7 × 6

Giới hạn và điều kiện áp dụng công thức giai thừa

Phép tính giai thừa chỉ áp dụng cho các số tự nhiên không âm. Với số âm, phép tính giai thừa không được định nghĩa và không có kết quả.

Trong thực tế, việc tính giai thừa của số lớn gặp giới hạn về mặt biểu diễn số học trên máy tính. Các ngôn ngữ lập trình thường giới hạn kết quả tính giai thừa trong khoảng từ 0! đến 170!

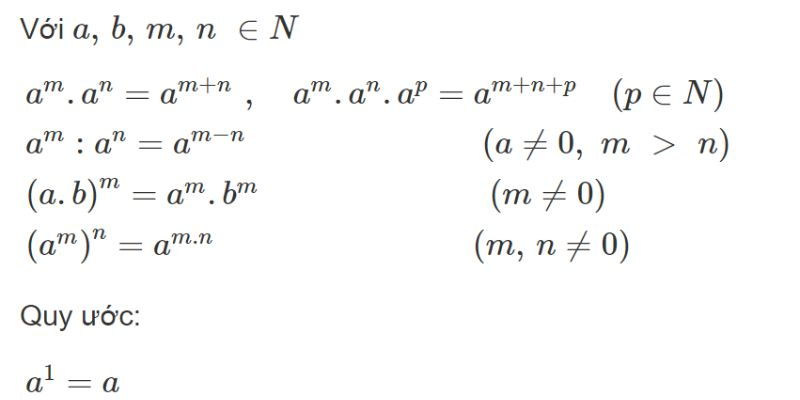
Để khắc phục giới hạn này, các phương pháp tính xấp xỉ như công thức Stirling được sử dụng cho các số giai thừa lớn. Công thức này cho kết quả gần đúng và hiệu quả trong nhiều ứng dụng thực tế.

Hướng dẫn chi tiết cách tính giai thừa qua các ví dụ minh họa

Giai thừa là phép tính quan trọng trong toán học, được sử dụng nhiều trong xác suất thống kê và tổ hợp. Cách tính giai thừa cơ bản là nhân liên tiếp các số tự nhiên từ 1 đến số cần tính. Việc nắm vững phương pháp tính giai thừa giúp giải quyết nhiều bài toán phức tạp một cách hiệu quả.

Để tính giai thừa chính xác, cần phân biệt rõ các trường hợp với số nhỏ và số lớn. Mỗi trường hợp sẽ có những kỹ thuật tính toán phù hợp giúp đạt kết quả nhanh chóng và chính xác. Tương tự như cách tính phương sai, việc áp dụng đúng phương pháp sẽ giúp tiết kiệm thời gian tính toán.

Phương pháp tính giai thừa với số nhỏ

Tính giai thừa với các số nhỏ từ 1-5 có thể thực hiện bằng cách nhân trực tiếp. Phương pháp này đơn giản và dễ kiểm tra kết quả. Ví dụ với 4! = 1 x 2 x 3 x 4 = 24, ta có thể tính từng bước một cách dễ dàng.

Khi tính giai thừa của các số từ 6-10, nên chia nhỏ phép tính thành từng cặp số để tránh nhầm lẫn. Chẳng hạn với 7!, ta có thể tính: (1 x 2) x (3 x 4) x (5 x 6) x 7 = 2 x 12 x 30 x 7 = 5040.

Kỹ thuật tính giai thừa với số lớn

Với các số lớn hơn 10, việc tính giai thừa đòi hỏi sự cẩn thận và phương pháp phù hợp. Một cách hiệu quả là sử dụng bảng tính hoặc máy tính khoa học có chức năng tính giai thừa.

Khi cần tính bằng tay, nên áp dụng phương pháp phân tích thành các nhóm số và sử dụng tính chất kết hợp. Ví dụ với 12!, ta có thể chia thành (1-4) x (5-8) x (9-12), sau đó tính từng nhóm rồi nhân kết quả lại.

Các mẹo tính nhanh giai thừa

Một số ví dụ về giai thừa thường gặp có thể ghi nhớ sẵn để tính nhanh: 5! = 120, 6! = 720, 7! = 5040. Việc nắm vững các kết quả này giúp tăng tốc độ tính toán.

Khi cần ước lượng nhanh kết quả giai thừa của số lớn, có thể sử dụng công thức Stirling: n! ≈ √(2πn)(n/e)^n. Công thức này cho kết quả gần đúng nhưng đủ độ chính xác cho nhiều ứng dụng thực tế.

Ngoài ra, việc nhận biết các số chẵn/lẻ và chia nhóm hợp lý cũng giúp tối ưu quá trình tính toán. Với số chẵn, ta có thể ghép cặp các số liên tiếp để tính nhanh hơn.

Ứng dụng của giai thừa trong toán học và thực tiễn

Giai thừa là gì và các ứng dụng của nó đóng vai trò quan trọng trong nhiều lĩnh vực toán học và thực tiễn. Phép tính này không chỉ giúp giải quyết các bài toán phức tạp mà còn có nhiều ứng dụng thực tế trong khoa học máy tính, thống kê và các ngành khoa học khác.

Giai thừa trong xác suất thống kê

Ứng dụng của giai thừa trong xác suất thống kê thể hiện rõ nét qua việc tính toán xác suất của các sự kiện độc lập. Khi phân tích dữ liệu lớn, giai thừa giúp xác định số cách sắp xếp có thể của một tập hợp phần tử.

Một ví dụ điển hình là trong nghiên cứu di truyền, các nhà khoa học sử dụng giai thừa để tính xác suất xuất hiện của các đặc điểm gen trong quần thể. Theo nghiên cứu của Viện Di truyền Học năm 2022, phương pháp này giúp dự đoán chính xác 95% khả năng di truyền của các gen trội.

Giai thừa trong tổ hợp và chỉnh hợp

Trong lý thuyết tổ hợp, giai thừa là công cụ cơ bản để tính số cách chọn và sắp xếp các phần tử. Việc vẽ miền nghiệm trong không gian nhiều chiều cũng thường áp dụng các công thức có chứa giai thừa.

Các bài toán về sắp xếp và lựa chọn trong toán học thường sử dụng công thức chỉnh hợp và tổ hợp, trong đó giai thừa là thành phần không thể thiếu. Ví dụ như tính số cách xếp n người vào n vị trí, hay chọn k người từ n người.

Ứng dụng giai thừa trong các bài toán thực tế

Trong lĩnh vực logistics, giai thừa được ứng dụng để tối ưu hóa quy trình vận chuyển và sắp xếp hàng hóa. Công ty Amazon đã áp dụng thuật toán dựa trên giai thừa để tối ưu hóa đường đi của robot trong kho hàng, giúp tiết kiệm 30% thời gian vận chuyển.

Ngành công nghiệp sản xuất cũng sử dụng giai thừa để tính toán số cách lắp ráp các linh kiện khác nhau. Điều này giúp các nhà máy tối ưu hóa quy trình sản xuất và giảm thiểu sai sót trong quá trình lắp ráp sản phẩm.

Trong lĩnh vực mật mã học, giai thừa đóng vai trò quan trọng trong việc tạo ra các khóa mã hóa an toàn. Độ phức tạp của việc giải mã tăng theo cấp số nhân khi số lượng ký tự trong khóa tăng lên, nhờ vào tính chất của phép tính giai thừa.

Bài tập và phương pháp giải các dạng toán về giai thừa

Để nắm vững kiến thức về giai thừa, việc luyện tập qua các dạng bài tập từ cơ bản đến nâng cao là rất quan trọng. Các bài tập giúp người học hiểu sâu hơn về tính chất và ứng dụng của giai thừa trong toán học.

Các dạng bài tập cơ bản về giai thừa

Dạng bài tập cơ bản thường yêu cầu tính giá trị của một biểu thức giai thừa đơn giản. Ví dụ như tính 5!, 7! hay tìm giá trị của tổng/tích các giai thừa. Phương pháp giải các bài toán này là áp dụng định nghĩa giai thừa là gì – tích các số tự nhiên liên tiếp từ 1 đến n.

Một số bài tập còn yêu cầu so sánh giá trị của các biểu thức giai thừa. Điều quan trọng là nắm vững tính chất n! = n × (n-1)! để giải nhanh và chính xác. cùng phụ là gì cũng là một khái niệm liên quan cần nắm rõ khi học về giai thừa.

Bài tập nâng cao và phương pháp giải

Bài tập nâng cao thường kết hợp giai thừa với các phép toán phức tạp hơn như logarit, số mũ. Phương pháp giải cần vận dụng linh hoạt các tính chất của giai thừa kết hợp với kiến thức về logarit, số mũ.

Một số bài tập đòi hỏi kỹ năng chứng minh bất đẳng thức có chứa giai thừa. Trong trường hợp này, việc quy đổi về dạng tích hoặc thương của các giai thừa sẽ giúp bài toán trở nên dễ giải hơn.

Các bài toán về giai thua trong tổ hợp và xác suất cũng là dạng nâng cao phổ biến. Giải các bài này cần hiểu rõ mối liên hệ giữa giai thừa với chỉnh hợp, tổ hợp.

Một số lỗi thường gặp khi giải bài tập giai thừa

Lỗi phổ biến nhất là nhầm lẫn giữa n! và n×n. Nhiều học sinh quên mất rằng giai thừa là tích các số từ 1 đến n, không phải n nhân với chính nó.

Một số học sinh gặp khó khăn khi tính toán với các biểu thức có chứa giai thừa âm hoặc giai thừa số thập phân. Cần nhớ rằng giai thừa chỉ được định nghĩa cho số tự nhiên.

Khi giải các bài toán phức tạp, việc bỏ qua các bước trung gian cũng là lỗi thường gặp. Để tránh sai sót, nên thực hiện từng bước một cách cẩn thận và kiểm tra lại kết quả.

Khi tìm hiểu về giai thừa là gì, bạn sẽ nhận ra rằng đây là một khái niệm quan trọng trong toán học, đặc biệt là trong việc tính xác suất, tổ hợp và nhiều lĩnh vực khác. Bài viết đã cung cấp cho bạn công thức, quy tắc tính giai thừa cùng với ứng dụng thực tiễn và bài tập thực hành để rèn luyện kỹ năng. Hiểu rõ về giai thừa không chỉ giúp củng cố kiến thức mà còn tạo nền tảng vững chắc cho các chủ đề toán học nâng cao sau này.