Cách chứng minh hình tam giác vuông chi tiết và hiệu quả

Chứng minh hình tam giác vuông là dạng bài tập cơ bản thường gặp trong toán học. Để chứng minh được hình theo giả thuyết của đề bài, bạn sẽ cần linh hoạt áp dụng nhiều phương pháp khác nhau.

Định nghĩa tam giác vuông

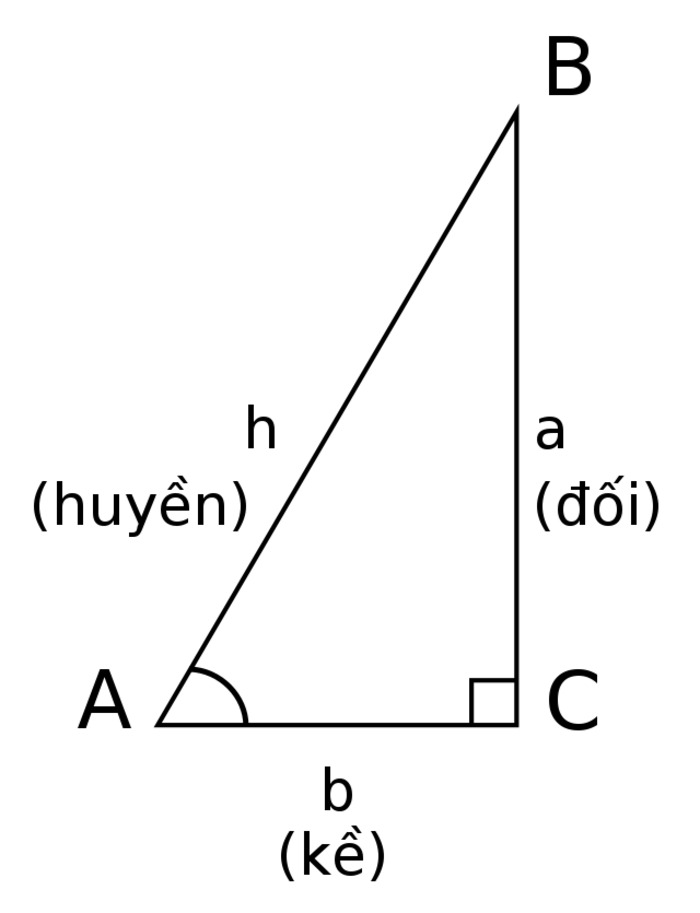
Tam giác vuông là một hình tam giác có một góc trong bằng 90 độ. Từ định nghĩa, suy ra tam giác vuông có các tính chất như sau:

• Tổng bình phương của hai cạnh góc vuông sẽ bằng bình phương của cạnh huyền.
• Hai góc nhọn có tổng bằng 90 độ.
• Hai cạnh góc vuông được coi là đường cao trong tam giác vuông.

Xem thêm: Hình tam giác cân là gì? Cách chứng minh hình tam giác cân

Cách chứng minh hình tam giác vuông chi tiết

Để chứng minh hình tam giác vuông, bạn có thể sử dụng các phương pháp sau đây:

Sử dụng định lý Pythagoras để chứng minh

Định lý này được công bố bởi nhà toán học Pythagoras từ rất lâu nhưng vẫn được áp dụng rộng rãi hiện tại. Để chứng minh tgv, định lý sẽ giúp tìm ra chiều dài của các cạnh, từ đó suy ra hình tam giác có vuông hay không.

Quy trình sử dụng định lý để chứng minh như sau:

• Xác định cạnh huyền là cạnh dài nhất trong hình tam giác.
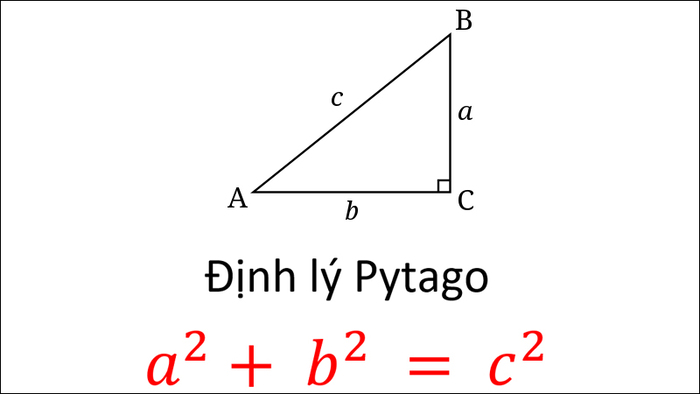
• Áp dụng công thức của định lý Pythagoras:

c² = a² + b²

Trong đó c là chiều dài cạnh huyền, a và b là chiều dài của hai cạnh góc vuông.

• Kiểm tra lại con số thực tế với công thức có khớp nhau hay không. Nếu thoả mãn thì đây là hình tam giác vuông.

Chứng minh qua các góc: Sử dụng định lý góc nhọn và góc vuông

Dựa trên các tính chất của hình tam giác vuông, ta có được cách chứng minh hình đơn giản như sau:

• Xác định các góc, bao gồm 1 góc vuông và 2 góc nhọn.
• Sử dụng định lý góc nhọn: Trường hợp hai góc nhọn trong tam giác tổng bằng 90 độ thì hình đó chính là hình tam giác vuông.
• Sử dụng công thức và chứng minh hình tam giác.

Dùng đường trung tuyến và tính chất đặc biệt của tam giác vuông

Tam giác vuông là một tam giác đặc biệt, do đó đường trung tuyến cũng sẽ có một số tính chất đặc biệt. Cụ thể là đường trung tuyến ứng với cạnh huyền sẽ bằng một nửa cạnh huyền. Phương pháp chứng minh hình tam giác vuông bao gồm các bước:

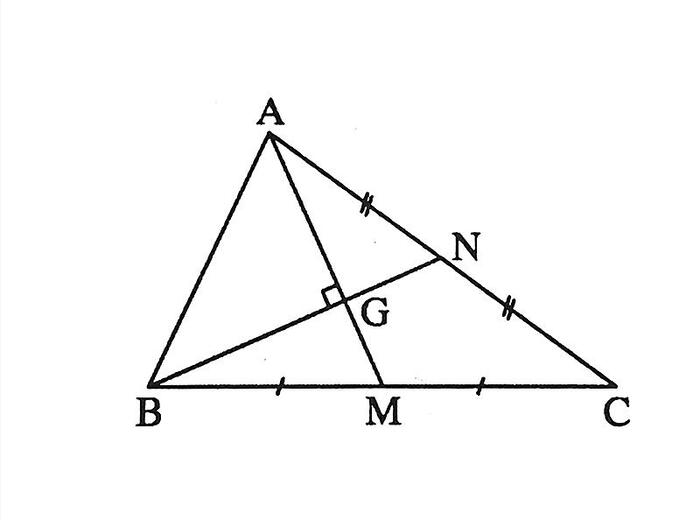
• Giả sử có hình tam giác ABC, điểm M là trung điểm của BC.
• Tính độ dài của đoạn AM.
• Nếu AM bằng một nửa của BC thì tam giác ABC là hình tam giác vuông tại A.

Xem thêm: Các cách chứng minh hình tam giác đều là gì?

Áp dụng công thức lượng giác trong tam giác

Công thức lượng giác trong số học cũng được áp dụng linh hoạt để chứng minh htg trong toán hình. Công thức này sẽ tính toán mối quan hệ của các góc và các cạnh của hình tam giác, từ đó biết được hình có vuông hay không. Cụ thể như sau:

• Định lý sin: Độ dài của cạnh đối với sin của một góc đối diện trong hình tam giác sẽ là nhất quán. Như vậy sẽ có công thức như sau:

$$\style{font-size:22px}{\frac a{\sin\;A}=\frac b{\sin\;B}=\frac c{\sin\;C}}$$

Nếu sin của một góc bằng 1 thì góc đó vuông và chứng minh được là hình tam giác vuông.

• Định lý cos: Với định lý cosin, ta có thể tính được độ dài của một cạnh dựa trên độ dài của hai cạnh còn lại và cosin góc tạo ra bởi 2 cạnh đó.

Công thức:

c² = a² + b² – 2abcosC

Nếu cosC = 0 thì công thức trên trở thành định lý Pythagoras, như vậy tam giác sẽ vuông tại góc C.

• Ứng dụng các định lý này, ta sẽ tìm được các góc của hình tam giác và chứng minh dễ dàng được đó có phải tam giác vuông hay không.

Bài tập minh họa các cách chứng minh tam giác vuông

Cho một bài tập minh hoạ cụ thể áp dụng định lý Pythagoras để chứng minh tam giác vuông như sau:

Giả sử tam giác ABC có chiều dài của 3 cạnh AB, AC, BC lần lượt là 3cm, 4cm và 5cm. Hãy chứng minh tam giác này vuông và vuông tại điểm nào.

Lời giải:

Khi đã có chiều dài của 3 cạnh tam giác, ta có thể áp dụng công thức của định lý Pythagoras. Nếu BC^2 = AC^2 + AB^2 thì ABC sẽ là tam giác vuông.

Ta có:

BC^2 = 5^2 = 25cm

AC^2 = 4^2 = 16cm

AB^2 = 3^2 = 9cm

Mà 25 = 16 + 9. Do đó chứng minh được BC^2 = AC^2 + AB^2. BC là cạnh huyền, AB và AC là 2 cạnh góc vuông, tam giác ABC vuông tại A.

Ứng dụng của việc chứng minh tam giác vuông trong hình học và thực tiễn

Ngoài bộ môn toán học, chứng minh tam giác vuông còn có rất nhiều ứng dụng vào thực tế. Một số ví dụ cụ thể được nêu chi tiết như sau:

• Ngành xây dựng: Nguyên tắc của hình tam giác vuông được sử dụng để thiết kế các phần kiến trúc của công trình, đảm bảo được sự vững chắc và tối ưu không gian.
• Ngành công nghệ: Các tính toán trên tam giác vuông được ứng dụng để tạo ra thuật toán đồ hoạ xử lý hình ảnh, render hình ảnh một cách chính xác và hiệu quả.
• Ngành địa lý: Công thức tính toán các cạnh, các góc tam giác vuông có thể ứng dụng để đo đạc, xác định khoảng cách và ranh giới đất đai.
• Ngành giáo dục: Bài tập chứng minh tam giác vuông giúp học sinh phát triển được các kỹ năng tư duy, từ đó phát triển khả năng làm toán logic.

Xem thêm: Những ứng dụng của trọng tâm tam giác trong thực tiễn

Trên đây là những cách chứng minh hình tam giác vuông đơn giản và hiệu quả nhất. Ôn tập và làm bài tập thường xuyên sẽ giúp các em giải bài tập chính xác và nhanh chóng.