Chu vi hình tam giác là khái niệm quan trọng trong hình học, liên quan đến tổng độ dài của ba cạnh. Việc nắm vững các công thức tính sẽ giúp bạn hiểu rõ hơn về hình học và vận dụng giải các bài tập nâng cao. Cải thiện kiến thức cơ bản về hình học.
Tổng quan về hình tam giác
Tam giác là một hình học phẳng. Trong đó, ba đỉnh của hình không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh lại với nhau. Đây là loại đa giác có số cạnh ít nhất vì chỉ có ba cạnh. Có nhiều loại tam giác khác nhau, dưới đây là khái niệm của một số loại tam giác đặc biệt:
- Tam giác cân có 2 cạnh bằng nhau.
- Tam giác đều có 3 cạnh bằng nhau.
- Tam giác vuông có 1 góc vuông (90 độ).
- Tam giác vuông cân là tam giác vuông với hai cạnh góc vuông bằng nhau. Đây là sự kết hợp của tam giác vuông và tam giác cân, có các tính chất đặc trưng của cả hai loại tam giác này.
Đọc ngay: Tgc là gì? Khái niệm, tính chất và đặc điểm tam giác cân
Công thức tính chu vi hình tam giác chi tiết
Công thức tính chu vi tam giác thường
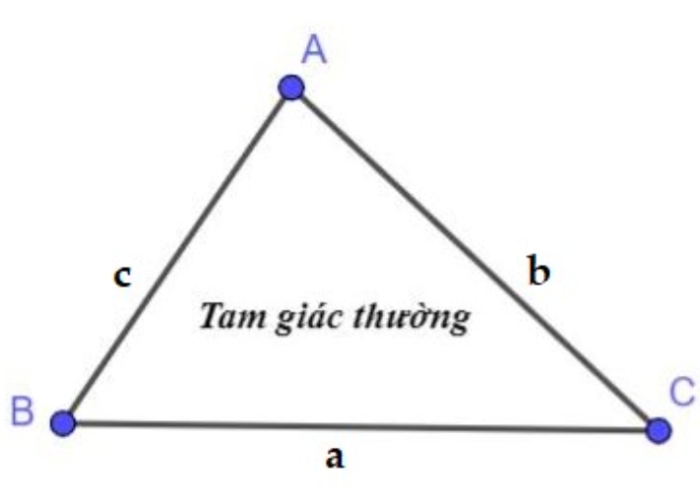
Tam giác thường có ba cạnh không bằng nhau. Để tính chu vi htg, ta chỉ cần cộng tổng độ dài của ba cạnh lại.
Công thức:
$$P\;=\;a\;+\;b\;+\;c$$
Trong đó:
- P: Chu vi của tam giác.
- a, b, c: Độ dài 3 cạnh của tam giác.
Xem thêm: Cách chứng minh hình tam giác vuông chi tiết nhất
Công thức tính chu vi tam giác cân
Tam giác cân có 2 góc ở đáy bằng nhau và 2 cạnh bên bằng nhau.
Công thức:
$$P\;=\;2a\;+\;c$$
Trong đó:
- P: Chu vi của tam giác.
- a: Độ dài 2 cạnh bên của tam giác cân.
- c: Độ dài của cạnh đáy.
Công thức tính chu vi tam giác đều
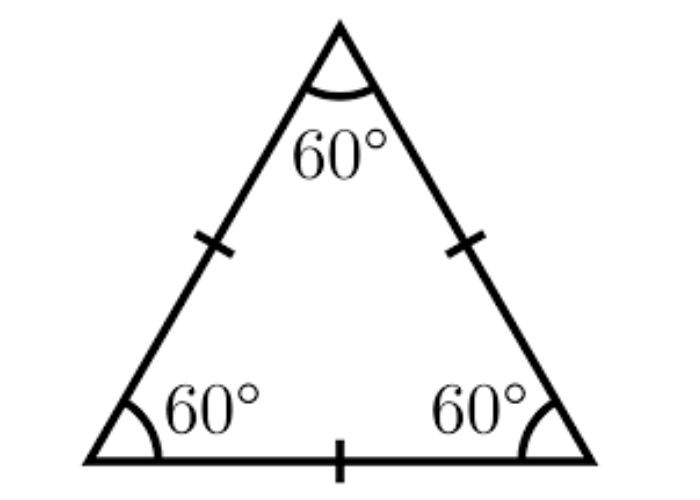
Tam giác đều có 3 cạnh bằng nhau và 3 góc bằng nhau.
Công thức:
$$P\;=\;3\times a$$
Trong đó:
- P: Chu vi của tam giác đều.
- a: Độ dài mỗi cạnh của tam giác đều.
Tham khảo ngay: Hướng dẫn cách chứng minh hình tam giác đều
Công thức tính chu vi tam giác vuông
Tam giác vuông có một góc 90 độ.
Công thức:
$$P\;=\;a\;+\;b\;+\;c$$
Trong đó:
- P: Chu vi của tam giác vuông.
- a, b: Độ dài 2 cạnh góc vuông.
- c: Độ dài cạnh huyền (cạnh đối diện với góc vuông)
Công thức tính chu vi hình tam giác vuông cân
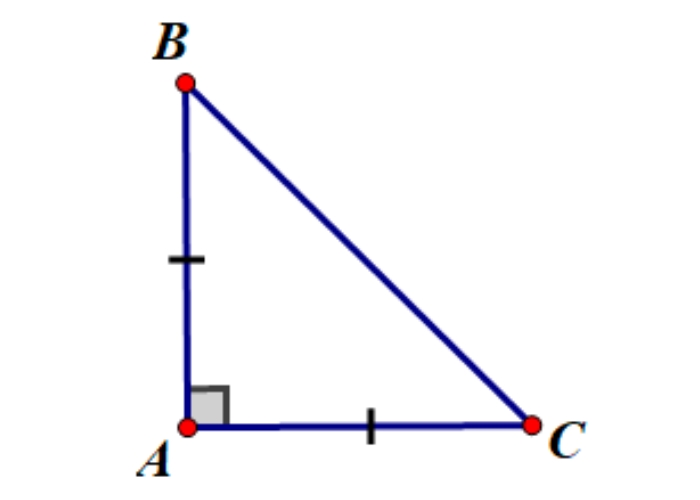
Tam giác vuông cân có một góc 90 độ và hai cạnh góc vuông bằng nhau.
Công thức:
$$P\;=\;2a\;+\;c$$
Trong đó:
- P: Chu vi của tam giác vuông cân
- a: Độ dài hai cạnh góc vuông bằng nhau
- c: Độ dài cạnh huyền
Xem thêm: Đường cao hình tam giác là gì? Công thức tính đơn giản
Một số bài tập ứng dụng tính chu vi htg
Bài 1: Tam giác ABC có các cạnh lần lượt là 3 cm, 5 cm và 7 cm. Chu vi của tam giác ABC là bao nhiêu?
Trả lời:
Áp dụng công thức P = a + b + c:
=> P = 3 + 5 + 7 = 15 cm.
Như vậy, chu vi của tam giác là 15 cm.
Bài 2: Tìm độ dài của cạnh c, nếu P = 30 cm và a = 8 cm, b = 10 cm.
Trả lời:
Áp dụng công thức P = a + b + c:
=> 30 = 8 + 10 + c
=> 30 = 18 + c
Do đó, c = 12 cm.
Bài 3: Tam giác cân có độ dài cạnh đáy là 5 cm và chu vi là 17 cm. Độ dài hai cạnh bên bằng bao nhiêu?
Trả lời:
Đặt độ dài mỗi cạnh bên là a. Áp dụng công thức tính chu vi hình tam giác cân ta có: P = 2a + 5:
=> 17 = 2a + 5
=> 2a = 12
=> a = 6 cm.
Như vậy, độ dài hai cạnh bên là 6 cm.
Bài 4: Tam giác vuông ABC có độ dài hai cạnh góc vuông là 3 cm và 4 cm. Biết cạnh còn lại có độ dài gấp 2 lần tổng hai cạnh tam giác còn lại. Hãy tính chu vi htg ABC.
Trả lời:
Theo đề bài cho, ta có: AB = 3 cm, AC = 4 cm và BC = 2 (AB + AC):
BC = 2 (3 + 4) = 14 cm.
Chu vi tam giác ABC:
=> P(ABC) = AB + AC + BC = 3 + 4 + 14 = 21 cm.
Lời kết
Cập nhật công thức chu vi hình tam giác của các dạng htg là điều cần thiết cho quá trình học tập. Học sinh nên làm các bài tập minh họa nhiều lần để nhớ bài lâu kỹ và đạt kết quả tốt hơn trong thi cử.