Đạo hàm arctan: Công thức, chứng minh và ứng dụng trong toán học

Đạo hàm arctan là một trong những khái niệm quan trọng trong giải tích. Bài viết này sẽ cung cấp công thức đạo hàm arctan, hướng dẫn cách tính và ứng dụng trong các bài toán thực tế. Các bạn sẽ tìm hiểu cách giải bài tập và các mẹo cần thiết để nắm vững kiến thức này.

Đạo hàm arctan là công thức tính đạo hàm của hàm số lượng giác nghịch đảo của hàm số tangent

Đạo hàm arctan là một trong những công thức quan trọng trong phép tính vi phân của hàm số lượng giác nghịch đảo. Công thức này được sử dụng để tính đạo hàm của hàm số arctan(x) và có dạng: (arctan x)’ = 1/(1 + x²).

Việc tính toán đạo hàm của hàm số arctan có ý nghĩa quan trọng trong nhiều ứng dụng thực tế, đặc biệt trong các bài toán về tối ưu hóa và phân tích hàm số. Khi áp dụng công thức này, ta cần lưu ý rằng miền xác định của hàm số arctan là tất cả các số thực, và đồ thị của nó là một đường cong liên tục.

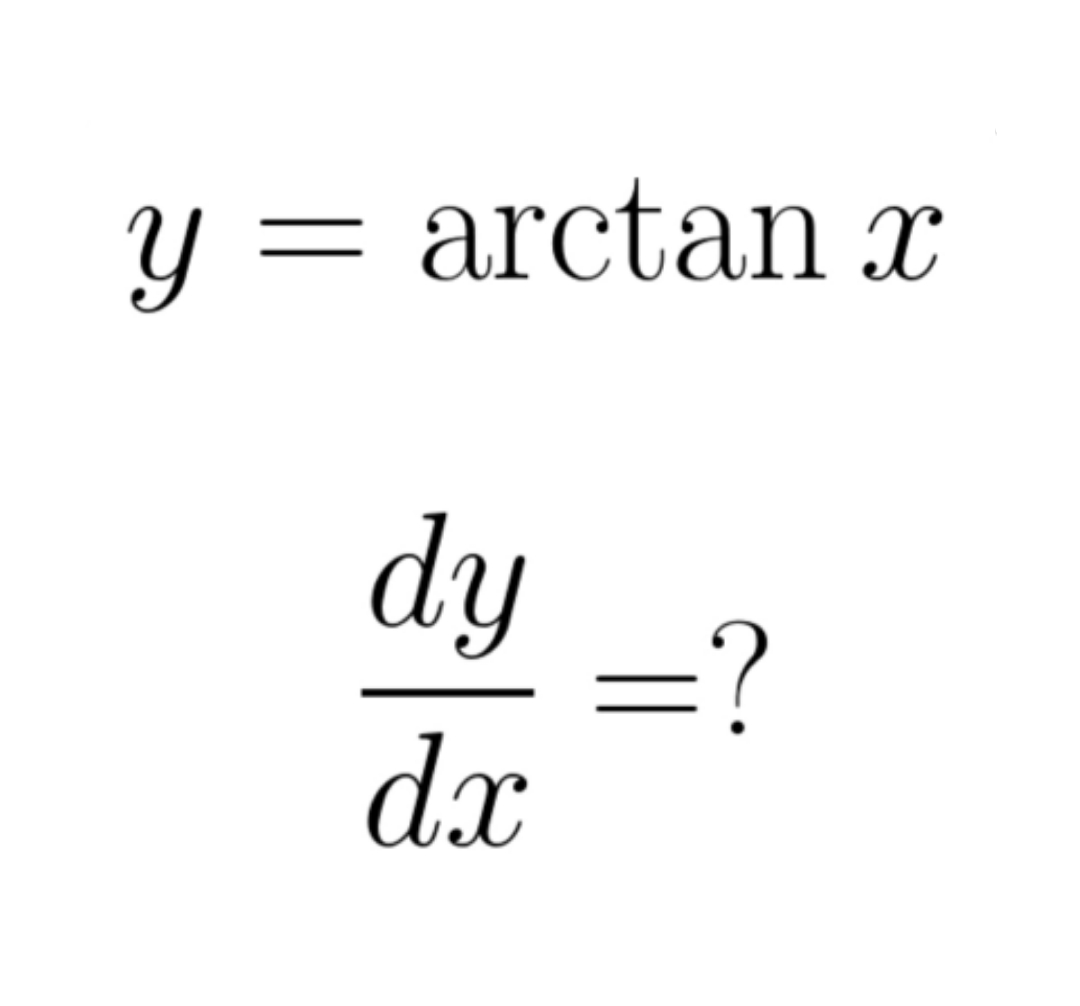
Các arctan function properties cơ bản bao gồm tính chất đối xứng qua gốc tọa độ và giới hạn của hàm số khi x tiến đến vô cực là π/2 và -π/2. Những tính chất này góp phần giúp việc tính toán đạo hàm trở nên dễ dàng và chính xác hơn. Đồng thời, việc nắm vững các tính chất này cũng giúp giải quyết hiệu quả các bài toán phức tạp liên quan đến hàm số arctan.

Công thức đạo hàm arctan cơ bản và cách chứng minh

Đạo hàm arctan là một trong những công thức quan trọng trong giải tích, thường xuyên xuất hiện trong các bài toán phức tạp. Việc nắm vững công thức và cách chứng minh sẽ giúp giải quyết nhiều dạng toán liên quan đến hàm lượng giác ngược.

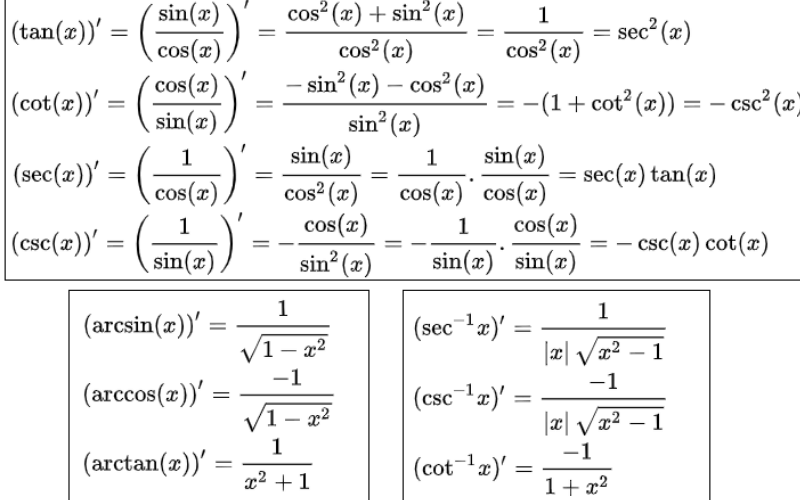
Tương tự như đạo hàm arcsin, đạo hàm của arctan cũng có một công thức cơ bản cần ghi nhớ. Việc hiểu rõ cách chứng minh sẽ giúp áp dụng linh hoạt trong nhiều trường hợp khác nhau.

Công thức đạo hàm arctan x = 1/(1+x²)

Công thức đạo hàm arctan x = 1/(1+x²) là một trong những công thức cơ bản nhất trong phép tính đạo hàm hàm lượng giác ngược. Công thức này áp dụng cho mọi x thuộc tập xác định của hàm arctan.

Khi áp dụng công thức này, cần lưu ý rằng tử số luôn là 1, trong khi mẫu số là biểu thức 1 cộng với bình phương của biến x. Điều này tạo nên một dạng phân thức hữu tỷ đặc biệt.

Chứng minh công thức đạo hàm arctan qua phương pháp đạo hàm hàm ngược

Để chứng minh công thức, ta xuất phát từ định nghĩa hàm ngược. Gọi y = arctan(x), khi đó x = tan(y). Áp dụng phương pháp đạo hàm hàm ngược, ta có:

dy/dx = 1/(dx/dy) = 1/(d(tan y)/dy) = 1/(1 + tan²y) = 1/(1 + x²)

Quá trình chứng minh trên sử dụng các tính chất của hàm lượng giác và đạo hàm hàm ngược. Kết quả cuối cùng cho ta công thức đẹp và gọn gàng.

Ví dụ minh họa tính đạo hàm arctan đơn giản

Xét hàm số f(x) = arctan(2x). Áp dụng quy tắc chuỗi và công thức đạo hàm arctan, ta có:
f'(x) = 1/(1+(2x)²) × 2 = 2/(1+4x²)

Một ví dụ khác với hàm g(x) = arctan(x²):
g'(x) = 1/(1+(x²)²) × 2x = 2x/(1+x⁴)

Các ví dụ trên minh họa cách áp dụng công thức vào các trường hợp cụ thể, từ đơn giản đến phức tạp hơn.

Công thức đạo hàm arctan u và các trường hợp đặc biệt

Đạo hàm arctan u là một trong những công thức quan trọng trong giải tích toán. Công thức này được sử dụng rộng rãi trong việc tính toán các bài toán liên quan đến hàm lượng giác nghịch đảo.

Công thức tổng quát đạo hàm arctan u = u’/(1+u²)

Công thức tổng quát đạo hàm của arctan u được biểu diễn dưới dạng u’/(1+u²), trong đó u’ là đạo hàm của hàm u. Công thức này được chứng minh thông qua phép biến đổi và áp dụng quy tắc lấy đạo hàm hàm hợp.

Khi áp dụng công thức này, cần lưu ý rằng u phải là một hàm số khả vi và miền xác định của hàm arctan u phải thỏa mãn điều kiện 1+u² ≠ 0. Điều này đảm bảo tính chất liên tục và khả vi của hàm.

Các dạng đặc biệt của đạo hàm arctan u

Trong thực tế, công thức đạo hàm arctan u có nhiều dạng đặc biệt tùy thuộc vào dạng của hàm u. Mỗi dạng có những đặc điểm và cách giải quyết riêng.

Đạo hàm arctan của hàm đa thức

Khi u là một hàm đa thức, việc tính đạo hàm trở nên đơn giản hơn. Đầu tiên, ta tính đạo hàm của hàm đa thức u, sau đó thay vào công thức tổng quát.

Ví dụ với u = x², ta có u’ = 2x, do đó đạo hàm arctan(x²) = 2x/(1+x⁴). Tương tự với các hàm đa thức bậc cao hơn.

Đạo hàm arctan của hàm phân thức

Với hàm phân thức, quá trình tính toán phức tạp hơn do cần áp dụng quy tắc đạo hàm thương. Trước tiên, ta tính đạo hàm của tử số và mẫu số riêng biệt.

Sau đó, áp dụng công thức tổng quát và thực hiện các phép biến đổi đại số để đơn giản hóa kết quả cuối cùng. Việc rút gọn biểu thức là bước quan trọng giúp kết quả dễ sử dụng hơn.

Đạo hàm arctan của hàm mũ và logarit

Với hàm mũ và logarit, ta cần kết hợp các quy tắc đạo hàm của hàm mũ và logarit với công thức tổng quát. Điều này đòi hỏi sự thận trọng trong việc xác định miền xác định của hàm.

Đối với hàm mũ như u = e^x, ta có u’ = e^x, nên đạo hàm arctan(e^x) = e^x/(1+e^2x). Với hàm logarit như u = ln(x), ta có u’ = 1/x, do đó đạo hàm arctan(ln(x)) = 1/(x(1+ln²(x))).

Phương pháp giải các bài tập về đạo hàm arctan

Đạo hàm arctan là một trong những dạng toán phổ biến trong chương trình giải tích. Việc nắm vững công thức và phương pháp tính đạo hàm arctan giúp học sinh giải nhanh các bài tập liên quan. Tương tự như định nghĩa lăng trụ, việc hiểu rõ bản chất của hàm arctan sẽ giúp việc tính đạo hàm trở nên dễ dàng hơn.

Các dạng bài tập thường gặp

Trong chương trình toán phổ thông, các bài tập về arctanu đạo hàm thường xuất hiện dưới nhiều dạng khác nhau. Dạng đơn giản nhất là tính đạo hàm của hàm arctan(x) hoặc arctan(ax+b) với a, b là hằng số.

Dạng phức tạp hơn bao gồm tính đạo hàm của tích, thương hoặc hợp của hàm arctan với các hàm số khác. Đặc biệt, nhiều bài tập yêu cầu áp dụng quy tắc chuỗi khi tính đạo hàm của hàm phức hợp có chứa arctan.

Phương pháp giải và mẹo tính nhanh

Để tính how to differentiate arctan hiệu quả, cần nắm vững công thức cơ bản: đạo hàm của arctan(x) là 1/(1+x²). Khi gặp hàm phức tạp, nên chia nhỏ thành các bước giải từng phần.

Một mẹo quan trọng là luôn đặt u = biểu thức bên trong arctan trước khi tính đạo hàm. Điều này giúp tránh sai sót và làm phép tính trở nên rõ ràng hơn. Ngoài ra, việc thành thạo các công thức biến đổi đại số sẽ giúp rút gọn kết quả nhanh chóng.

Bài tập mẫu có lời giải chi tiết

Bài tập 1: Tính y’ nếu y = arctan(2x+1)
Lời giải:

• Đặt u = 2x+1
• Áp dụng công thức: y’ = u’/(1+u²)
• Thay u = 2x+1: y’ = 2/(1+(2x+1)²)
• Kết quả: y’ = 2/(2+4x+4x²)

Bài tập 2: Tính y’ nếu y = x.arctan(x)
Lời giải:

• Áp dụng quy tắc tích: y’ = x.(1/(1+x²)) + arctan(x)
• Rút gọn: y’ = (x/(1+x²)) + arctan(x)

Các bài tập trên minh họa cách vận dụng công thức cơ bản vào các tình huống khác nhau, từ đơn giản đến phức tạp.

Ứng dụng của đạo hàm arctan trong giải tích và thực tế

Đạo hàm arctan có vai trò quan trọng trong việc giải quyết nhiều bài toán giải tích phức tạp. Công thức đạo hàm arctan được ứng dụng rộng rãi trong tính toán cực trị, khảo sát biến thiên và tính giới hạn của các hàm số.

Trong thực tế, đạo hàm arctan thường xuất hiện trong các bài toán về điều khiển tự động, xử lý tín hiệu và thiết kế mạch điện. Ví dụ như trong việc tính toán góc lái của robot tự hành hay điều chỉnh tần số trong các bộ lọc tín hiệu.

Tìm cực trị của hàm số chứa arctan

Việc tìm cực trị của hàm số chứa arctan đòi hỏi áp dụng các kỹ thuật đạo hàm và kiểm tra dấu đạo hàm. Khi xét một hàm số f(x) = arctan(g(x)), ta cần tìm đạo hàm của hàm hợp và xét dấu.

Một ví dụ điển hình là bài toán tối ưu trong công thức thể tích khối lăng trụ, khi cần tìm góc nghiêng tối ưu để đạt thể tích lớn nhất. Phương pháp giải sử dụng đạo hàm arctan giúp tìm ra giá trị chính xác của góc nghiêng cần thiết.

Khảo sát sự biến thiên của hàm số arctan

Khi khảo sát sự biến thiên của hàm số arctan, ta cần xét các yếu tố như tính đơn điệu, điểm uốn và tiệm cận. Hàm arctan có đặc điểm là luôn có hai tiệm cận ngang y = -π/2 và y = π/2.

Trong các arctan applications in calculus, việc phân tích sự biến thiên giúp hiểu rõ hơn về hành vi của hàm số. Điều này đặc biệt quan trọng khi giải quyết các bài toán về tối ưu hóa và mô hình hóa các hiện tượng thực tế.

Tính giới hạn có chứa arctan

Tính giới hạn các biểu thức chứa arctan thường đòi hỏi kết hợp nhiều kỹ thuật tính giới hạn khác nhau. Phương pháp phổ biến là sử dụng các công thức đổi biến và quy tắc L’Hôpital.

Trong quá trình arctan limit evaluation, việc nhận biết các dạng vô định và chọn phương pháp giải phù hợp là yếu tố quyết định. Nhiều bài toán đòi hỏi phải kết hợp với các tính chất đặc biệt của hàm arctan như tính chẵn lẻ hay các công thức cộng.

Khi nghiên cứu về đạo hàm arctan, bạn sẽ khám phá những công thức quan trọng và phương pháp chứng minh thú vị. Bài viết đã trình bày rõ ràng công thức và ứng dụng của đạo hàm arctan trong việc tìm cực trị, khảo sát hàm số và tính giới hạn. Sự hiểu biết về điều này không chỉ giúp cải thiện kỹ năng giải toán mà còn hỗ trợ bạn trong nhiều bài tập thực tế.