Đường kính, bán kính hình tròn là gì? Cách tính và ứng dụng thực tế

Đường kính hình tròn là một dữ liệu rất cần thiết. Khi xác định được đường kính, nhiều công thức tính của hình tròn sẽ được giải đáp như chu vi, diện tích,… Vậy cụ thể đường kính là gì, có cách tính như thế nào? Bạn đọc hãy cùng theo dõi ngay trong bài viết dưới đây để tìm hiểu nhé!

Đường kính hình tròn là gì?

Đường kính hình tròn là một đoạn thẳng đi qua 2 điểm trên hình tròn và tâm của hình tròn đó.

Qua định nghĩa, ta có thể xác định tính chất của đường kính như sau:

• Đường kính là một dây cung đặc biệt của hình khi đi qua tâm.
• Trong tất cả đoạn thẳng đi qua hình thì đường kính là đoạn dài nhất.
• Mỗi hình tròn có vô số đường kính, mỗi đường kính lại chia đôi hình thành 2 nửa bằng nhau.
• Đường kính dài gấp đôi bán kính của hình đó.

Xem thêm: Hình tròn là gì? Đặc điểm của hình tròn

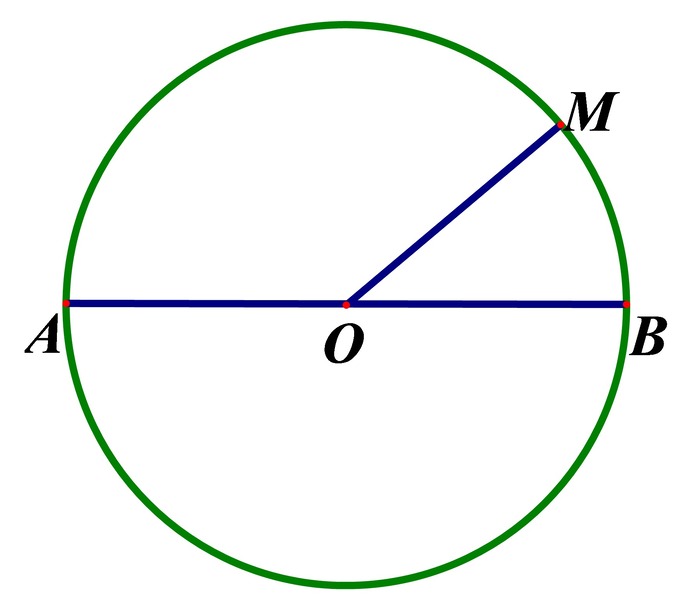
Cách tính đường kính hình tròn

Có rất nhiều cách tính đường kính hình tròn, trong đó bao gồm:

Cách tính đường kính khi biết bán kính

Ta luôn có công thức đường kính dài gấp đôi bán kính. Nếu gọi đường kính là d, bán kính là 2 thì:

d = 2 x r

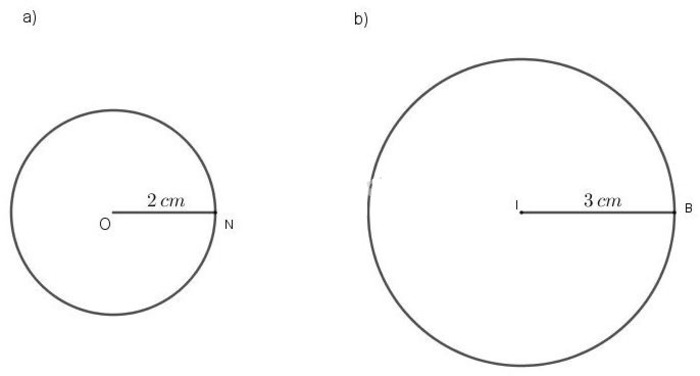
Bài tập ví dụ: Cho hình tròn có bán kính là 2 cm. Vậy đường kính là bao nhiêu?

Lời giải: Đường kính gấp 2 lần bán kính nên đáp án là 2 x 2 = 4cm.

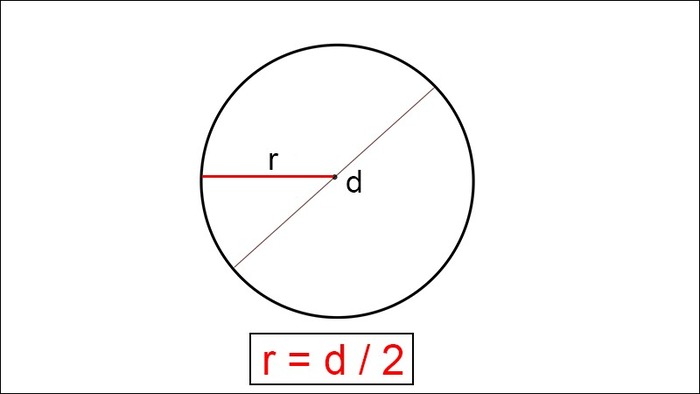
Cách tính đường kính hình tròn khi có chu vi

Công thức tính chu vi hình tròn là

C = 2r x π = d x π.

Suy ra tính đường kính hình tròn có chu vi là:

d = C/π

Số π thường được làm tròn là 3,14.

Bài tập ví dụ: Hình tròn tâm I, biết bán kính là 20cm. Vậy đường kính sẽ là?

Lời giải: Áp dụng công thức sẽ có đường kính d = 20/3,14 = 6,37 cm.

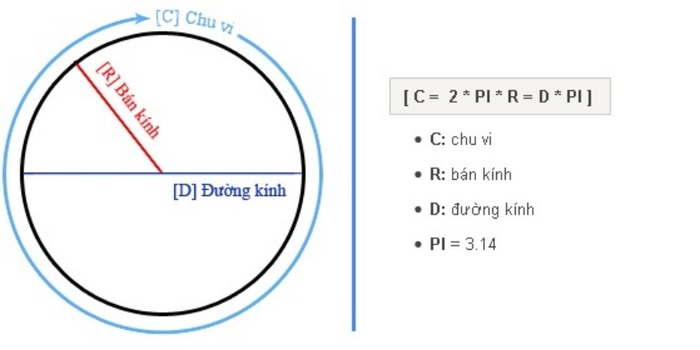
Cách tính đường kính hình tròn khi biết diện tích

Dt hình tròn là

S = π x r2 => r = √(S/π)

Cách tính đường kính hình tròn khi biết diện tích là:

d = 2 x √(S/π)

Bài tập ví dụ: Một hình tròn có diện tích là 50cm2. Như vậy đường kính là

d = 2 x √(50:3,14) = 2 x 3,99 = 7,98 cm.

Một số bài tập thực hành tại nhà

Bài tập 1: Ta có hình tròn với độ dài r là 4cm, hãy tính chiều dài của d.

Bài tập 2: Dùng bộ dụng cụ như compa, thước kẻ vẽ một hình và đo bán kính, đường kính của nó.

Bài tập 3:Tìm ra những sản phẩm có hình ảnh của đường kính trong thực tế.

Bài tập 4: Cho 3 hình tròn, hình 1 có bán kính 5cm, hình 2 có chu vi là 15cm, hình 3 có diện tích là 25 cm2. Tìm đường kính các hình 1, 2, 3.

Bài tập 5: Một hình tròn chu vi là 20dm. Vậy hỏi diện tích của hình là bao nhiêu dm2.

Bài tập 6: Có hai hình tròn với chu vi và diện tích là 15cm và 30 cm2. Đường kính hai hình so với nhau như thế nào?

Lưu ý cần biết khi tính đường kính

Những bài toán về tính đường kính khá đơn giản, nhưng bạn cần lưu ý một số điều sau khi giải:

• Đảm bảo thống nhất đơn vị đo ở các bài tập đã cho.
• Khi tính toán cần chú ý sử dụng kết quả số pi chính xác. Thông thường pi là 3,14 nhưng cũng nhiều trường hợp cần dùng số chính xác hơn là 3,14159.
• Một số trường hợp cần đảm bảo chính xác, cần sử dụng số pi với phần chữ số sau dấu phẩy càng dài càng tốt.
• Đường kính luôn gấp đôi bán kính. Do đó nếu trong tính toán ra kết quả không như vậy, hãy kiểm tra lại kỹ càng.

Xem thêm: Hình tròn có mấy cạnh?

Ứng dụng cách tính đường kính trong thực tế

• Ứng dụng trong khoa học kỹ thuật: Nhiều hệ trục, bánh răng,… của máy móc thiết bị lấy ý tưởng từ hình tròn. Nhờ xác định đường kính mà các chi tiết này sẽ được tạo lập chính xác. Quá trình vận hàng được trơn tru.
• Ứng dụng trong thi công xây dựng: Một số kết cấu của công trình xây dựng ứng dụng hình tròn và đk, bk của hình như cột nhà, ống dẫn, trụ xà,…
• Ứng dụng trong y học: Căn cứ vào đường kính, các bác sĩ có thể xác định được độ rộng của các mạch máu, ống dẫn truyền,… và có phác đồ điều trị bệnh hợp lý nhất.
• Ứng dụng trong nghiên cứu: Từ đường kính sẽ tính được diện tích, thể tích của các đối tượng nghiên cứu,… Khi đó việc nghiên cứu sẽ được thuận lợi, nhanh chóng và dễ dàng hơn.

Bên cạnh đó, rất nhiều ứng dụng khác của đường kính mà bạn có thể bắt gặp dễ dàng trong đời sống hàng ngày.

Bán kính hình tròn là gì?

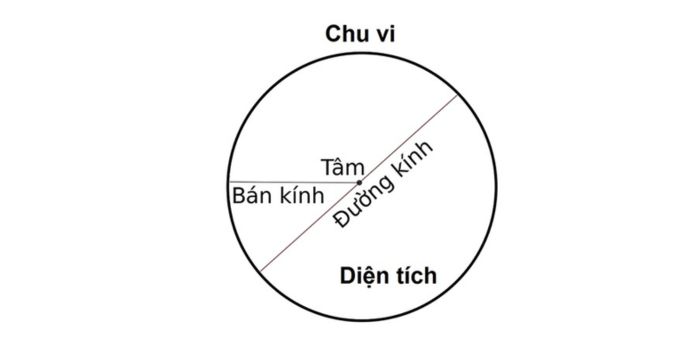
Bán kính hình tròn (bán kính của đường tròn) là khoảng cách tính từ tâm hình tròn đến một điểm bất kỳ trên đường tròn của nó.

Trong toán học, bán kính của hình tròn được ký hiệu bằng chữ “r”.  Giá trị của bán kính là không thay đổi trong một hình tròn. Đây là yếu tố quan trọng trong việc tính toán và xác định các thuộc tính của hình tròn đó.

Xem thêm: Khái niệm ht là gì? Tính chất của hình tròn

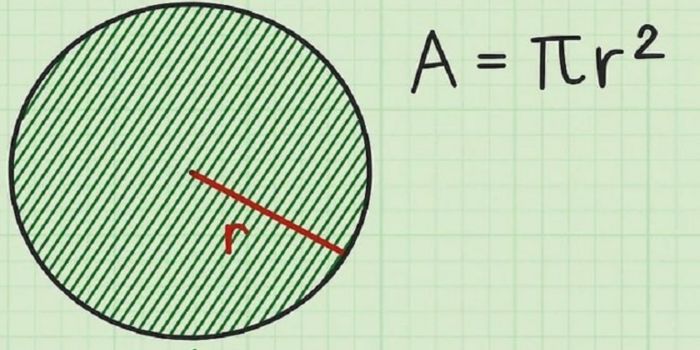
Cách tính bán kính hình tròn

Để tính bán kính của một hình tròn, bạn có thể sử dụng một trong 3 công thức sau đây:

Công thức tính bán kính khi biết đường kính

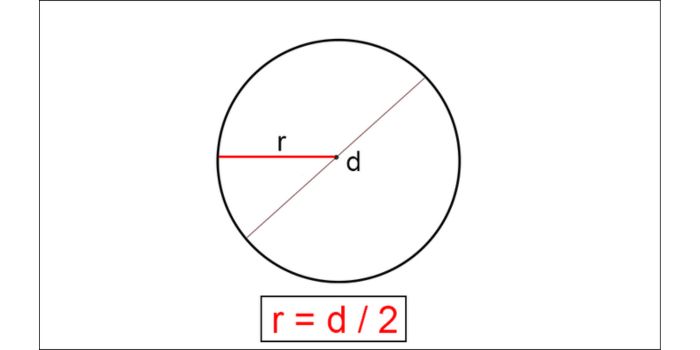
Đường kính hình tròn là độ dài của một đường thẳng đi qua tâm của hình tròn và nối hai điểm trên đường viền của hình tròn. Để tính bán kính từ đường kính, ta có công thức sau:

Trong đó:

• D: Đường kính hình tròn.
• r: Bán kính của hình tròn

Ví dụ: Tính bán kính của một hình tròn có đường kính là 15cm.

Giải: Bán kính (r) = 15 / 2 = 7.5cm

Tìm hiểu thêm: Hình tròn có cạnh không? Đặc điểm của hình tròn

Công thức tính bán kính từ chu vi hình tròn

Chu vi của một hình tròn (C) là độ dài của đường viền hoàn chỉnh của hình tròn đó. Khi biết được chu vi hình tròn, chúng ta có thể xác định được bán hình theo công thức sau:

Trong đó:

• Chu vi (C) là độ dài của đường viền của hình tròn.
• π (pi): hằng số Archimedes có giá trị xấp xỉ 3.14
• r: Bán kính của hình tròn

Ví dụ: Tính bán kính của một hình tròn có chu vi là 15cm

Giải: Bán kính (r) = 15/(2 * 3.14) ≈ 2.38cm

Công thức tính bán kính hình tròn khi biết diện tích

Diện tích của một hình tròn (A) là khu vực bên trong đường viền của hình tròn đó. Khi biết diện tích (A), bạn áp dụng công thức để xác định bán kính như sau:

Trong đó:

• Diện tích (A) là khu vực bên trong của hình tròn
• π (pi): hằng số Archimedes có giá trị xấp xỉ 3.14
• r: Bán kính của hình tròn

Ví dụ: Tính bán kính của một hình tròn có diện tích là 50.24cm

Giải: Bán kính (r) = √(50.24/π (3.14))  = 4cm

Một số bài toán thực hành tại nhà

Để ghi nhớ và thành thạo kiến thức về cách tính bán hình đường tròn, bạn cần thực hành nhiều bài tập liên quan. Dưới đây là một số bài toán gợi ý dành cho bạn:

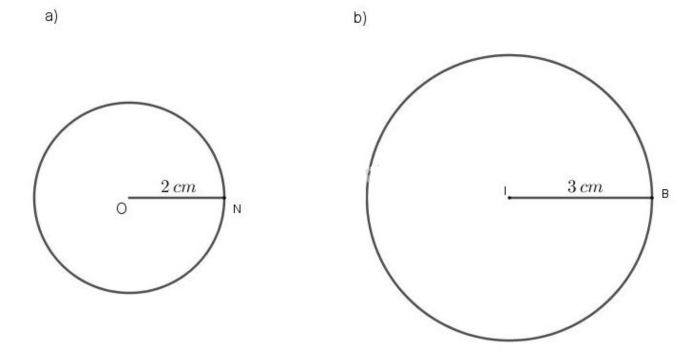
• Bài tập 1: Một hồ nước hình tròn có bán kính là 5m, hãy tính chu vi và diện tích của hồ nước này.
• Bài tập 2: Cho 1 đĩa CD có độ dài đường kính là 12cm. Xác định chu vi và bán kính của CD trên.
• Bài tập 3: Cho biết chu vi của một sân bóng tròn là 66m. Vậy diện tích của sân bóng trên là bao nhiêu?
• Bài tập 4: Một bàn tròn có đường kính 1m. Hãy tính diện tích và chu vi của bàn tròn đó.
• Bài tập 5: Một chiếc bánh pizza hình tròn có chu vi là 20cm. Hãy tính diện tích và bán kính của chiếc bánh trên.

Xem ngay: Công thức tính diện tích hình tròn và bài tập áp dụng

Lưu ý cần biết khi làm bài tập tính bán kính

Tính bán kính hình tròn là bài tập quan trọng khi giải toán hình học. Để đảm bảo áp dụng đúng công thức và ra kết quả chính xác, bạn đừng quên các lưu ý sau:

• Xác định thông tin đã cho: Đọc và hiểu đề bài để xác định thông tin đã cung cấp. Điều này có thể bao gồm đường kính, chu vi, diện tích hoặc các thông tin khác liên quan đến hình tròn.
• Sử dụng công thức chính xác: Dựa vào thông tin đã cho, áp dụng công thức chính xác để tính bán kính. Sử dụng đúng công thức phù hợp với thông tin đã cung cấp (đường kính, chu vi, diện tích).
• Chú ý đơn vị đo: Đảm bảo rằng các đơn vị đo được sử dụng đồng nhất trong bài tập. Bạn nên chuyển đổi đơn vị trước khi tính để đảm bảo tính toán chính xác.
• Làm tròn kết quả: Khi làm tròn kết quả, tuân theo yêu cầu của đề bài hoặc theo quy tắc làm tròn thông thường.
• Kiểm tra lại kết quả: Sau khi tính toán xong, hãy kiểm tra lại kết quả để chắc chắn rằng nó hợp lý và phù hợp với yêu cầu của bài tập.
• Đọc lại đề bài: Trước khi kết thúc, hãy đọc lại đề bài một lần nữa để đảm bảo rằng đã trả lời đúng câu hỏi và đáp ứng đầy đủ yêu cầu của bài tập.

Ứng dụng của bán kính trong thực tế

Bán kính là một khái niệm quan trọng trong hình học và có nhiều ứng dụng thực tế. Dưới đây là một số ví dụ về ứng dụng của bán kính trong cuộc sống hàng ngày:

• Kiến trúc và xây dựng: Bán kính được sử dụng để thiết kế và xác định kích thước của các cấu trúc tròn trong kiến trúc. Chẳng hạn như cột tròn, cầu tròn, hoặc khuôn viên hình tròn của các công trình xây dựng.
• Kỹ thuật đo lường: Bán kính được sử dụng trong các công cụ đo lường để xác định kích thước và độ dài của các vật thể tròn hoặc các đường tròn liên quan.
• Khoa học tự nhiên: Bán kính được sử dụng trong nhiều lĩnh vực của khoa học tự nhiên, chẳng hạn như trong nghiên cứu vật lý, thiên văn học, sinh học,…

Trên đây là bài viết chi tiết về đường kính, bán kính hình tròn. Cùng với đó, những cách tính đơn giản nhất cũng được Học thế nào gửi đến bạn đọc. Hy vọng kiến thức hình tròn này sẽ giúp ích cho bạn trong học tập và ứng dụng hiệu quả ở cuộc sống thường ngày.