Hệ tọa độ cực và công thức chuyển đổi trong toán học dễ hiểu

Hệ tọa độ cực là một công cụ mạnh mẽ để biểu diễn điểm trong mặt phẳng bằng khoảng cách và góc. Phương pháp này không chỉ giúp bạn hình dung rõ hơn về hình học mà còn hỗ trợ giải quyết nhiều bài toán thực tiễn. Khám phá cấu trúc, chuyển đổi và ứng dụng của hệ tọa độ cực để nâng cao kiến thức toán học của bạn ngay hôm nay.

Hệ tọa độ cực là phương pháp biểu diễn điểm trong mặt phẳng bằng khoảng cách và góc

Hệ tọa độ cực là một cách biểu diễn vị trí của điểm trong mặt phẳng thông qua hai thành phần: khoảng cách từ điểm đến một điểm cố định (gọi là cực) và góc tạo bởi đường nối điểm với cực so với một đường thẳng cố định (trục cực). Phương pháp tọa độ hóa này đặc biệt hữu ích khi mô tả các đường cong có dạng xoắn ốc hoặc các chuyển động quay.

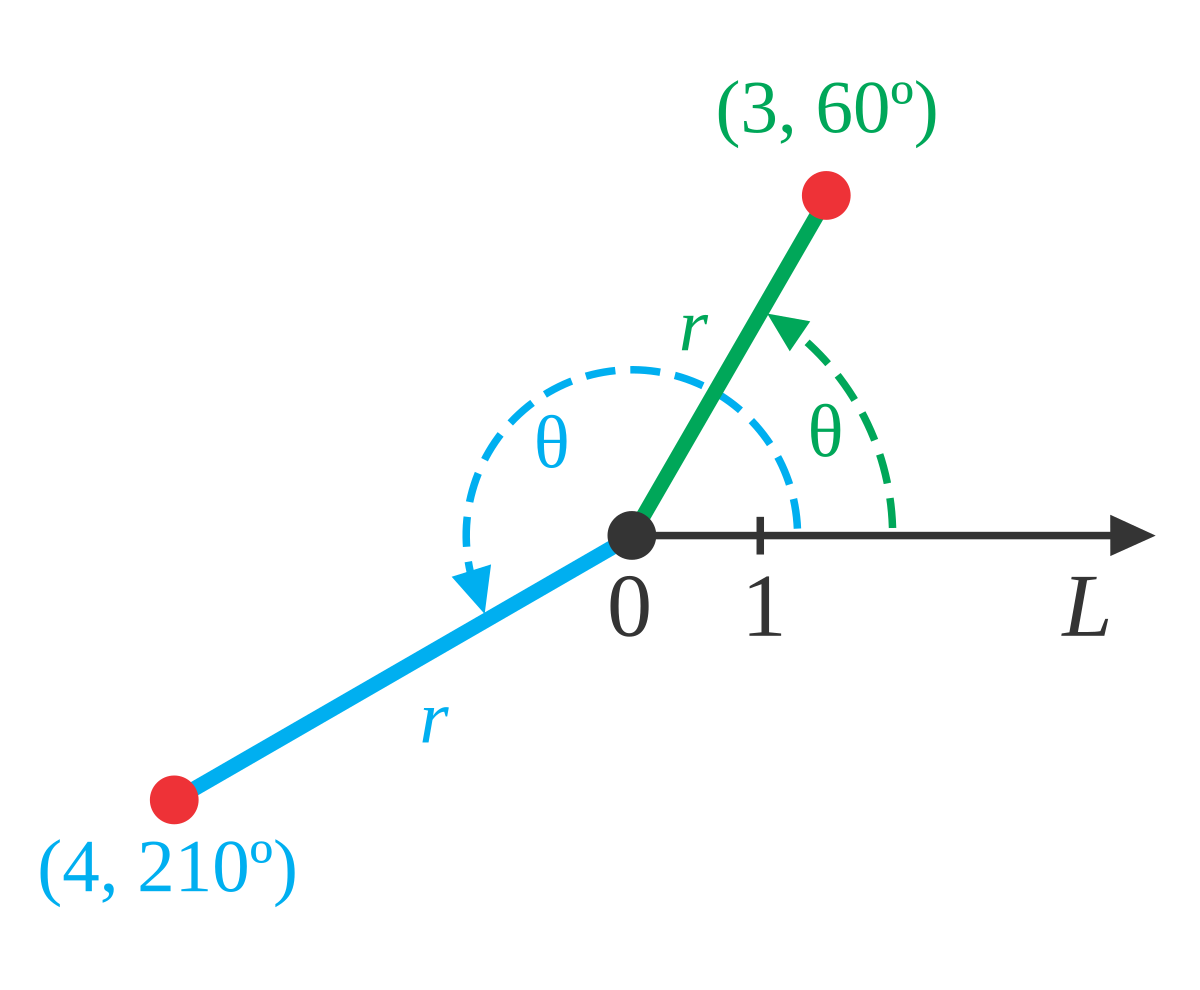
Trong tọa độ cực, mỗi điểm được xác định bằng cặp số (r,θ), trong đó r là khoảng cách từ điểm đến cực O, còn θ là góc tạo bởi đường nối điểm với cực và trục cực. Phương pháp này cho phép biểu diễn các điểm trong mặt phẳng một cách trực quan và tự nhiên hơn so với hệ tọa độ Descartes trong nhiều trường hợp.

Ưu điểm nổi bật của hệ tọa độ này là khả năng mô tả chính xác các chuyển động tròn và các đường cong có tính chu kỳ. Ví dụ, quỹ đạo của các hành tinh quanh mặt trời, chuyển động của các vệ tinh, hay các hiện tượng sóng âm đều được biểu diễn một cách tự nhiên và đơn giản hơn khi sử dụng hệ tọa độ cực.

Các thành phần cơ bản và cách xác định điểm trong hệ tọa độ cực

Hệ tọa độ cực là một hệ tọa độ hai chiều xác định vị trí của điểm trong mặt phẳng thông qua khoảng cách từ điểm đến một điểm cố định và góc tạo bởi đường nối điểm với điểm cố định so với một đường thẳng cố định. Hệ tọa độ này đặc biệt hữu ích khi nghiên cứu các chuyển động tròn và các đường cong có dạng xoắn ốc.

Để xác định chính xác vị trí của một điểm trong hệ tọa độ cực, cần nắm vững các kiến thức về lý thuyết lượng giác và hiểu rõ ba thành phần cơ bản. Ba thành phần này bao gồm cực, trục cực và góc cực, mỗi thành phần đóng vai trò quan trọng trong việc định vị điểm cực.

Cực và trục cực trong hệ tọa độ

Cực là điểm cố định được chọn làm gốc của hệ tọa độ, thường được ký hiệu là O. Đây là điểm quy chiếu để đo khoảng cách đến các điểm khác trong mặt phẳng. Cực đóng vai trò tương tự như gốc tọa độ trong hệ tọa độ Đề-các.

Trục cực là một tia xuất phát từ cực theo một hướng cố định, thường được chọn là hướng ngang sang phải và được ký hiệu là Ox. Trục này có vai trò như trục hoành trong hệ tọa độ Đề-các, tạo cơ sở để đo góc của các điểm trong mặt phẳng.

Khoảng cách từ điểm đến cực (bán kính cực)

Bán kính cực r là khoảng cách từ một điểm bất kỳ trong mặt phẳng đến cực O. Giá trị này luôn không âm và được đo bằng đơn vị độ dài. Khi r = 0, điểm đang xét trùng với cực O.

Việc xác định bán kính cực có thể thực hiện bằng thước đo hoặc tính toán dựa trên công thức khoảng cách giữa hai điểm. Trong nhiều ứng dụng thực tế như radar hay hệ thống định vị, bán kính cực được xác định thông qua các thiết bị đo chuyên dụng.

Góc cực và cách xác định

Góc cực θ là góc tạo bởi trục cực và đường thẳng nối điểm đang xét với cực O. Góc này được đo theo chiều ngược chiều kim đồng hồ, với giá trị từ 0° đến 360° hoặc từ -180° đến 180°.

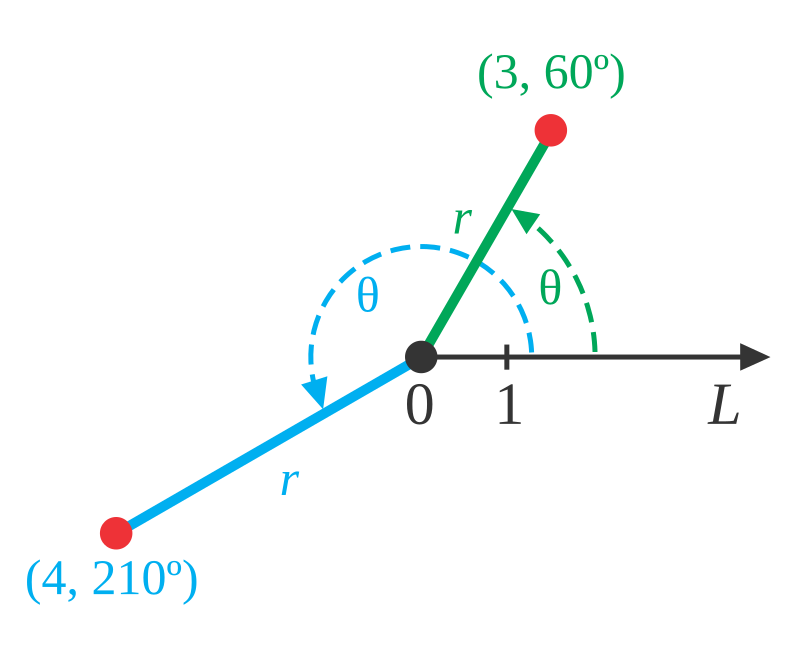
Để xác định góc cực chính xác, có thể sử dụng thước đo góc hoặc tính toán thông qua các hàm lượng giác ngược. Trong thực tế, góc cực thường được biểu diễn theo đơn vị độ hoặc radian tùy thuộc vào yêu cầu cụ thể của bài toán.

Việc xác định góc cực đòi hỏi sự cẩn thận và chính xác, đặc biệt khi làm việc với các ứng dụng kỹ thuật như định vị vệ tinh hay thiết kế các hệ thống quay. Sai số trong việc xác định góc có thể dẫn đến những sai lệch đáng kể trong kết quả cuối cùng.

Chuyển đổi giữa tọa độ Đề-các và tọa độ cực

Việc chuyển đổi tọa độ cực và tọa độ Đề-các là một kỹ năng quan trọng trong toán học và vật lý. Mỗi hệ tọa độ có những ưu điểm riêng phù hợp với từng bài toán cụ thể. Theo Học Thế Nào VN, việc nắm vững cách chuyển đổi giữa hai hệ tọa độ này giúp giải quyết nhiều bài toán phức tạp một cách đơn giản hơn.

Công thức chuyển từ tọa độ cực sang tọa độ Đề-các

Khi chuyển từ tọa độ cực (r,θ) sang tọa độ Đề-các (x,y), ta sử dụng các công thức lượng giác cơ bản. Trong đó r là khoảng cách từ điểm đến gốc tọa độ, θ là góc tạo bởi đường nối điểm với gốc tọa độ và trục hoành.

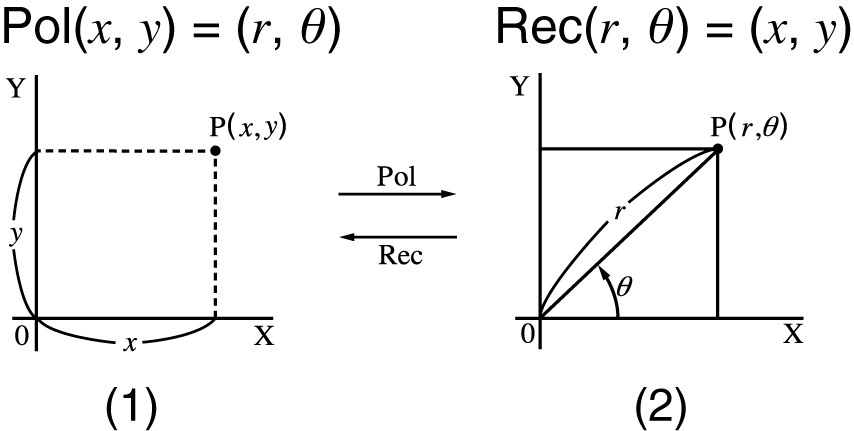
Công thức chuyển đổi được xác định như sau:
x = r.cos(θ)
y = r.sin(θ)

Công thức chuyển từ tọa độ Đề-các sang tọa độ cực

Quá trình chuyển từ tọa độ Đề-các (x,y) sang tọa độ cực và tọa độ đề cần sử dụng định lý Pythagore và các hàm lượng giác ngược. Khoảng cách r được tính bằng căn bậc hai tổng bình phương của x và y.

Công thức chuyển đổi:
r = √(x² + y²)
θ = arctan(y/x)

Lưu ý khi tính θ cần xét dấu của x và y để xác định góc phần tư chính xác.

Ví dụ minh họa việc chuyển đổi tọa độ

Xét điểm A có tọa độ Đề-các là (3,4). Ta có thể chuyển sang tọa độ cực như sau:
r = √(3² + 4²) = 5
θ = arctan(4/3) ≈ 53.13°

Ngược lại, nếu điểm B có tọa độ cực là (5, π/6), ta chuyển sang tọa độ Đề-các:
x = 5.cos(π/6) ≈ 4.33
y = 5.sin(π/6) = 2.5

Biểu diễn các đường cong cơ bản trong hệ tọa độ cực

Việc biểu diễn các đường cong trong hệ tọa độ cực đóng vai trò quan trọng trong toán học và ứng dụng thực tế. Các đường cong này được mô tả thông qua mối quan hệ giữa khoảng cách r từ gốc tọa độ đến một điểm và góc θ tạo bởi đường nối điểm đó với trục cực.

Các đường cong cơ bản trong hệ tọa độ cực bao gồm đường thẳng, đường tròn và các đường xoắn ốc. Mỗi loại đường cong có những đặc điểm và phương trình riêng biệt, giúp mô tả chính xác các hiện tượng trong tự nhiên và kỹ thuật.

Đường thẳng trong hệ tọa độ cực

Đường thẳng trong hệ tọa độ cực được biểu diễn bằng phương trình r = a/cosθ hoặc r = a/sinθ, trong đó a là hằng số. Phương trình này cho thấy mối quan hệ giữa khoảng cách r và góc θ khi điểm di chuyển trên đường thẳng.

Khi đường thẳng đi qua gốc tọa độ, phương trình trở nên đơn giản hơn với dạng θ = α, trong đó α là góc giữa đường thẳng và trục cực. Điều này tạo nên một tia thẳng từ gốc tọa độ.

Đường tròn cực và phương trình

Đường tròn cực có phương trình dạng r = 2a.cosθ hoặc r = 2a.sinθ, với a là bán kính. Phương trình này mô tả một đường tròn tiếp xúc với trục cực tại gốc tọa độ.

Trong trường hợp tổng quát, đường tròn có tâm không trùng với gốc tọa độ có phương trình r² – 2ar.cosθ = b², trong đó a và b là các hằng số xác định vị trí tâm và bán kính của đường tròn. Đây là dạng phổ biến nhất của đường tròn trong hệ tọa độ cực.

Đường xoắn ốc và các đường cong đặc biệt

Các đồ thị trong hệ tọa độ cực có thể tạo ra nhiều đường cong phức tạp và đẹp mắt. Đường xoắn ốc Archimedes có phương trình r = aθ, trong đó a là hằng số xác định tốc độ cuộn của đường xoắn.

Ngoài ra còn có đường xoắn ốc logarit với phương trình r = ae^(bθ), và đường hoa hồng với phương trình r = a.cos(nθ) hoặc r = a.sin(nθ). Những đường cong này thường xuất hiện trong thiên nhiên và được ứng dụng trong nhiều lĩnh vực như kiến trúc, nghệ thuật và khoa học.

Các đường cong đặc biệt này không chỉ có giá trị toán học mà còn mang tính thẩm mỹ cao, tạo nên những hình dạng độc đáo và ấn tượng trong không gian hai chiều.

Ứng dụng của hệ tọa độ cực trong thực tiễn và khoa học kỹ thuật

Hệ tọa độ cực đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghệ. Hệ tọa độ này cho phép biểu diễn vị trí của điểm trong mặt phẳng thông qua khoảng cách từ gốc tọa độ và góc tạo với trục tham chiếu, mang lại nhiều ưu điểm trong việc mô tả các hiện tượng có tính chất quay hoặc tuần hoàn.

Ứng dụng trong vật lý và thiên văn học

Trong vật lý, ứng dụng hệ tọa độ cực giúp mô tả chuyển động của các vật thể theo quỹ đạo tròn hoặc elip một cách trực quan. Các nhà khoa học sử dụng hệ tọa độ này để nghiên cứu chuyển động của các hành tinh quanh Mặt Trời, tuân theo định luật Kepler.

Trong lĩnh vực thiên văn học, các nhà nghiên cứu áp dụng hệ tọa độ cực để xác định vị trí của các thiên thể trên bầu trời. Theo nghiên cứu của Đài thiên văn Greenwich, việc sử dụng hệ tọa độ này giúp tăng độ chính xác trong việc theo dõi quỹ đạo của các vệ tinh nhân tạo.

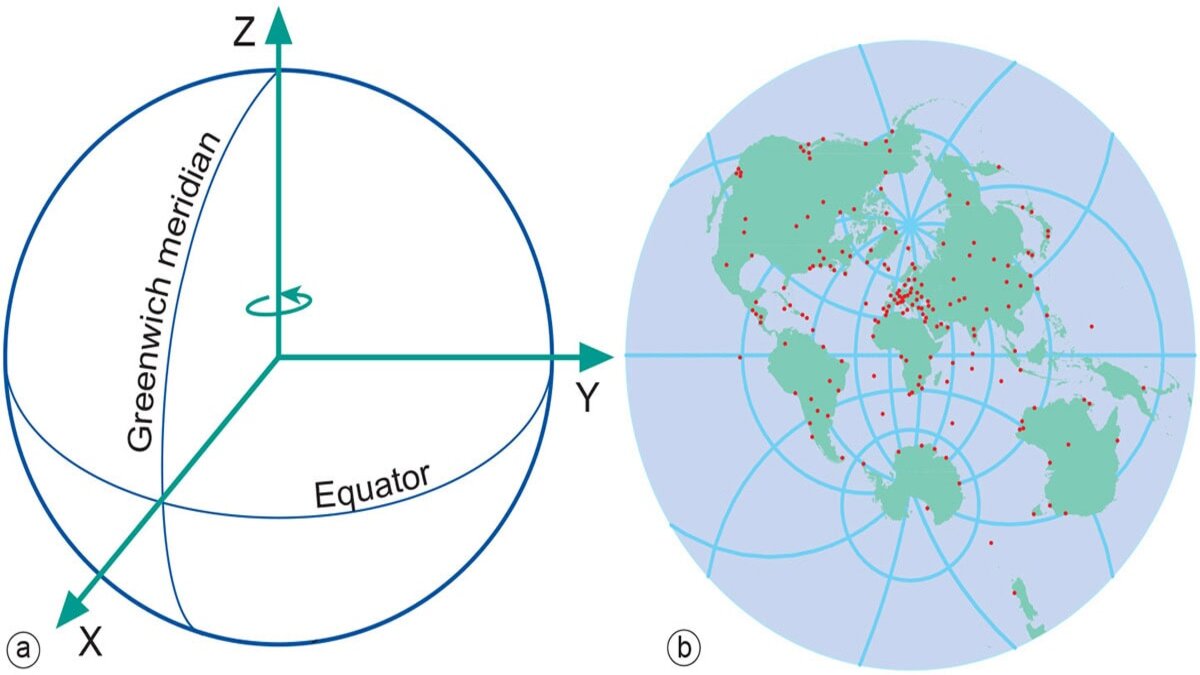
Ứng dụng trong kỹ thuật và công nghệ

Trong lĩnh vực radar và sonar, công thức tọa độ cực được ứng dụng để xác định vị trí của các vật thể. Hệ thống radar quét không gian theo góc quay và đo khoảng cách đến mục tiêu, tạo nên bản đồ vị trí chính xác.

Trong công nghiệp chế tạo, hệ tọa độ cực được sử dụng rộng rãi trong máy CNC và robot công nghiệp. Theo số liệu từ Hiệp hội Robot Công nghiệp Quốc tế (IFR), 60% robot công nghiệp sử dụng hệ tọa độ cực để điều khiển chuyển động của cánh tay robot.

Bài tập thực hành và ví dụ minh họa

Một ví dụ điển hình về ứng dụng hệ tọa độ cực là bài toán xác định vị trí của một con tàu trên biển. Giả sử một con tàu cách hải đăng 5km và tạo với hướng Bắc một góc 30°, ta có thể biểu diễn vị trí của tàu bằng tọa độ cực (5, 30°).

Trong thiết kế đồ họa, các phần mềm như AutoCAD và SolidWorks tích hợp công cụ vẽ theo hệ tọa độ cực. Điều này cho phép người dùng tạo ra các hình dạng phức tạp như hoa văn trang trí, bánh răng hay các chi tiết máy có tính đối xứng quay một cách dễ dàng và chính xác.

Các bài tập thực hành thường tập trung vào việc chuyển đổi giữa tọa độ Descartes và tọa độ cực, cũng như ứng dụng để giải quyết các vấn đề thực tế trong kỹ thuật và khoa học.

Hệ tọa độ cực là một công cụ mạnh mẽ giúp mô tả điểm trong mặt phẳng thông qua khoảng cách và góc. Việc hiểu rõ các thành phần cơ bản, cách chuyển đổi tọa độ, và ứng dụng thực tế sẽ hỗ trợ bạn trong học tập cũng như nghiên cứu. Khám phá và áp dụng hệ tọa độ cực sẽ mở ra cho bạn nhiều cơ hội thú vị trong toán học và các lĩnh vực liên quan.