Hướng dẫn cách tìm hình chiếu vuông góc của điểm lên mặt phẳng chiếu trong không gian

Hình chiếu vuông góc của điểm lên mặt phẳng là một khái niệm quan trọng trong hình học không gian. Việc xác định hình chiếu này giúp giải quyết nhiều bài toán thực tế liên quan đến tọa độ. Nắm vững cách tìm hình chiếu không chỉ củng cố kiến thức mà còn phát triển tư duy logic trong toán học.

Hình chiếu vuông góc của điểm lên mặt phẳng là phép chiếu điểm theo phương vuông góc với mặt phẳng

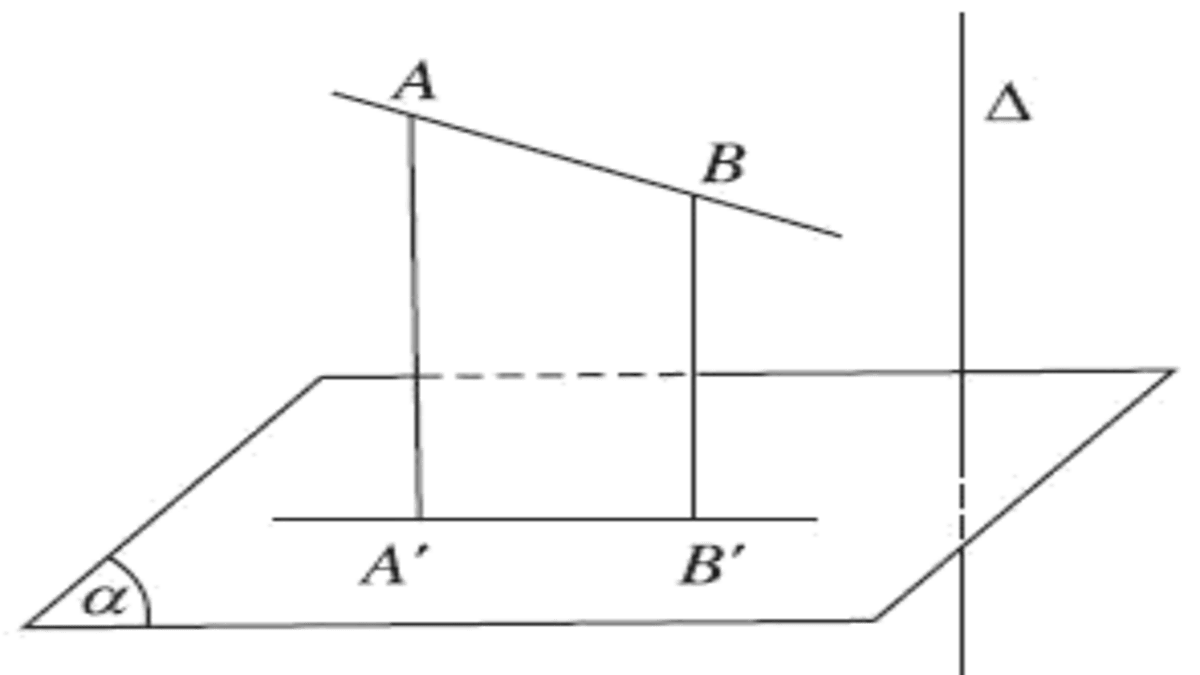
Hình chiếu vuông góc của điểm lên mặt phẳng là phép chiếu điểm theo phương vuông góc với mặt phẳng. Khi thực hiện phép chiếu này, ta kẻ một đường thẳng vuông góc từ điểm cần chiếu đến mặt phẳng chiếu. Giao điểm của đường thẳng này với mặt phẳng chiếu chính là hình chiếu của điểm ban đầu.

Để hiểu rõ hơn về cách xác định hình chiếu vuông góc, hình chiếu là gì toán 7 sẽ giúp bạn nắm được các khái niệm cơ bản. Khi kẻ đường vuông góc từ điểm đến mặt phẳng, đường này sẽ tạo thành góc 90 độ với mặt phẳng chiếu. Đây là điều kiện quan trọng để xác định chính xác vị trí hình chiếu.

Trong thực tế, phép chiếu vuông góc được ứng dụng rộng rãi trong kiến trúc và xây dựng. Ví dụ khi thiết kế nhà, kiến trúc sư cần vẽ các bản vẽ mặt bằng – là hình chiếu vuông góc của công trình xuống mặt phẳng ngang. Điều này giúp thể hiện chính xác kích thước và vị trí các phòng, cũng như mối quan hệ không gian giữa các khu vực trong ngôi nhà.

Các yếu tố cơ bản để xác định hình chiếu vuông góc của điểm lên mặt phẳng

Để xác định chính xác hình chiếu vuông góc của điểm lên mặt phẳng, cần nắm vững 3 yếu tố quan trọng. Việc xác định các yếu tố này giúp quá trình tìm hình chiếu trở nên chính xác và có hệ thống.

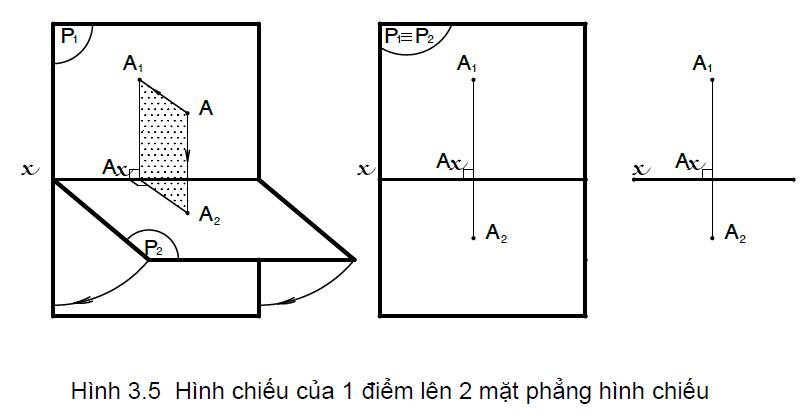
Điểm cần chiếu và tọa độ của điểm trong không gian

Điểm trong không gian cần được xác định bằng tọa độ chính xác theo hệ trục tọa độ Oxyz. Tọa độ này bao gồm 3 thành phần x, y và z tương ứng với vị trí của điểm trên 3 trục tọa độ không gian.

Việc xác định chính xác tọa độ điểm là bước đầu tiên và quan trọng nhất. Sai số trong tọa độ điểm sẽ dẫn đến sai lệch trong kết quả hình chiếu cuối cùng.

Ngoài ra, cần chú ý đến đơn vị đo của các thành phần tọa độ để đảm bảo tính nhất quán trong quá trình tính toán.

Mặt phẳng chiếu và phương trình của nó

Mặt phẳng chiếu được xác định thông qua phương trình tổng quát ax + by + cz + d = 0, trong đó a, b, c là các hệ số xác định vector pháp tuyến của mặt phẳng.

Phương trình mặt phẳng cần được chuẩn hóa để vector pháp tuyến có độ dài bằng 1. Điều này giúp đơn giản hóa các phép tính về sau.

Các hệ số trong phương trình mặt phẳng phải thỏa mãn điều kiện a² + b² + c² ≠ 0 để đảm bảo tính duy nhất của mặt phẳng.

Đường vuông góc từ điểm đến mặt phẳng

Đường vuông góc từ điểm đến mặt phẳng được xác định bởi vector chỉ phương trùng với vector pháp tuyến của mặt phẳng.

Độ dài của đường vuông góc được tính theo công thức:
d = |ax₀ + by₀ + cz₀ + d| / √(a² + b² + c²)
Trong đó (x₀, y₀, z₀) là tọa độ của điểm cần chiếu.

Đường vuông góc này sẽ xác định vị trí của hình chiếu trên mặt phẳng, là yếu tố cuối cùng để hoàn thiện quá trình xác định hình chiếu vuông góc.

Phương pháp tìm hình chiếu vuông góc của điểm lên mặt phẳng

Để tìm hình chiếu vuông góc của một điểm lên mặt phẳng, ta cần thực hiện qua 3 bước chính. Cách tìm hình chiếu của điểm lên mặt phẳng đòi hỏi việc xác định vector pháp tuyến, tính khoảng cách từ điểm đến mặt phẳng và cuối cùng là tìm tọa độ hình chiếu.

Việc tìm hình chiếu của điểm lên mặt phẳng có ý nghĩa quan trọng trong nhiều bài toán hình học không gian, đặc biệt khi ta cần chứng minh hai mặt phẳng vuông góc. Với phương pháp chiếu phù hợp, ta có thể giải quyết bài toán một cách chính xác và hiệu quả.

Xác định vector pháp tuyến của mặt phẳng

Vector pháp tuyến của mặt phẳng là yếu tố then chốt để xác định hướng chiếu vuông góc. Với mặt phẳng có phương trình tổng quát ax + by + cz + d = 0, vector pháp tuyến sẽ có dạng n = (a,b,c).

Để đảm bảo tính chính xác, vector pháp tuyến cần được chuẩn hóa bằng cách chia cho độ dài của nó. Vector đơn vị này sẽ được sử dụng trong các bước tính toán tiếp theo.

Tính khoảng cách từ điểm đến mặt phẳng

Khoảng cách từ một điểm M(x0,y0,z0) đến mặt phẳng ax + by + cz + d = 0 được tính theo công thức:
d = |ax0 + by0 + cz0 + d| / √(a² + b² + c²)

Giá trị khoảng cách này có ý nghĩa quan trọng vì nó chính là độ dài của đoạn thẳng vuông góc từ điểm đến mặt phẳng. Dấu của khoảng cách cho biết điểm nằm về phía nào của mặt phẳng.

Xác định tọa độ hình chiếu

Tọa độ hình chiếu H của điểm M lên mặt phẳng được xác định theo công thức:
H = M – d.n, trong đó:

• M là vector tọa độ điểm cần chiếu
• d là khoảng cách từ điểm đến mặt phẳng
• n là vector pháp tuyến đơn vị của mặt phẳng

Việc tính toán tọa độ hình chiếu cần được thực hiện cẩn thận và kiểm tra lại bằng cách thế tọa độ điểm H vào phương trình mặt phẳng, kết quả phải bằng 0.

Các trường hợp đặc biệt khi tìm hình chiếu vuông góc

Khi xác định hình chiếu của điểm lên mặt phẳng, có một số trường hợp đặc biệt cần lưu ý để tìm kết quả nhanh chóng và chính xác. Việc nắm vững các trường hợp này giúp tiết kiệm thời gian và tránh sai sót trong quá trình giải toán hình học không gian.

Điểm nằm trên mặt phẳng

Khi một điểm nằm trên mặt phẳng, hình chiếu của điểm đó sẽ trùng với chính nó. Điều này xảy ra vì khoảng cách từ điểm đến mặt phẳng bằng 0, không cần phải kẻ đường vuông góc từ điểm xuống mặt phẳng.

Ví dụ, nếu điểm A(2,3,0) nằm trên mặt phẳng Oxy thì hình chiếu của A lên mặt phẳng Oxy chính là điểm A(2,3,0). Đây là trường hợp đơn giản nhất khi tìm hình chiếu.

Điểm nằm trên đường vuông góc với mặt phẳng

Khi điểm nằm trên đường vuông góc với mặt phẳng, hình chiếu của 1 điểm lên mặt phẳng sẽ là giao điểm của đường vuông góc đó với mặt phẳng. Trường hợp này thường gặp khi làm bài toán về khoảng cách từ điểm đến mặt phẳng.

Việc xác định hình chiếu trong trường hợp này khá đơn giản vì đường vuông góc đã được cho sẵn. Ta chỉ cần tìm giao điểm của đường thẳng và mặt phẳng để xác định hình chiếu.

Mặt phẳng song song với các mặt phẳng tọa độ

Khi mặt phẳng song song với một trong ba mặt phẳng tọa độ Oxy, Oyz hoặc Oxz, việc tìm hình chiếu trở nên đơn giản hơn. Ta chỉ cần giữ nguyên hai tọa độ và thay đổi tọa độ còn lại theo phương trình mặt phẳng.

Chẳng hạn, với mặt phẳng P song song với Oxy và có phương trình z = 5, hình chiếu của điểm M(2,3,7) sẽ là điểm M'(2,3,5). Hai tọa độ x và y được giữ nguyên, còn tọa độ z được thay bằng 5 theo phương trình mặt phẳng.

Ứng dụng của hình chiếu vuông góc trong thực tế và bài toán hình học không gian

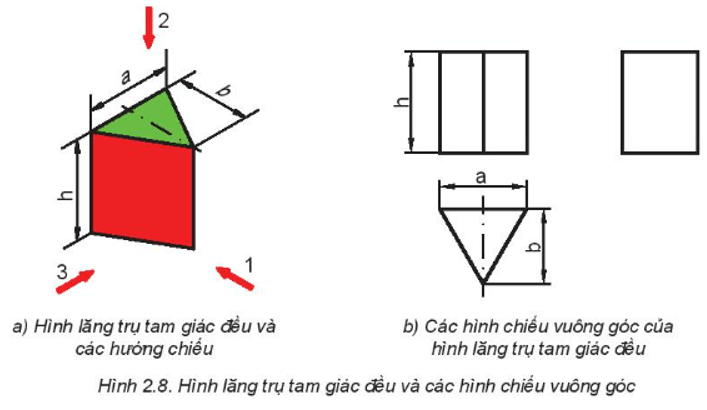
Hình học không gian đóng vai trò quan trọng trong nhiều lĩnh vực thực tiễn, từ kiến trúc đến công nghiệp. Phương pháp hình chiếu vuông góc giúp biểu diễn chính xác các vật thể ba chiều trên mặt phẳng hai chiều, tạo cơ sở cho việc thiết kế và thi công công trình.

Trong lĩnh vực xây dựng, kỹ sư thường sử dụng tọa độ điểm để xác định vị trí chính xác của các cấu kiện. Theo Hocthenao, việc áp dụng hình chiếu không gian giúp tạo ra các bản vẽ kỹ thuật chi tiết, phục vụ quá trình thi công và kiểm tra chất lượng công trình.

Ứng dụng hình chiếu còn xuất hiện trong công nghệ thực tế ảo và mô phỏng 3D. Các chuyên gia tại Autodesk cho biết, kỹ thuật này giúp tạo ra những mô hình số chính xác, phục vụ cho việc thiết kế sản phẩm và quy hoạch đô thị.

Tính khoảng cách từ điểm đến mặt phẳng

Việc xác định khoảng cách từ điểm đến mặt phẳng là một trong những bài toán cơ bản và thiết yếu trong hình học không gian. Phương pháp này được ứng dụng rộng rãi trong ngành xây dựng để tính toán độ cao, khoảng cách an toàn giữa các công trình.

Theo nghiên cứu của Viện Khoa học Công nghệ Xây dựng, việc tính toán chính xác khoảng cách này giúp đảm bảo độ an toàn cho công trình và tối ưu hóa chi phí xây dựng. Kỹ thuật này đặc biệt quan trọng trong thiết kế móng và kết cấu chịu lực.

Xác định góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng và mặt phẳng là yếu tố quan trọng trong thiết kế kiến trúc và xây dựng. Việc xác định chính xác góc này giúp đảm bảo tính thẩm mỹ và độ bền vững của công trình.

Trong thực tế, các kiến trúc sư thường sử dụng phần mềm CAD để tính toán và mô phỏng các góc này. Theo số liệu từ Hiệp hội Kiến trúc sư Việt Nam, việc áp dụng công nghệ số trong tính toán góc giúp giảm 40% thời gian thiết kế và tăng độ chính xác lên đến 98%.

Phương pháp này còn được ứng dụng trong thiết kế cầu thang, mái nhà và các kết cấu nghiêng khác, đảm bảo tính khả thi và an toàn trong quá trình thi công.

Giải các bài toán về hình học không gian

Giải quyết các bài toán hình học không gian đòi hỏi sự kết hợp giữa kiến thức lý thuyết và kỹ năng thực hành. Việc áp dụng các công thức và định lý cần được thực hiện một cách có hệ thống và logic.

Kinh nghiệm từ các chuyên gia giáo dục cho thấy, việc giải bài toán không gian cần tuân theo quy trình: phân tích dữ liệu, vẽ hình minh họa, áp dụng công thức phù hợp và kiểm tra kết quả. Phương phá

Hình chiếu vuông góc của điểm lên mặt phẳng là một khái niệm quan trọng trong hình học không gian. Việc hiểu rõ cách xác định hình chiếu sẽ giúp bạn giải quyết nhiều bài toán liên quan đến tọa độ và khoảng cách. Thông qua các phương pháp đã được trình bày, bạn sẽ dễ dàng áp dụng vào thực tế cũng như phát triển kỹ năng giải toán hiệu quả hơn.