Hình chữ nhật có 2 đường chéo vuông góc là một trong những dạng hình học quen thuộc và quan trọng trong toán học. Tính chất đặc biệt này mang lại nhiều ứng dụng và thuận tiện trong tính toán cũng như giải quyết các vấn đề hình học. Để hiểu rõ hơn về cách giải các dạng bài tập về chủ đề này, mời các bạn cùng theo dõi thông tin chi tiết trong bài viết dưới đây!
Hình chữ nhật có 2 đường chéo vuông góc là hình gì?
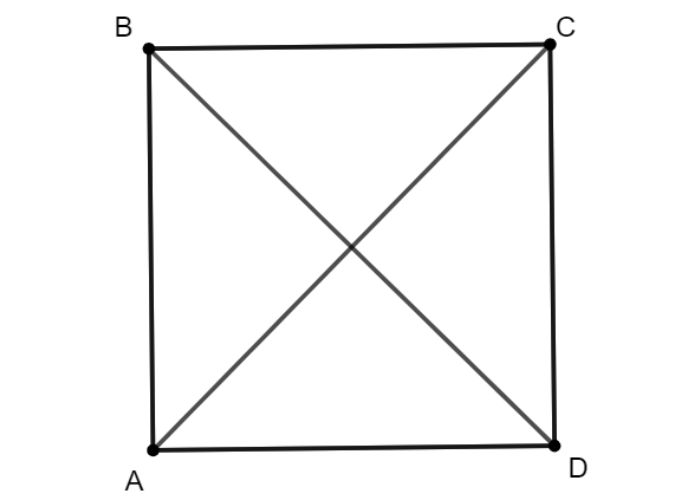
Hình chữ nhật có 2 đường chéo vuông góc là hình vuông. HCN có bốn góc đều là góc vuông và hai cặp cạnh vừa đối diện song song vừa bằng nhau. Đặc biệt, nếu hai đường chéo của hình chữ nhật cắt nhau tạo thành góc vuông, thì hình đó chính là hình vuông.
Như vậy, Học Thế Nào giải đáp cho câu hỏi đang được nhiều bạn quan tâm “Hình chữ nhật có 2 đường chéo vuông góc đúng hay sai?”. Điều này chỉ đúng khi hình chữ nhật là hình vuông, vì trong hình vuông, hai đường chéo mới có thể vuông góc và có cùng độ dài.

Xem thêm: Hcn là gì? Khái niệm, tính chất và đặc điểm nhận biết
Cách chứng minh hình chữ nhật có 2 đường chéo vuông góc
Để chứng minh một hình chữ nhật có hai đường chéo vuông góc với nhau, chúng ta cần thực hiện các bước sau và áp dụng các định lý cơ bản trong hình học:
- Chứng minh hình đó là hình vuông: Trong hình học Euclid, chỉ có hình vuông mới có tính chất hai đường chéo vuông góc với nhau. Do đó, chúng ta cần chứng minh hình chữ nhật đó là hình vuông.
- Áp dụng định lý Pythagoras: Xác định các cạnh của hình chữ nhật và sử dụng định lý Pythagoras để chứng minh rằng tổng bình phương của hai cạnh kề bằng bình phương đường chéo.
- Sử dụng tính chất đường trung bình của tam giác: Nếu tứ giác có trung điểm của mỗi cạnh nối với nhau tạo thành một hình chữ nhật, chứng tỏ hai đường chéo của tứ giác ban đầu cắt nhau tại trung điểm và vuông góc với nhau.
- Kiểm tra tính vuông góc của hai đường chéo: Sử dụng các phương pháp hình học để kiểm tra xem góc tạo bởi hai đường chéo có bằng 90 độ hay không. Cách chứng minh này có thể được thực hiện bằng cách dựng hình và đo đạc hoặc tính toán góc.
Xem ngay: Tổng hợp các dấu hiệu hình chữ nhật chi tiết, đơn giản
Công thức tính đường chéo
Để tính độ dài đường chéo của một hình chữ nhật, bạn có thể sử dụng công thức đơn giản được gọi là định lý Pythagoras. Đây là công thức giúp chúng ta tính được độ dài của đường chéo dựa trên chiều dài và chiều rộng của hình chữ nhật.
Đầu tiên, bạn cần xác định chiều dài, chiều rộng của hình chữ nhật, kí hiệu là a, b.
Tiếp theo, bạn áp dụng công thức:
$$d=a^2+b^2$$
Cuối cùng, thay các giá trị chiều dài, chiều rộng vào công thức và tính toán để tìm ra độ dài của đường chéo.
Tham khảo ngay: Các cách tính diện tích hcn đơn giản, dễ hiểu
Ví dụ các bài toán liên quan
Các bài toán về hình chữ nhật có đường chéo vuông góc thường bao gồm tính toán độ dài đường chéo và chứng minh các tính chất của tứ giác. Dưới đây là một số ví dụ minh họa và cách giải:
Ví dụ 1: Tính độ dài đường chéo của một hình chữ nhật có chiều dài 10dm và chiều rộng 5dm.
Giải
Áp dụng định lý Pythagoras (py-ta-go), công thức tính đường chéo d của HCN là:
d= 102+ 52=125 = 55 dm
Ví dụ 2: Chứng minh rằng tứ giác EFGH là hình chữ nhật khi biết tứ giác ABCD là hình chữ nhật với các đường chéo AB, CD vuông góc tại O, và E, F, G, H là trung điểm của các cạnh AB, BC, CD, và DA tương ứng.
Giải
Tính chất của tứ giác EFGH:
EF, HG là đường trung bình của tam giác ABC, CDA. Vì vậy EF = HG và chúng song song với nhau.
EH, FG là đường trung bình của tam giác BCD, DAB. Nên EH = FG và chúng cũng song song với nhau.
Kết luận:
Vì EF // HG và EH // FG, nên EFGH là một hình bình hành.
Do AB = CD, AB // CD (ABCD là hình chữ nhật), nên EFGH cũng là hình chữ nhật vì có các cạnh đối song song và bằng nhau.
Đọc ngay: Công thức tính chu vi hình chữ nhật dễ hiểu, chính xác
Ứng dụng tính chất toán học vào thực tế
Hình chữ nhật có nhiều ứng dụng thực tế trong cuộc sống nhờ vào các tính chất hình học đặc biệt của nó. Dưới đây là một số ví dụ dễ hiểu:
- Kiến trúc và xây dựng: Hình chữ nhật được sử dụng nhiều trong thiết kế nhà ở, tòa nhà văn phòng và cầu, giúp tối ưu hóa không gian cũng như tạo sự cân đối cho kiến trúc.
- Công nghệ: Nhiều thiết bị điện tử như màn hình máy tính và điện thoại có dạng hình chữ nhật để hiển thị thông tin một cách hiệu quả, dễ sử dụng.
- Thương mại: Trong các cửa hàng, kệ hàng và bàn trưng bày thường có dạng hình chữ nhật để vừa tiết kiệm không gian, vừa dễ dàng sắp xếp sản phẩm một cách khoa học.
- Nông nghiệp: Đất canh tác thường được chia thành các lô hình chữ nhật để dễ quản lý và sử dụng hiệu quả.
- Giáo dục: Hình chữ nhật là một hình cơ bản được dạy trong môn Toán, giúp học sinh hiểu rõ hơn về hình học phẳng.
Những ứng dụng này cho thấy hình chữ nhật không chỉ quan trọng trong toán học mà còn có ích trong nhiều lĩnh vực khác của cuộc sống.

Kết luận và ý nghĩa
Nghiên cứu về hình chữ nhật có hai đường chéo vuông góc tưởng chừng chỉ thuộc về hình học lý thuyết, thế nhưng thực tế lại mang đến nhiều hiểu biết và ứng dụng thực tiễn quan trọng. Dưới đây là một số điểm chính về ý nghĩa của nghiên cứu này:
- Lý thuyết: Hiểu và chứng minh các tính chất của hình chữ nhật có đường chéo vuông góc giúp nâng cao kiến thức hình học, cải thiện khả năng suy luận logic trong toán học.
- Ứng dụng trong thiết kế và công nghệ: Kiến thức này được ứng dụng trong thiết kế kiến trúc, mỹ thuật và các lĩnh vực kỹ thuật khác.
- Giáo dục: Việc học và giảng dạy về hình chữ nhật cũng như các đường chéo vuông góc là phần quan trọng trong chương trình hình học, giúp học sinh hiểu rõ hơn về các tính chất cơ bản của hình học phẳng.
Nghiên cứu về hình chữ nhật có đường chéo vuông góc cũng đóng góp vào sự phát triển của lý thuyết toán học, mở ra những khả năng mới trong việc giải quyết các vấn đề phức tạp hơn trong môn toán cũng như các ngành khoa học khác.
Trên đây là công thức tính cũng như tổng hợp những dạng bài liên quan đến hình chữ nhật có 2 đường chéo vuông góc. Theo dõi thêm các bài viết khác của chúng tôi để cập nhật nhiều kiến thức bổ ích khác!




