Hình thang là gì? Đây là một trong những khái niệm cơ bản của toán học. Với hình dạng đặc biệt, chúng sở hữu các đặc điểm giúp mang lại nhiều giá trị không chỉ trong nghiên cứu học thuật mà còn được ứng dụng rộng rãi ở thực tiễn cuộc sống. Cùng tìm hiểu chi tiết về các đặc điểm, dạng bài tập quan trọng, cũng như ứng dụng thú vị của chúng tại bài viết dưới đây.
Hình thang là gì?
Hình thang là tứ giác lồi có hai cạnh đối song song. Hai cạnh song song gọi là 2 cạnh đáy và 2 cạnh còn lại là các cạnh bên. Trong trường hợp, hình thang có một cạnh bên vuông góc với 2 cạnh đáy thì gọi là hình thang vuông.
Ví dụ minh họa:
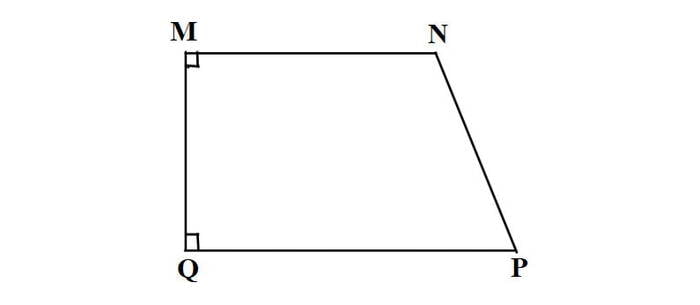
Cho hình thang MNPQ như hình vẽ, ta có:
- MN, PQ là 2 cạnh đáy
- MQ, NP là 2 cạnh bên
- MN//PQ
Trong trường hợp này, MQ vuông góc với MN và QP => hình thang MNPQ là hình thang vuông.
Tính chất của hình thang
Tính chất của hình thang là gì? là phần kiến thức rất quan trọng, các bạn phải chú ý tìm hiểu và trau dồi kiến thức giúp giải nhanh chóng các dạng bài toán về hình này.
Tính chất về góc
- Trong hình thang, Hai góc kề của cạnh bên có tổng số đo là 180 độ.
- Trong hình thang cân, các góc được tạo nên từ cạnh đáy và cạnh bên có số đo bằng nhau.
Tính chất về cạnh
- Nếu một hình thang sở hữu 2 cạnh đáy bằng nhau thì 2 cạnh bên sẽ song song và bằng nhau.
- Nếu hình thang sở hữu 2 cạnh bên song song thì 2 cạnh đáy cũng bằng nhau.
- Hai đường chéo bằng nhau trong hình thang cân.
Tính chất về đường trung bình của hình thang là gì?
- Đường trung bình được định nghĩa là đường thẳng nối hai trung điểm của 2 cạnh bên hình thang.
- Nếu một đường thẳng đi qua trung điểm của 1 cạnh bên và song song với 2 đáy thì tất yếu đi qua trung điểm của cạnh bên còn lại.
- Trong hình thang, đường trung bình sẽ song song với 2 đáy và có độ dài bằng nửa tổng 2 cạnh đáy.
Có thể bạn quan tâm: Dấu hiệu nhận biết hình thang chi tiết nhất.
#4 Hình thang phổ biến hiện nay
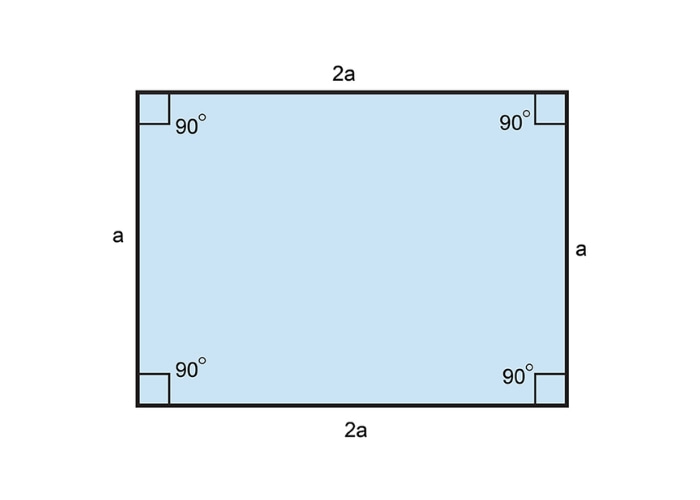
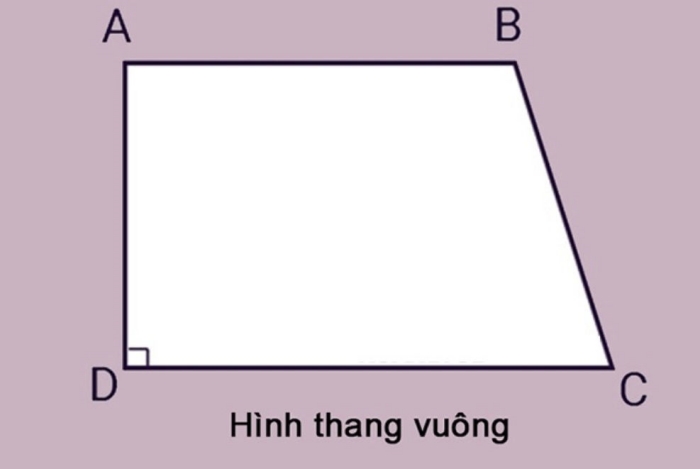
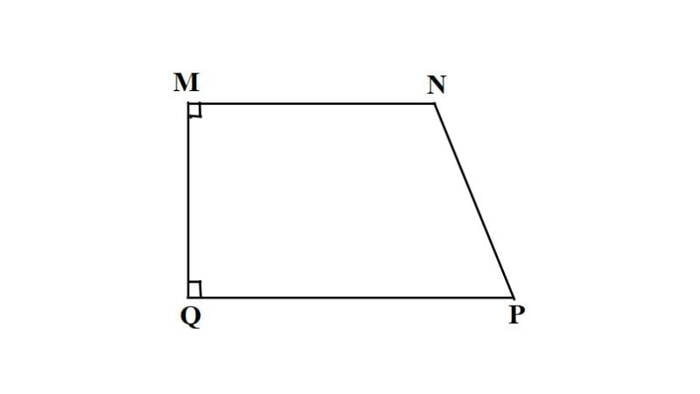
Hình thang có 4 dạng đặc biệt phổ biến gồm: hình thang vuông, hình thang cân, hình bình hành và hình chữ nhật.
- Hình thang vuông: là hình thang có một cạnh bên vuông góc với 2 cạnh đáy. Góc kề cạnh bên này có số đo là 90°.
- Hình thang cân: là hình thang có 2 góc kề một cạnh đáy bằng nhau.
- Hình bình hành: Là hình thang có 2 cạnh đáy bằng nhau, 2 cạnh bên song song và bằng nhau. Các góc đối diện bằng nhau. Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
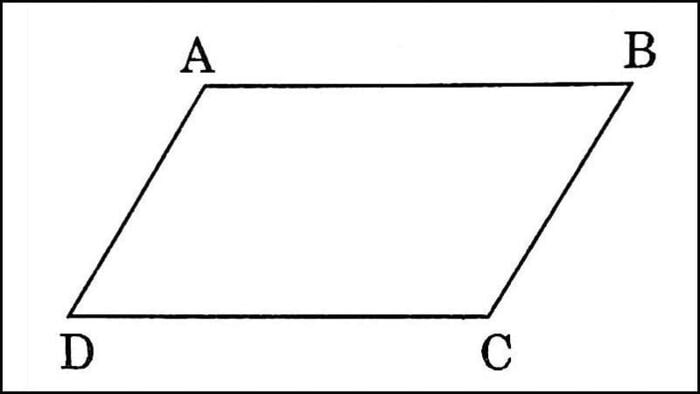
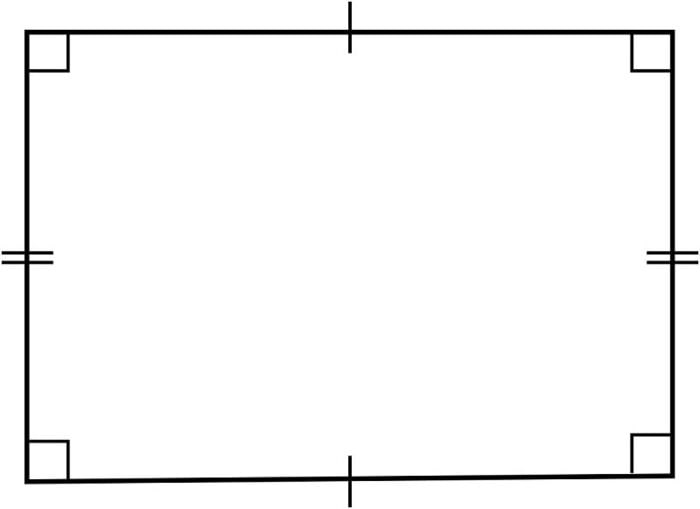
- Hình chữ nhật: Đây là hình bình hành có 4 góc vuông, 2 cạnh đáy bằng nhau và 2 cạnh bên song song và bằng nhau.
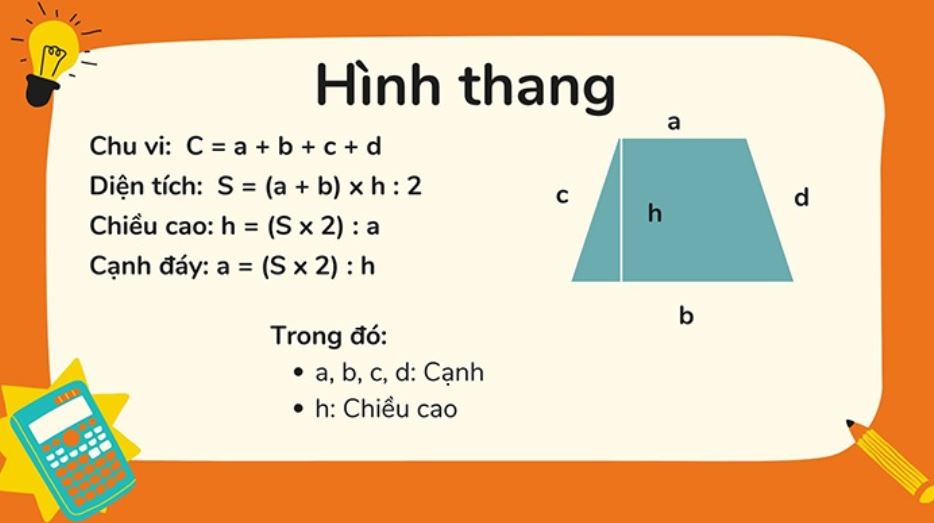
Công thức tính diện tích và chu vi hình thang
Công thức tính diện tích hình thang được tính bằng chiều cao nhân với 1/2 tổng 2 đáy.
S = h x (a + b)/2
Trong đó:
- S: là diện tích hình thang
- h: là chiều cao của hình thang (khoảng cách từ đỉnh vuông góc đến cạnh đáy lớn nhất)
- a và b: là độ dài 2 cạnh đáy của hình thang.
Công thức tính chu vi hình thang được tính bằng tổng của độ dài các cạnh bên và các cạnh đáy.
P = a + b + c + d
Trong đó:
- P: là chu vi của hình thang
- a, b, c, d là độ dài các cạnh của hình thang
Ví dụ minh họa:
Cho hình thang ABCD có AB = 7 cm, CD = 5 cm, AD = 3 cm và BC = 4 cm và chiều cao h là 2 cm. Tính diện tích và chu vi hình thang ABCD.
Hướng dẫn giải:
Áp dụng công thức ta có:
S (ABCD) = 2.(7 + 5)/2 = 12 cm2
P (ABCD) = 7 + 5 + 3 + 4 = 19 cm.
Một số dạng bài tập về hình thang
Dưới đây là một số dạng bài tập về hình thang quan trọng, thường xuất hiện trong các bài kiểm tra.
Dạng 1: Tính số đo góc
Với dạng bài này, các bạn dựa vào các tính chất đặc biệt của hình thang như 2 cạnh đáy song song, tổng số đo của các góc kề 1 cạnh bằng 180 độ. Trong trường hợp, dữ kiện đề bài cho biết hình thang có dạng đặc biệt như hình chữ nhật, hình bình hành, hình thang vuông hoặc hình thang cân thì các bạn có thể sử dụng các đặc điểm, tính chất về cạnh và góc của nó để xử lý bài toán một cách chuẩn xác.
Ví dụ minh họa:
Cho hình thang MNPQ có MN//PQ, góc M = 3 góc Q, góc N – góc P = 30 độ, tính số đo các góc của hình thang.
Hướng dẫn giải:
Theo đề bài ta có, góc M = 3.góc Q mà góc M + góc Q = 180°
=> 3.góc Q + góc Q = 180° ⇔ 4 góc Q = 180° ⇔ góc Q = 45° => góc M = 135°
Tiếp theo, ta có góc N – góc P = 30° ⇔ góc N = 30° + góc P, mà góc N + góc P = 180°
=> 30° + góc P + góc P = 180° ⇔ 2.góc P = 150° ⇔ góc P = 75° => góc N = 105°
Dạng 2. Chứng minh hình thang, hình thang cân, hình thang vuông
Ở dạng này, bạn sử dụng các định nghĩa, tính chất về hình thang vuông, hình thang cân và hình thang để tìm ra hướng chứng minh hình thang.
Ví dụ minh họa:
Cho △MNP cân tại M có ND và PE là hai đường trung tuyến của tam giác. Chứng minh NPDE là hình thang cân.
Dạng 3. Sử dụng các tính chất của hình thang để chứng minh bài toán.
Với dạng này, sử dụng linh hoạt các đặc điểm, tính chất của hình thang để chứng minh bài toán.
Ví dụ minh họa:
Cho hình thang cân MNPQ, ta có MN//PQ và MN < PQ. Gọi X là giao điểm của MQ và NP và I là giao điểm của MP và NQ. Chứng minh:
a) △XMN cân tại X.
b) △MNQ và △NMP bằng nhau.
c) IQ = IP.
Ứng dụng của hình thang trong thực tế
Hình thang là một hình học phổ biến có nhiều ứng dụng trong thực tế, từ kiến trúc đến kỹ thuật và các ngành công nghiệp khác. Dưới đây là một số ứng dụng cụ thể của hình thang.
Kiến trúc và Xây dựng
- Mái nhà: Nhiều mái nhà có hình dạng của một hình thang, đặc biệt là mái dốc. Điều này giúp nước mưa dễ dàng chảy xuống và tránh tình trạng ngập úng.
- Cầu: Một số cầu treo hoặc cầu có cấu trúc dầm sử dụng hình thang để tăng cường sự ổn định và phân bố trọng lượng.
Thiết kế Nội thất và Trang trí
- Bàn và kệ: Một số bàn và kệ có thiết kế chân hình thang để tăng cường sự chắc chắn và thẩm mỹ.
- Đèn: Hình dạng chụp đèn cũng thường là hình thang để ánh sáng được phân bố đều.
Kỹ thuật và Công nghệ
- Cấu trúc đòn bẩy: Trong các máy móc và thiết bị, hình thang có thể được sử dụng trong thiết kế đòn bẩy để đạt được hiệu quả tối đa.
- Ống dẫn khí và chất lỏng: Hình thang có thể được sử dụng trong các thiết kế ống dẫn để điều chỉnh áp suất và lưu lượng.
Giao thông
- Đường và Lề đường: Đường giao thông và lề đường thường có thiết kế hình thang để đảm bảo thoát nước và tránh ngập úng.
- Biển báo giao thông: Một số biển báo giao thông sử dụng hình dạng hình thang để dễ nhận biết và thu hút sự chú ý của người lái xe.
Địa chất và Nông nghiệp
- Kè đá và Bờ kè: Trong các công trình thủy lợi, hình thang được sử dụng để thiết kế kè đá và bờ kè giúp bảo vệ bờ sông, bờ biển khỏi xói mòn.
- Ruộng bậc thang: Ruộng bậc thang trong nông nghiệp có hình dạng hình thang giúp tối ưu hóa diện tích canh tác và giữ nước cho cây trồng.
Qua những chia sẻ trên đây của chúng tôi sẽ giúp các bạn hiểu hơn về định nghĩa hình thang là gì? Các dạng bài tập tiêu biểu và một số ứng dụng thực tế của nó trong cuộc sống. Đừng quên theo dõi bài viết khác của chúng tôi để cập nhật nhiều kiến thức bổ ích nhé!
