Hình vuông là gì? Các ứng dụng thực tế và tính chất của hv như thế nào? Tất cả sẽ được Hocthenao.vn chia sẻ đầy đủ và chi tiết tại bài viết dưới đây, mời các bạn cùng tham khảo.
Hình vuông là gì?
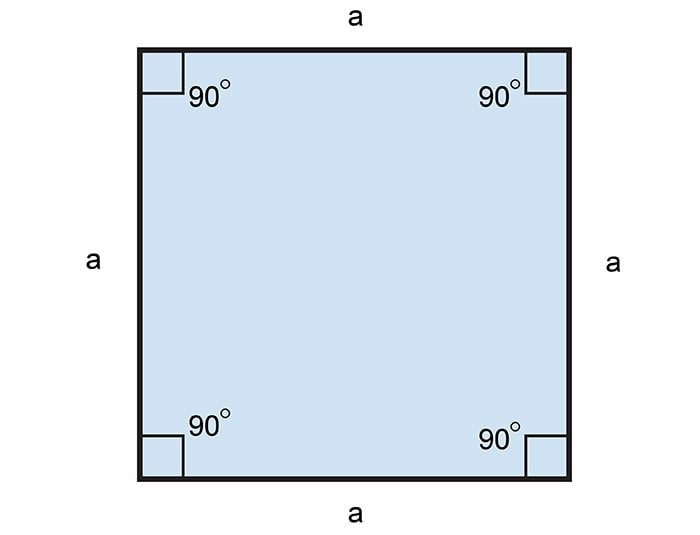
Hình vuông là hình tứ giác đều, chúng có 4 góc bằng nhau (4 góc vuông) và 4 cạnh bằng nhau, được chứng minh trong hình học Euclid.
Ví dụ minh họa:
Từ định nghĩa hình vuông, ta có tứ giác EFGH là hình vuông ⇔ góc E = góc F = góc G = góc H = 90° và EF = FG = GH = HE.
Suy ra tiếp:
- Hình vuông là hình chữ nhật sở hữu 4 cạnh bằng nhau.
- Hình vuông là hình thoi sở hữu 4 góc bằng nhau và bằng 90°.
=> Hình vuông vừa là hình thoi, vừa là hình chữ nhật.
Tính chất của hình vuông
Vì hình vuông vừa là hình chữ nhật, vừa là hình thoi nên hình vuông có đầy đủ tích chất của 2 dạng hình học này, cụ thể như sau:
- Hai đường chéo hình vuông bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
- Hình vuông sở hữu 4 cạnh bằng nhau.
- Một đường chéo chia hình vuông thành 2 phần có diện tích bằng nhau.
- Giao điểm của các đường phân giác, trung trực và trung tuyến đều trùng tại một điểm.
- Hình vuông sở hữu 2 cặp cạnh song song
- Có một đường tròn nội tiếp và ngoại tiếp đồng thời tâm của cả hai đường tròn này trùng nhau, là giao điểm của hai đường chéo của hình vuông.
Dấu hiệu nhận biết hình vuông
Chúng ta có thể nhận biết hình vuông thông qua điểm đặc biệt nào đó của hình chữ nhật và hình thoi, cụ thể như sau:
- Nếu một hình chữ nhật sở hữu 2 cạnh kề bằng nhau thì là hình vuông.
- Nếu một hình chữ nhật có 1 đường chéo là đường phân giác của một góc thì là hình vuông
- Nếu một hình chữ nhật sở hữu 2 đường chéo vuông góc với nhau thì là hình vuông
- Nếu một hình thoi có 2 đường chéo có số đo bằng nhau thì là hình vuông
- Nếu một hình thoi sở hữu 1 góc vuông thì là hình vuông.
Dấu hiệu nhận biết này sẽ giúp các em trong các dạng bài toán chứng minh một hình chữ nhật hoặc hình thoi là hình vuông một cách nhanh chóng.
Công thức tính diện tích và chu vi hv
Chu vi hình vuông được tính bằng tổng 4 cạnh của hình vuông đó hoặc là 4 lần của một cạnh hình vuông (do hình vuông có tính chất 4 cạnh bằng nhau).
Công thức tính chu vi hình vuông:
P = a x 4
Trong đó:
P: là chu vi của hình vuông
a: là độ dài 1 cạnh bất kỳ của hình vuông
Ví dụ minh họa:
Cho một hình vuông có 1 cạnh là 5 cm. Tính chu vi hình vuông đó?
Hướng dẫn giải:
P = 5 x 4 = 20 cm.
Diện tích hình vuông được tính bằng bình phương độ dài một cạnh bất kỳ của hình vuông.
Công thức tính diện tích hình vuông:
$$S=a\times a=a^2$$
Trong đó:
S: là diện tích hình vuông
a: là độ dài một cạnh bất kỳ của hình vuông.
Ví dụ minh họa:
Tính diện tích một hình vuông khi biết độ dài một cạnh của hình vuông đó là 3 cm.
Hướng dẫn giải:
Diện tích hình vuông là: S = 3 x 3 = 9 cm^2
Các phương pháp chứng minh tứ giác là hình vuông
Để chứng minh một tứ giác là hình vuông, các bạn có thể dựa vào các tính chất đặc biệt của hình vuông và dấu hiệu đặc trưng của nó. Dưới đây là một số phương pháp được sử dụng phổ biến trong các bài toán chứng minh hv:
- Chúng ta chứng minh tứ giác đó là hình chữ nhật và kèm theo các đặc điểm như hai cạnh kề bằng nhau hoặc một đường chéo là đường phân giác của một góc hay hai đường chéo vuông góc. Cách chứng minh này thường được áp dụng với tứ giác có 4 góc vuông.
- Chúng ta chứng minh tứ giác đó là hình thoi và sở hữu một trong những đặc điểm đặc biệt như có thêm một góc vuông hoặc hai đường chéo bằng nhau. Phương pháp này được áp dụng khi ta biết tứ giác này có 4 cạnh bằng nhau hoặc đối xứng qua các đường chéo.
Cả hai phương pháp đều yêu cầu bạn vận dụng các tính chất hình học đã biết, cùng với việc quan sát và phân tích kỹ lưỡng hình vẽ nếu có. Để nắm vững và sử dụng thành thạo, bạn nên thực hành với nhiều dạng bài tập đa dạng.
Một số dạng bài tập về hình vuông
Dưới đây là một số dạng bài tập điển hình thường được đưa ra trong các bài kiểm tra về hình vuông:
Dạng 1: Chứng minh hình vuông
Ở dạng bài này, chúng ta có 2 hướng giải quyết như sau:
Cách 1: Chúng ta chứng minh tứ giác đó là hình chữ nhật và kèm theo các đặc điểm như hai cạnh kề bằng nhau hoặc một đường chéo là đường phân giác của một góc hay hai đường chéo vuông góc. Cách chứng minh này thường được áp dụng với tứ giác có 4 góc vuông.
Cách 2: Chúng ta chứng minh tứ giác đó là hình thoi và sở hữu một trong những đặc điểm đặc biệt như có thêm một góc vuông hoặc hai đường chéo bằng nhau. Phương pháp này được áp dụng khi ta biết tứ giác này có 4 cạnh bằng nhau hoặc đối xứng qua các đường chéo.
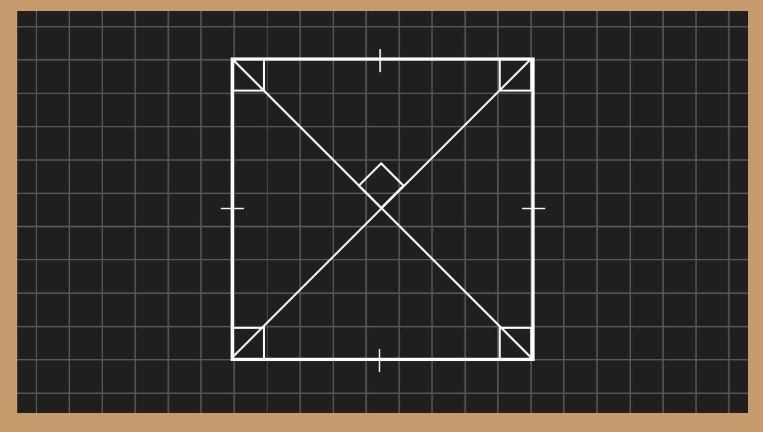
Bài toán minh họa: Cho hình cụ thể bên dưới, dựa vào số liệu cho biết tứ giác AEDF là dạng hình học gì? Giải thích tại sao đưa ra kết luận đó?
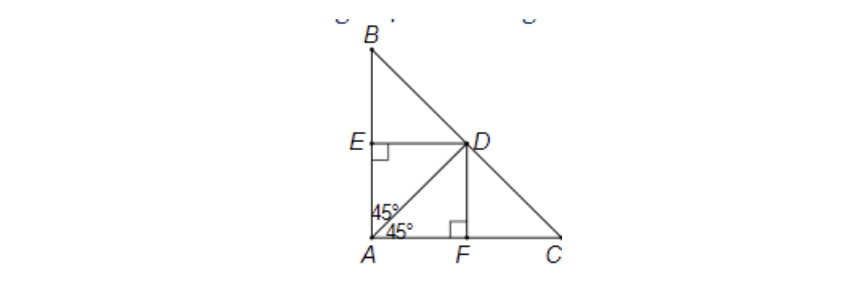
Hướng dẫn giải:
Tứ giác AEDF là hình vuông, vì như sau:
Dựa vào hình vẽ ta có, góc A = góc F = góc E = 90°
Tứ giác có ba góc vuông là hình chữ nhật (dấu hiệu nhận biết)
Ta xét hình chữ nhật AEDF, có AD là đường phân giác của góc A vì góc EAD = góc DAF = 45°.
Nên suy ra: AEDF là hình vuông (dấu hiệu nhận biết).
Dạng 2: Sử dụng định nghĩa, tính chất của hình vuông để chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng
Ở dạng này, các bạn có thể sử dụng linh hoạt định nghĩa, tích chất của hv để chứng minh yêu cầu của đề bài.
Bài tập minh họa: Cho hình vuông có cạnh dài 1m. Vẽ hình vuông thứ hai nhận đường chéo của hình vuông đã cho làm cạnh. Tính độ dài đường chéo của hình vuông này.
Hướng dẫn giải:
Ta xét hình vuông ABCD có cạnh BC = AB = 1m
Tiếp theo, vẽ hình vuông thứ 2 nhận đường chéo AC làm cạnh.
Trên tia đối của tia BA lấy điểm E, tia đối của tia BC lấy điểm F sao cho BE = BF = 1m.
Suy ra: tứ giác AFEC có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình vuông cạnh AC.
=> Đường chéo của hình vuông cần tính là AE = 2m.
Dạng 3: Tìm điều kiện để một hình trở thành hình vuông
Phương pháp giải:
- Áp dụng các dấu hiệu nhận biết hình vuông.
- Nếu bài toán yêu cầu xác định vị trí của một điểm để hình thành hình vuông, ta tiến hành như sau: Giả sử hình đã là hình vuông, sau đó dựa vào các tính chất của hình vuông để xác định vị trí điểm cần tìm.
Bài toán minh họa: Cho tam giác EFH, G là điểm nằm giữa F và H. Qua G kẻ các đường thẳng song song với EF và EH, chúng cắt các cạnh EH và EF theo thứ tự ở A và B.
Ứng dụng các tính chất của hình vuông trong thực tế
Hình vuông không chỉ là dạng hình học quan trọng trong toán học mà còn có rất nhiều ứng dụng thực tế như sau:
- Hình vuông được ứng dụng trong mảng thiết kế và kiến trúc như thiết kế mô-đun và các thành phần của cấu trúc khác để đảm bảo độ chuẩn xác và vẻ đẹp của sản phẩm.
- Trong nghệ thuật, hình vuông là một hình thức cơ bản xuất hiện trong nhiều tác phẩm điêu khắc và hội họa, góp phần tạo nên sự cân bằng và hài hòa cho bố cục.
Trên đây là những chia sẻ của chúng tôi giúp các bạn hiểu rõ về hình vuông là gì? Các ứng dụng và bài tập thường xuất hiện trong đề thi của hv. Đừng quên theo dõi bài viết khác của chúng tôi để cập nhật nhiều kiến thức bổ ích khác nhé!
