Ma trận kề là một công cụ toán học quan trọng được sử dụng để biểu diễn các mối quan hệ giữa các đỉnh trong đồ thị vô hướng. Nó cung cấp một cách thức trực quan và hiệu quả để lưu trữ thông tin về cấu trúc của đồ thị.
Ma trận kề là gì?
Ma trận kề là một công cụ quan trọng trong lý thuyết đồ thị, dùng để biểu diễn cấu trúc của đồ thị dưới dạng ma trận. Đối với một đồ thị có n đỉnh, ma trận kề là một ma trận vuông A kích thước n x n, trong đó mỗi phần tử a[i][j] thể hiện mối quan hệ giữa đỉnh i và đỉnh j.
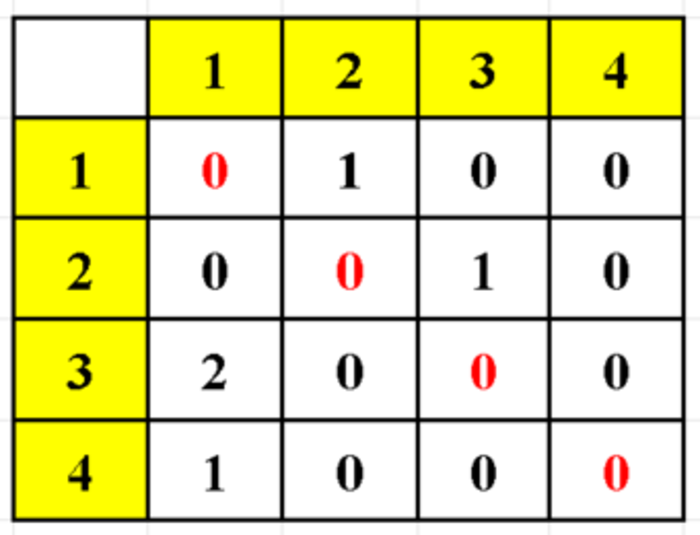
Trong đồ thị vô hướng, a[i][j] bằng 1 nếu có cạnh nối giữa i và j, và bằng 0 nếu không có. Đối với đồ thị có hướng, a[i][j] bằng 1 nếu có cung từ i đến j, và bằng 0 nếu không có. Trong trường hợp đồ thị có trọng số, a[i][j] sẽ là trọng số của cạnh (hoặc cung) nối i và j, nếu có.
Ma trận kề của đồ thị vô hướng luôn đối xứng, và tổng các phần tử trên mỗi hàng (hoặc cột) bằng bậc của đỉnh tương ứng. Công cụ này rất hữu ích trong việc lưu trữ, phân tích và xử lý thông tin về cấu trúc đồ thị, đặc biệt trong các thuật toán đồ thị và ứng dụng thực tế như mạng xã hội, lập kế hoạch đường đi, và nhiều lĩnh vực khác.
Các tính chất của ma trận kề
Dưới đây là những tính chất quan trọng của ma trận kề:
Tính đối xứng
Đối với đồ thị vô hướng, ma trận này luôn là ma trận đối xứng. Điều này có nghĩa là với mọi phần tử a[i][j], ta luôn có a[i][j] = a[j][i]. Tính chất này phản ánh bản chất không định hướng của các cạnh trong đồ thị vô hướng, trong đó một cạnh nối hai đỉnh theo cả hai chiều.
Tổng hàng và cột
Trong ma trận của đồ thị vô hướng, tổng các phần tử trên mỗi hàng (hoặc cột) bằng bậc của đỉnh tương ứng. Điều này cung cấp một cách nhanh chóng để xác định bậc của mỗi đỉnh trong đồ thị mà không cần duyệt qua toàn bộ cấu trúc đồ thị.
Đường chéo chính
Thông thường, các phần tử trên đường chéo chính của ma trận (a[i][i]) có giá trị bằng 0. Tuy nhiên, nếu đồ thị có khuyên (cạnh nối một đỉnh với chính nó), các phần tử tương ứng trên đường chéo chính sẽ có giá trị khác 0, thường là 1 hoặc trọng số của khuyên.
Tính liên thông
Dạng ma trận này có thể được sử dụng để xác định tính liên thông của đồ thị. Nếu tồn tại một lũy thừa k của ma trận kề (A^k) mà tất cả các phần tử đều dương, thì đồ thị là liên thông. Điều này dựa trên việc A^k[i][j] > 0 nếu và chỉ nếu tồn tại đường đi độ dài k từ đỉnh i đến đỉnh j.
Biểu diễn đường đi: Ma trận này cũng cho phép xác định số lượng đường đi giữa các đỉnh. Cụ thể, phần tử thứ [i][j] của A^k (A lũy thừa k) cho biết số lượng đường đi độ dài k từ đỉnh i đến đỉnh j trong đồ thị.
Biểu diễn đồ thị bằng ma trận kề
Cách biểu diễn đồ thị bằng ma trận kề là một phương pháp hiệu quả để mô tả cấu trúc của đồ thị dưới dạng ma trận. Quy trình này bao gồm các bước sau:
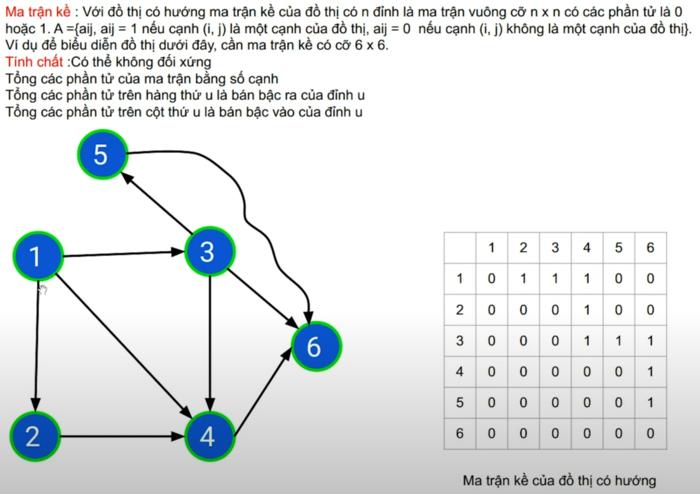
- Bước 1: Đánh số các đỉnh của đồ thị. Gán cho mỗi đỉnh một số nguyên duy nhất từ 1 đến n, với n là tổng số đỉnh của đồ thị.
- Bước 2: Tạo một ma trận vuông A kích thước n x n, trong đó n là số đỉnh của đồ thị. Ban đầu, tất cả các phần tử của ma trận được khởi tạo bằng 0.
- Bước 3: Duyệt qua từng cạnh của đồ thị và cập nhật ma trận như sau:
- Đối với đồ thị vô hướng: Nếu có cạnh nối đỉnh i và j, đặt a[i][j] = a[j][i] = 1.
- Đối với đồ thị có hướng: Nếu có cung từ đỉnh i đến j, đặt a[i][j] = 1.
- Đối với đồ thị có trọng số: Thay vì đặt giá trị 1, ta đặt a[i][j] (và a[j][i] nếu là đồ thị vô hướng) bằng trọng số của cạnh.
- Bước 4: Nếu đồ thị có khuyên (cạnh nối một đỉnh với chính nó), đặt giá trị tương ứng trên đường chéo chính của ma trận (a[i][i]) bằng 1 hoặc trọng số của khuyên.
- Bước 5: Kiểm tra lại ma trận để đảm bảo tất cả các cạnh đã được biểu diễn chính xác.
Kết quả cuối cùng là một ma trận kề hoàn chỉnh, biểu diễn đầy đủ cấu trúc của đồ thị. Ma trận này có thể được sử dụng trong nhiều thuật toán xử lý đồ thị và phân tích cấu trúc.
Danh sách kề
Danh sách kề lưu trữ thông tin về các đỉnh và các cạnh lân cận của mỗi đỉnh trong một cấu trúc dữ liệu dạng danh sách. Mỗi phần tử trong danh sách kề đại diện cho một đỉnh, và giá trị của nó là danh sách các đỉnh lân cận với đỉnh đó.
Ưu điểm của danh sách kề
Danh sách kề chỉ lưu trữ thông tin về các cạnh thực sự tồn tại trong đồ thị, do đó nó có thể tiết kiệm bộ nhớ hơn so với ma trận kề, đặc biệt đối với đồ thị thưa (số lượng cạnh ít hơn so với số lượng đỉnh).
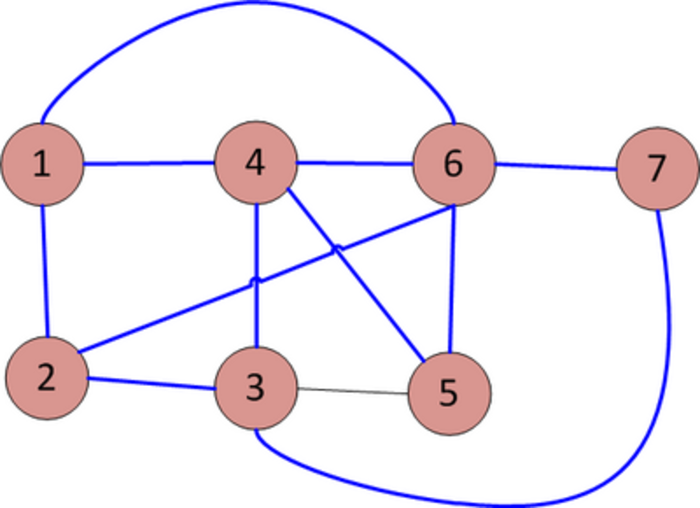
Việc truy cập danh sách lân cận của một đỉnh cụ thể trong danh sách kề có thể được thực hiện nhanh chóng bằng O(1).
Dễ dàng cập nhật: Việc thêm hoặc xóa cạnh trong đồ thị có thể được thực hiện dễ dàng bằng cách cập nhật danh sách kề tương ứng.
Nhược điểm của danh sách kề
Danh sách kề không cung cấp một cái nhìn tổng quan trực quan về cấu trúc của đồ thị như ma trận kề. Bên cạnh đó, việc tính toán danh sách kề từ ma trận kề có thể tốn thời gian, đặc biệt đối với đồ thị lớn.
Lời kết
Chúng tôi đã cung cấp cho bạn cái nhìn cụ thể nhất về ma trận kề. Nội dung này đóng vai trò quan trọng trong việc biểu diễn và nghiên cứu các đồ thị vô hướng. Nó cung cấp một cách thức trực quan và hiệu quả để lưu trữ thông tin về cấu trúc của đồ thị, giúp ích cho việc giải quyết nhiều bài toán liên quan đến đồ thị trong khoa học máy tính, toán học và các lĩnh vực liên quan.